Spin-magnon transmutation
Future green information and communication technologies should be highly integrated, fast, and energy efficient, while operating at room temperature. It is unlikely that conventional silicon-based CMOS technology will be able to meet these demands indefinitely as we move towards smaller devices. Of the many approaches taken to address this need, the field of spintronics strives to exploit the spin degree of freedom of the electron in order to develop alternatives to conventional electronics. In metals, spin currents heat the material through which they propagate just as charge currents do. In magnetic insulators, on the other hand, charge currents simply do not exist, while spin currents can still be transmitted with very little dissipation [1,2]. However, the efficiency of spin current actuation and detection remains an issue. Now, Christian Sandweg and colleagues at Technische Universität Kaiserslautern in Germany with collaborators at Tohoku University, Sendai, Japan, have demonstrated experimentally an unprecedented control of the pumping of electron spins by an insulating ferromagnet [3], which should encourage efforts towards a new class of electronics, in particular, information transmission systems.
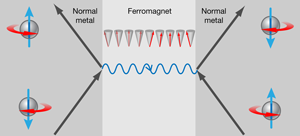
To explain this result we must consider what spin pumping really means. A mechanical pump transports fluid by means of a periodically varied mechanical action. In mesoscopic structures, electrons can be pumped one by one, by single-electron “turnstiles” [4]. If the approach to pump is by varying the system Hamiltonian instead of using an external bias, it is known as parametric pumping [5]. In contrast to a mechanical or charge pump, a pure spin pump transports angular momentum by moving an equal number of up and down spins in opposite directions. Such a device can be operated as a parametric quantum pump by the spin-dependent electron reflection at the interface between a nonmagnetic conductor and an excited ferromagnet, in which a quantum of the magnetization dynamics is emitted to generate a spin flip (see right interface in Fig. 1) [6]. Adiabatic quantum pumping of charge derived for mesoscopic systems [5] has never been unambiguously realized in such devices because, in real experiments, they are very difficult to disentangle from other competing effects. In contrast, the spin pumping by magnetization dynamics turned out in the last decade to be a robust and ubiquitous effect at ambient temperatures.
In addition to the spin-pumping effect, the interaction of electron spin with magnetic order produces a spin-transfer torque [7] that changes the direction of the magnetization. Spin pumping and spin-transfer torque are thermodynamically reciprocal processes [8], analogous to the Seebeck and Peltier effects in thermoelectrics. (The Seebeck effect refers to a voltage created by a temperature gradient, while the Peltier effect stands for the heat current introduced by an applied charge current. The associated material constants are related by the Kelvin-Onsager relation of reciprocity.) At the site of contact between a ferromagnet and a conductor, the spin current due to pumping is proportional to the rate of precession of the magnetic moment at the interface. For small particles, or while under a strong magnetic field, the dynamics of a ferromagnet at low energies is a coherent precession of the magnetization, where the ferromagnet behaves essentially like a single macrospin, for which all spins move as if they were one single giant spin. However, outside of such specialized situations, propagating spin waves emerge. Quanta of these finite wavelength excitations of the magnetic order parameter are called magnons (just like phonons are the quanta of elastic lattice vibrations), whose energies increase at short wavelengths. The magnons dispersion can be mapped experimentally by inelastic neutron scattering, or, in thin films, with inelastic (Brillouin) scattering of light. The latter technique has one drawback: since the wavelength of light is very long compared to the interatomic spacings, its linear momentum transfer is limited. The robustness of spin pumping with respect to the magnon wavelength, as shown in Ref. [3], overcomes even this limitation.
Spin pumping has been previously detected indirectly by increased damping due to the leakage of energy and angular momentum out of the ferromagnet into the conductor [9], spin back-flow induced voltages [10], and the inverse spin Hall effect (ISHE) [11], in which a spin current induces a transverse electromotive force in a normal metal with large spin-orbit interaction (usually platinum). In all these experiments, the motion of the ferromagnet has been a coherent macrospin precession. The balance between spin pumping and spin torque due to a thermodynamic nonequilibrium at an F|N interface also induces a net spin current that, when picked up by the ISHE, leads to a voltage or “spin Seebeck effect” [2]. In Ref. [3], microwaves are employed that selectively heat the metal of the ISHE detector, which also leads to a background spin Seebeck signal. The spin pumping used by Sandweg et al. [3] is not by monodomain magnetization precession, but by magnon wave packets generated in controlled narrow regions of reciprocal space by nonlinear microwave parametric pumping (not to be confused with spin pumping). This process excites spin waves at half the frequency of the incident microwaves, allowing for the generation of short-wavelength magnons. It then turns out that even short-wavelength magnons, inaccessible to other experimental techniques, generate a spin current that is detected by the ISHE. The comparatively reduced spin-pumping efficiency of the short-wavelength modes is attributed to the damping of the amplitude of the magnetization precession at the interfaces that lead to localization of particularly the short-wavelength magnons to the center of the magnetic film.
In conclusion, Sandweg et al. [3] have demonstrated that the detection of a spin-wave signal over a wide range of wave numbers can be accomplished by the spin-pumping mechanism. The material used for magnon generation and detection is the ferromagnet yttrium iron garnet (YIG), whose magnetization dynamics are hardly damped, making it a promising material for future spin-based electronics, where its wires could be used as interconnects between processing and data-storage modules. Obviously, the bandwidth of such a “spin-wave bus” [12] is a relevant figure of merit, which is why the result of Sandweg et al. is so promising. The use of the inverse spin Hall effect is not essential in the readout, but can, in principle, be replaced by other spin-current detection schemes, such as giant magnetoresistance, which scales more favorably when down-scaling the device dimensions, or unconventional (even insulating) ones based on magnetoelectric and magnetomechanical principles. While the present study concerns itself only with the spin-pumping readout, the actuation of spin waves by the spin-transfer torque [1] (see left interface in Fig. 1) is dictated by Onsager’s reciprocity principle, which means that the reverse operation should also be possible. Ultimately, the present results are a step forward in the development of, under ambient conditions, energy-efficient spin-based electronics that does not require itinerant charge carriers.
Acknowledgments
We acknowledge financial support from the Dutch FOM Foundation, EU-ICT-7 contract no. 257159 MACALO, DARPA, and NSF under Grant No. DMR-0840965.
References
- Y. Kajiwara et al., Nature 464, 262 (2010)
- K. Uchida et al., Nature Mater. 9, 894 (2010)
- C. W. Sandweg, Y. Kajiwara, A. V. Chumak, A. A. Serga, V. I. Vasyuchka, M. B. Jungfleisch, E. Saitoh, and B. Hillebrands, Phys. Rev. Lett. 106, 216601 (2011)
- D. V. Averin and K. K. Likharev, Mesoscopic Phenomena in Solids (Elsevier, Amsterdam, 1991)[Amazon][WorldCat]
- M. Büttiker, H. Thomas, and A Prêtre, Z. Phys. B Condens. Mat. 94, 133 (1994)
- Y. Tserkovnyak, A. Brataas, and G. E. W. Bauer, Phys. Rev. Lett. 88, 117601 (2002)
- J. C. Slonczewski, J. Magnet. Magnet. Mater. 159, L1 (1996)
- A. Brataas et al., in Spin Currents, edited by E. Saitoh, S. Maekawa, and T. Kimura (Cambridge University Press, Cambridge, to be published)
- S. Mizukami, Y. Ando, T. Miyazaki, Phys. Rev. B 66,104413 (2002)
- M. V. Costache, M. Sladkov, S. M. Watts, C. H. van der Wal, and B. J. van Wees, Phys. Rev. Lett. 97, 216603 (2006)
- E. Saitoh et al., Appl. Phys. Lett. 88, 182509 (2006)
- A. Khitun and K. L. Wang, arXiv:1012.4768