Bragging rights
X-ray scattering is a powerful tool to investigate the structure of materials. In particular, because x rays have a wavelength comparable to the spacing between ions in a solid, coherent scattering from a crystalline material leads to constructive interference in so-called “Bragg” directions, similar to the diffraction peaks of visible light reflected off a periodic grating. Crystallographers measure these Bragg angles to infer the structure of a solid, while biologists and chemists apply x-ray scattering to crystals of large molecules—most famously, to discover the double helix structure of DNA. Similarly, measurements of the scattering outside the Bragg peaks can reveal deviations from perfect order, or excitations.
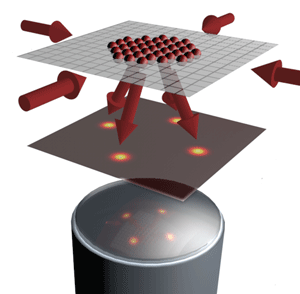
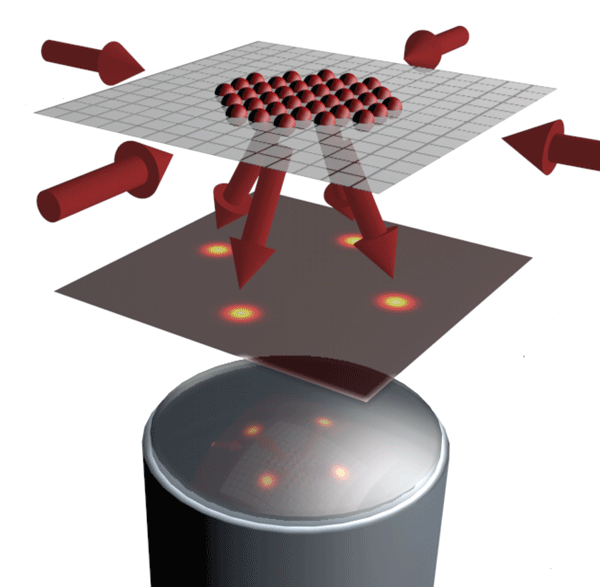
In many ways, neutral atoms moving in an optical lattice mimic the behavior of electrons moving in a conventional crystalline solid—only the period of the optical crystal is 1000 times longer than the ionic crystal, and of course atoms are more massive than electrons. For this reason, the energy and temperature scales relevant to neutral atomic systems are a billion times lower than their electronic counterparts, hence the need for “ultracold” conditions. In an article appearing in Physical Review Letters [1], Christof Weitenberg from the Max Planck Institute for Quantum Optics in Garching, Germany, and colleagues compare angle-resolved scattering and direct microscopy of ultracold atoms (Fig. 1). Their work is one of the most precisely controlled light-scattering experiments to date, and the first to apply crystallographic methods to neutral atoms prepared in an insulating phase. While recent work has demonstrated site-resolved images of such cold-atom lattices [2,3], in this new work, Weitenberg et al. shift the focus of their microscope away from the lattice and into the far field to measure the angular distribution of light scattered off such atoms. In this way, they are able to distinguish coherent from incoherent scattering, and demonstrate a detection method for magnetic ordering of atomic spins.
One might guess that microscopy would be the best way to learn about structure. Why then is angle-resolved scattering such a widespread technique? Exploring three-dimensional structure with microscopy is slow, because it requires examining atoms plane-by-plane or worse: scanning techniques acquire information point-by-point. Even if one had the patience for such a task, electron microscopy (such as transmission electron microscopy) cannot penetrate further than a few hundred nanometers into a material, because electrons scatter too strongly. X rays and neutrons scatter weakly, allowing them to penetrate into the bulk; but no good lenses are available for these probes. So structural determination of solids is nearly always done with far-field analysis of scattered x rays or neutrons.
In contrast, visible light scattering from neutral atoms can produce both angle-resolved data [4] and spatial images. In the last few years, a new generation of optical lattice experiments have implemented high-resolution microscopy [2,3,5,6]. In addition to requiring sophisticated optics, site-resolved imaging requires light to play the dual role of imaging probe and the coolant, keeping the atoms trapped while each scatters thousands of photons. The sample size is kept manageably small, to less than a thousand atoms. Although three-dimensional reconstruction is the goal of at least one group [5], others [2,3] work in a geometry where the atoms are restricted to move in a single plane.
The two-dimensional geometry of an isolated plane is also easier for crystallography. For a single-frequency laser beam, Bragg scattering from a three-dimensional crystal will only occur at specific incident angles. However, for a two-dimensional crystal, coherent diffraction occurs for any incident beam angle. Weitenberg et al. are able to use their laser-cooling light, which impinges on the atoms from several in-plane directions, for crystallographic analysis (see Fig. 1). Since this is the same light they use to image the atoms, no dedicated crystallography beam is required.
In fact, in a two-dimensional geometry, imaging and crystallography are not very different. Both involve the detection of scattered light. To take a crystallographic measurement, the angles of scattered beams are measured after they propagate away from the sample. Spatial imaging uses a lens (or several lenses) to reunite scattered beams at an image plane and interferometrically reconstruct the distribution of scattering sources. These two modes of data acquisition cannot be simultaneous, because ideal imaging erases all information about the direction in which light was scattered in the first place: all rays are brought into focus. Conversely, in the far field, the image is blurred out of recognition. This complementarity is simply the uncertainty principle applied to the position and wave vector of light.
In their new work, Weitenberg et al. take advantage of this complementarity and compare the results of their diffraction experiment to a real-space image of the atomic density. They find excellent agreement between the measured diffraction angles and what you would expect for the imaged positions of the atoms. They also observe that the peaks become more defined as the sample size grows, as it must for perfect crystalline order.
In their experiments, not all of the light scatters coherently into a diffraction peak, however. Instead, some of the light scatters incoherently, forming a diffuse background outside of the Bragg angles. Although one may be tempted to discard this background as a technical detail, doing so would “throw the baby out with the bath water.” Light that is scattered in ways other than perfect diffraction is informative: the scrambled phase can reveal the fingerprints of excitations or of limited long-range order. In Weitenberg et al.’s experiment, it turns out that 85% of the incident light is scattered incoherently. The reason is that the process of cooling the atoms changes the internal states of the atoms, which in turn scrambles the scattering phase randomly and independently at each site, destroying coherence. (Recall that cooling and scattering involve the same light.) When looking at microscopy images alone, these dynamics were not apparent because an image can be formed from either coherent or incoherent light.
As a further step, Weitenberg et al. implement a scheme to detect magnetic-spin ordering. Their imaging technique is not sensitive to the initial spin state of the atoms, for the same reason that incoherent light is being generated: the laser cooling beams scramble the internal states. However, they can convert the initial spin patterns into density patterns by removing one of two spin states with a resonant light “blast.” Although spontaneous generation of magnetic-spin ordering does not occur in their experiment, they imprint a stripe pattern using localized spin-flips [7] to demonstrate that diffraction could, in principle, detect such an ordering. The team observes a second Bragg peak in the scattered light, corresponding to the period of the stripe ordering.
Researchers without the advanced imaging system of the Max Planck team should be encouraged that Bragg-diffracted light passed the test of comparison to images. Analysis in situ reveals ordering and structure lost in the time-of-flight analysis used by most cold-atom experiments. But Weitenberg et al. did not learn anything about lattice occupancy from diffracted light that they didn’t already know from microscopy images. So has microscopy put cold-atom crystallography out of business?
Not quite. Observing scattered light in the far field can trump imaging in a number of circumstances. First, as discussed above, for large or three-dimensional samples, crystallography can obtain information about the bulk, where imaging may be impractical. Second, one can acquire information with less than one photon per atom, thus probing the system nondestructively and quickly. The Max Planck team acquires light for several tenths of a second, whereas earlier work using Bragg scattering observed average motional dynamics with microsecond resolution [8]. Depending on the physics under investigation, one may not need to know exactly which sites are occupied, so complete imaging is not necessary. Photon-efficient probing may also be the best option when scattering thousands of photons per atom is not possible, for instance, in more shallow lattices, or when probing molecules with open transitions. Of course, the challenge of “photon efficiency” is that it produces a small signal for samples of only a few hundred atoms, without further tricks [9].
A third advantage of angle-resolved intensity measurements is that scattering can probe excitations. The response of a system to excitations reveals physics (such as pairing) that leaves no direct trace in images of lattice occupancy. So far, experiments have detected optical excitations excitations by looking at the recoiling atoms instead of the scattered photons [10]. Such an approach creates the excitation nondestructively, but then destroys the sample during detection. Weitenberg et al.’s results encourage us to dream of yet another generation of experiments, in which quantum many-body physics, such as magnetic ordering, is probed nondestructively with just a few scattered photons.
Acknowledgments
The author thanks David McKay, Ken Burch, and Arun Paramekanti for discussions.
References
- C. Weitenberg, P. Schauß, T. Fukuhara, M. Cheneau, M. Endres, I. Bloch, and S. Kuhr, Phys. Rev. Lett. 106, 215301 (2011)
- W. S. Bakr et al., Nature 462, 74 (2009); Science 329, 547 (2010)
- J. Sherson et al., Nature 467, 68 (2010)
- G. Birkl, M. Gatzke, I. H. Deutsch, S. L. Rolston, and W. D. Phillips, Phys. Rev. Lett. 75, 2823 (1995); M. Weidemüller, A. Hemmerich, A. Görlitz, T. Esslinger, and T. W. Hänsch, 75, 4583 (1995)
- K. D. Nelson et al., Nature Phys. 3, 556 (2007); D. S. Weiss et al., Phys. Rev. A 70, 040302 (2004)
- T. Gericke, P. Würtz, D. Reitz, T. Langen, and H. Ott, Nature Phys. 4, 949 (2008)
- C. Weitenberg et al., Nature 471, 319 (2011)
- G. Raithel, G. Birkl, W. D. Phillips, and S. L. Rolston, Phys. Rev. Lett. 78, 2928 (1997); P. Rudy, R. Ejnisman, and N. P. Bigelow, 78, 4906 (1997); A. Görlitz, M. Weidemüller, T. W. Hänsch, and A. Hemmerich, 78, 2096 (1997)
- I. B. Mekhov, C. Maschler, and H. Ritsch, Nature Phys. 3, 319 (2007); W. Chen, D. Meiser, and P. Meystre, Phys. Rev. A 75, 023812 (2007); J. Ruostekoski, C. J. Foot, and A. B. Deb, Phys. Rev. Lett. 103, 170404 (2009)
- For instance, J. Steinhauer, R. Ozeri, N. Katz, and N. Davidson, Phys. Rev. Lett. 88, 120407 (2002)