Changing repulsion into attraction with the quantum Hippy Hippy Shake
In a paper in Physical Review Letters [1], Naoto Tsuji, Takashi Oka, and Hideo Aoki, all at the University of Tokyo, and Philipp Werner at ETH, Zurich, show that a system of electrons that initially repel each other when at equilibrium (described by a temperature T) can be changed to one where repulsive interactions are replaced by attractive ones. This change occurs when the system is driven by an electric field that is constant in space but oscillates rapidly in time. The phenomenon arises from the generic behavior of correlated quantum particles that are driven in an oscillatory way on a periodic lattice.
Correlated motion occurs when the movement of one particle depends on the behavior of others. The concept is familiar to children who play with puzzles like the famous “fifteen” puzzle involving moving 15 pieces in a 4×4 square with one empty space. The aim is to organize the squares in a particular order, but one needs to interchange pieces without destroying the order that has already been established. A more complicated example is the Rubik’s cube; same principle but in three dimensions.
Quantum particles with strong particle-particle interactions exhibit correlated motion. Much of the framework for solving these problems for a system in equilibrium at a given temperature comes from work done in the 1940s and 1950s, culminating in the classic text by Abrikosov, Gorkov, and Dzyaloshinskii [2]. In the 1960s, new developments by Baym and Kadanoff [3] and by Keldysh [4] showed how to extend these formal developments to solve the nonequilibrium many-body problem. It turned out that the resulting equations were too complex to use except in some approximate fashion. This impasse lingered for many years.
In the 1990s it became possible to study experimental systems in nonequilibrium, typically in semiconductor systems. This is when Bloch oscillations were observed in superlattice structures [5] and nonequilibrium transport was measured in quantum dots [6]. More recently, in the past decade, we have seen frenetic activity in nonequilibrium experiments, ranging from pump-probe photoemission or reflectivity experiments [7], to virtually all experiments in ultracold atomic systems trapped in optical lattices [8]. There have been experiments performed in ion traps where a simple quantum state slowly evolves into a complicated correlated one with directly measurable properties [9]—Feynman’s analog quantum computer [10].
Theory has lagged behind experiment in this recent revolution, especially for quantum problems which involve fermions (such as electrons). This is because the most successful numerical techniques like quantum Monte Carlo simulations often develop errors due to what is called the fermion sign problem, which makes it impossible to perform calculations at low temperatures. Progress has, however, been made in one-dimensional problems, where a technique that systematically solves increasingly larger systems using matrix diagonalization methods has been employed to describe the nonequilibrium evolution of many different quantum states [11]. In 2006, dynamical mean-field theory, an extremely useful tool for solving the equilibrium many-body problem starting from the limit of large numbers of spatial dimensions, was generalized to solve nonequilibrium problems [12]. This technique has subsequently been applied to a large number of different problems.
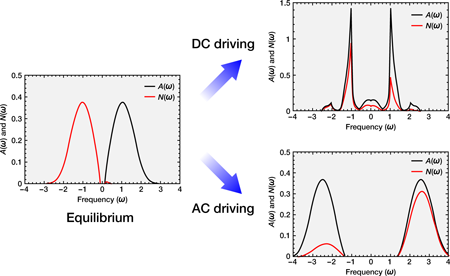
The work of Tsuji et al. is within the framework of the nonequilibrium dynamical mean-field theory, but comes with some surprising results. They find that the main effect of the driving field is to renormalize the energy scale for motion between nearest-neighbor sites on the lattice (which is called the hopping integral). When this hopping integral changes sign, they find that the system can be described by an effective negative temperature, or equivalently, by a positive temperature but with the repulsive interactions changed to attractive. What is most surprising is that a nonequilibrium system can be described by such a simple picture involving only a change of scale in the energy and possibly a change of interactions from repulsive to attractive. Most nonequilibrium problems are much more complicated to describe.
Take for example the problem of Bloch oscillations [13]. A constant electric field accelerates noninteracting electrons on a periodic lattice. But an electron cannot move too far before its wave vector reaches the boundary of the Brillouin zone and Bragg reflects it to an opposite side. The velocity of the electron changes sign during this reflection. Changing directions with each reflection, the electron eventually moves in a periodic fashion. The frequency of this motion is called the Bloch frequency, which is proportional to the magnitude of the electric field. The quantum mechanical states are completely rearranged by this motion. Instead of a continuous band of eigenstates, the system has a density of states given by a series of weighted delta functions separated by the Bloch frequency. The occupation of these states changes periodically. If interactions are added to the system, then the delta functions broaden, but also split into Mott-Hubbard subbands, with a splitting of the peaks of the subbands given by the strength of the electron-electron interaction. This is an example of a system that cannot be described by a simple rescaling of energy scales.
A very different picture arises in the case of noninteracting electrons driven by an electric field that oscillates with a high frequency but remains uniform in space. To a very good approximation, the main effect of the driving field is to multiply the hopping integral by a factor that can be either positive or negative. If the factor equals zero, then the particles cannot hop to nearest-neighbor sites and the system exhibits dynamical localization [14]. If the hopping integral changes sign, then the band inverts, and the states around zero momentum (the lowest energy states before the field is turned on) become the highest energy states. For large frequencies, electrons with definite momentum oscillate rapidly about their momentum values, but do not evolve across the Brillouin zone like they do for a constant field. Hence the highest energy states of the system are occupied; we have a negative temperature, or a population inversion. We can describe this population inversion as an equilibrium distribution at positive temperature of a system described by the negative Hamiltonian - H.
Tsuji et al. focus on the interacting case. If the particle-particle interactions are not modified by the driving field (except by the overall renormalization of energy scales), inverting the sign of all of the energies that describe the system in an equilibrium distribution with a positive temperature changes the sign of the interaction. In other words, the driving field changes the system from a repulsive to an attractive one. Not too surprisingly, the authors find that whenever the oscillating field is turned on rapidly, this effective temperature of the system increases in magnitude. A schematic is given in Fig. 1.
Using a nonequilibrium quantum Monte Carlo simulation, Tsuji et al. show that this simple picture describes their system quite accurately. They examine the system by suddenly turning on a high-frequency electric field. They compare this to what happens when they suddenly change the interaction strength. While there are often additional oscillations in the system driven by the electric field, the time-averaged quantities (averaged over the period of the electric field) appear to be very close to the results one gets by rapidly changing the value of the interaction.
Tsuji et al. argue that these nonequilibrium configurations will remain stable if the system is isolated from the environment because the energy is conserved, and hence cannot relax. This point of view is clearer for the attractive model, which is described by an effective equilibrium distribution. Relaxation can occur if the system is coupled to an environment that allows for energy exchange. The authors argue that it might be easiest to see these effects in ultracold atomic systems trapped in optical lattices. One needs to understand the effect of the trap on this phenomenon, as it will switch signs from positive to negative curvature leading to additional effects. In any case, the future is bright for new insights into the nonequilibrium many-body problem.
Acknowledgments
I acknowledge support of the ARO grant W 911NF 0710576 with funds from the DARPA OLE Program, the AFOSR MURI program grant FA 9559- 09- 1- 0617, the NSF under grant number DMR- 1006605, the INDO-US Science and Technology Forum JC- 18- 2009 Ultracold atoms, and the McDevitt endowment trust at Georgetown University.
References
- N. Tsuji, T. Oka, P. Werner, and H. Aoki, Phys. Rev. Lett. 106, 236401 (2011)
- A. A. Abrikosov, L. P. Gorkov, and I. Y. Dzyaloshinskii, Quantum field theoretical methods in statistical physics, International series of monographs in natural philosophy Vol. 4 (Pergamon Press, Oxford, 1965)
- L. P. Kadanoff and G. Baym, Quantum Statistical Mechanics (W. A. Benjamin, Inc., New York, 1962)[Amazon][WorldCat]
- L. V. Keldysh, J. Exptl. Theor. Phys. 47, 1515 (1964); Sov. Phys. JETP 20, 1018 (1965)
- C. Waschke, H. G. Roskos, R. Schwedler, K. Leo, H. Kurz, and Klaus Köhler, Phys. Rev. Lett. 70, 3319 (1993)
- D. Goldhaber-Gordon, Hadas Shtrikman, D. Mahalu, David Abusch-Magder, and U. Meirav, M. A. Kastner, Nature, 391, 156 (1998)
- L. Perfetti et al., Phys. Rev. Lett. 97, 067402 (2006); F. Schmitt et al., Science 321, 1649 (2008)
- See for example, I. Bloch, J. Dalibard, and W. Zwerger, Rev. Mod. Phys. 80, 885 (2008)
- K. Kim et al., Nature, 465,590 (2010)
- R. Feynman, Int. J. Theor. Phys. 21, 467 (1982)
- See, for example, U. Schollwöck, Rev. Mod. Phys. 77, 259 (2005)
- J. K. Freericks, V. M. Turkowski, and V. Zlatić, Phys. Rev. Lett. 97, 266408 (2006)
- F. Bloch, Z. Phys. 52, 555 (1928); C. Zener, Proc. R. Soc. London A 145, 523 (1934)
- D. H. Dunlap and V. M. Kenkre, Phys. Rev. B 34, 3625 (1986); M. Holthaus, Phys. Rev. Lett. 69, 351 (1992)