Holes in the stream

Giovanni Vignale

Viewpoint

Holes in the stream

Department of Physics and Astronomy, University of Missouri, Columbia, Missouri 65211, USA

June 13, 2011• Physics 4, 48

Measurement of the Coulomb drag correlation in a two-dimensional electron gas provides a quantitative explanation for the movement of electron-hole packets opposite to the expected direction.

Figure caption — **Figure 1:** Schematic depiction of electron-hole packets in a two-dimensional electron gas (2DEG). (a) In the textbook description, the electron-hole packets drift in the direction of the applied field, with the holes leading the way. (b) In a high mobility 2DEG, the Coulomb drag correlation (indicated schematically by the wavy line) transfers momentum between electron and holes. The coupling creates an effective “drag field” on the holes, which reverses the drift so that the packets move in the direction opposite to the applied field. (The small separation between electron and hole density maxima is barely visible on the scale of this graph)

The behavior of coupled electron-hole packets is crucial to the properties of certain semiconductor devices, such as some spintronic systems that rely on spin currents carried by polarized electron-hole packets [1]. But the motion of these packets in an electric field, known as ambipolar transport because the electrons and holes move in a coherent way, does not always follow the predictions of standard theory [2]—in some circumstances, they move in the opposite direction to what is expected [3]. Although the underlying reason for this behavior has been known for some time, Luyi Yang at Lawrence Berkeley National Laboratory and colleagues have measured a key quantity characterizing the nonstandard motion [4]. The new work, which appears in Physical Review Letters, should make possible better modeling and design of ambipolar transport in devices.

Laser light with energy larger than the band gap of a semiconductor quantum well that hosts, say, a two-dimensional electron gas (2DEG), will excite additional electrons in the conduction band and holes in the valence band. If the laser intensity is spatially nonuniform, these additional electrons and holes concentrate where the laser intensity is higher; if the laser is focused on a single spot, they form an electron-hole packet. Once the laser is turned off, the electrons and holes begin to recombine, but the recombination time is sufficiently long to allow experimentalists to monitor the packet’s evolution. The packet undergoes diffusion, spreading at a rate controlled by the so-called ambipolar diffusion constant $D_{a}$ , a weighted average of the diffusion constants of electrons $D_{e}$ and holes $D_{h}$ [2]:

where $σ_{e}$ and $σ_{h}$ , the Drude conductivities of electrons and holes, are proportional to the densities of electrons and holes. In an electric field $E$ , the packet will drift at a velocity $v_{p} = μ_{a} E$ , where the ambipolar mobility is

$μ_{e}$ and $μ_{h}$ being the electron and hole mobilities, respectively. The drift velocity of the packet will, in general, differ from the drift velocity of the underlying majority carriers: it is the velocity of propagation of a disturbance on the sea of majority carriers. If the electrons are in an overwhelming majority, as is often true in practice, $σ_{e} ≫ σ_{h}$ and therefore $D_{a} ≅ D_{h}$ and $μ_{a} ≅ μ_{h}$ . The electron-hole packet should then drift in the direction of the electric field, opposite to the direction in which electrons drift, with a velocity determined by the mobility of the holes.

Ambipolar mobility has long been understood in terms of dielectric screening—the Coulomb correlation that tends to suppress any spatial charge imbalance in a high-mobility electron gas. An electric field causes the electrons and the holes in a packet to start drifting in opposite directions, but the Coulomb attraction between the electrons and the holes prevents them separating beyond a critical distance $\bar{μ} E τ_{d}$ , where $\bar{μ}$ is the average carrier mobility and $τ_{d}$ is the dielectric relaxation time, which is usually very short in a high-mobility semiconductor. Once this separation is reached, the drifting holes lead the packet, pulling up and discarding background electrons as they go to maintain charge neutrality. In brief, the packet—regarded as a disturbance of the 2DEG—is located where the holes are, and goes where the holes go.

As early as the 1980s, however, it became clear that this simple picture could not be the whole story. In 1986, Höpfel et al. [3] reported that an electron-hole packet injected in a high mobility $GaAs$ quantum well would drift in the direction of the majority rather than the minority carriers. This seems very strange: What could persuade the positively charged holes to drift against the direction of the electric field? Höpfel et al. proposed an explanation that hinges on another correlation between electrons and holes, the Coulomb drag correlation. When electrons and holes drift with different average velocities—as they do when an electron-hole packet moves through an electron gas—the density fluctuations of the two species of carriers tend to interlock. This causes a phenomenon akin to friction, by which momentum transfer from one species to the other reduces their velocity difference. This phenomenon has long been studied in bilayer systems [5], not only for its intrinsic interest (quantitative tests of many-body theories of the 2DEG, diagnostics of phase transitions), but also as a possible way of coupling devices. In the case of bilayer systems, however, the electron-hole interaction is rather small and the effect is correspondingly weak.

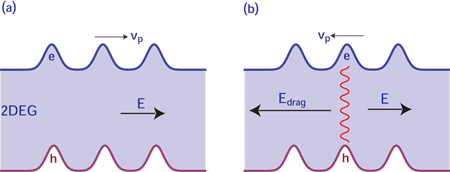
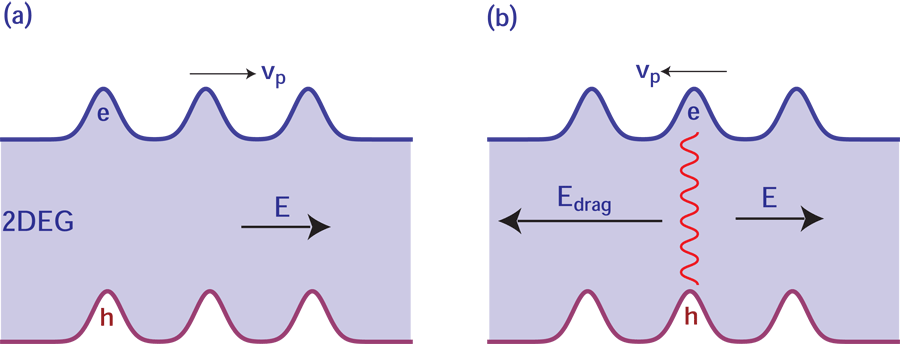
In the Höpfel et al. experiment, on the other hand, electrons and holes coexist in the same layer. Momentum transfer between electrons and holes acts as an effective electric field that opposes the external field, and can force the holes to drift in a direction opposite to their natural inclination, or, in other words, to go with the electron flow [see Fig. 1(b)]. The drag field on the holes is

where $j_{e}$ is the electron current density, $ρ_{e}$ is the usual electron resistivity, and $ρ_{e h}$ is the electron-hole transresistivity, which relates the field acting on one carrier species to the current of the other. A key point is that $ρ_{e h}$ has an intrinsic origin (the Coulomb drag correlation), while $ρ_{e}$ is primarily controlled by extrinsic impurity scattering and can, in principle, be made arbitrarily small. The drag field can therefore overcome the external field if $ρ_{e h} > ρ_{e}$ , i.e., if the electron mobility of the 2DEG is sufficiently high.

Ironically, the key quantity $ρ_{e h}$ has been thoroughly studied in bilayer systems [5] but never before in a single-layer system. The reason is that bilayer measurements relied on the ability to separately probe the two layers—a possibility that does not exist here. Yang et al. [4] have now found a way to do the single-layer measurement by using a completely different experimental technique. Rather than creating a single electron-hole packet, Yang and coauthors create an electron-hole density modulation by superimposing on the surface of a 2DEG two linearly polarized laser beams coming from different directions [6]. Interference between the laser beams creates a standing wave, and electron-hole packets form under its maxima [see Fig. 1(a)]. The resulting electron-hole density modulation then serves as a diffraction grating for another laser beam, acting as a probe. From the intensity of the diffraction pattern the experimenters can determine the amplitude of the electron-hole density modulation. Naturally, this amplitude decays after the pump laser beams are switched off; this is why Yang et al. call the technique transient grating spectroscopy. By measuring the decay rate of the electron-hole density modulation as a function of its own wavelength (the latter is varied by changing the angle between the beams), the experimenters extract both the electron-hole recombination time and the ambipolar diffusion constant. Finally, by measuring the phase shift of the diffracted wave relative to a reference wave, they are able to determine the drift velocity of the grating, and hence the value of the ambipolar mobility.

Yang et al. have developed a simple quantitative model that expresses $D_{a}$ and $μ_{a}$ in terms of the electron and hole mobilities and the electron-hole transresistance for different 2DEG densities and laser intensity levels. From their formulas the hole transresistivity can be extracted. In contrast to the bilayer case, in which $ρ_{e h}$ is smaller than $ρ_{e}$ , here $ρ_{e h}$ is larger than $ρ_{e}$ throughout the range of temperatures explored in the experiment, so that ambipolar mobility is always negative. At low temperature, $ρ_{e} ≪ ρ_{e h}$ and the ambipolar mobility approaches the electronic mobility: the relative velocity between the packet and the background electrons is effectively zero. At higher temperature, the electronic resistance increases more rapidly than the electron-hole transresistivity: as $ρ_{e h} / ρ_{e}$ approaches $1$ , the packet mobility approaches the hole mobility in absolute value, but still has a negative sign. Only for $ρ_{e h} ≪ ρ_{e}$ is the “textbook result” recovered. Remarkably, the measured transresistivity is in good quantitative agreement with a simple microscopic calculation of momentum transfer rate between electrons and holes.

Besides filling an obvious gap in our understanding of the impact of Coulomb correlations on electron-hole transport, the experimental techniques described by Yang et al. open up a number of exciting possibilities. Changing the polarization of the laser pumps from linear to circular would generate spin gratings whose mobility could be studied in experiments similar to the ones that led to the first observation of spin Coulomb drag [7,8]. The spin grating can be made hole-free by going to times longer than the electron-hole recombination time, but then the spin orbit interaction, which is very significant in, say, a $[100]$ $GaAs$ quantum well, becomes important. It will then be possible to study the behavior of the spin grating mobility near special wavelengths, where an extremely long-lived helical state has been predicted [9] and subsequently observed [10]. This will deepen our understanding of these intriguing new states of electronic matter. On a more practical level, the techniques developed in this paper will be useful for a better characterization of carrier transport in spintronic devices.

Acknowledgments

This work was supported by DOE under Grant No. DE-FG02-05ER46203. I thank M. E. Flatté for a useful discussion.

References

M. E. Flatté in Manipulating Quantum Coherence in Solid State Systems, NATO Science Series II: Mathematics, Physics, and Chemistry, edited by M. E. Flatté and I. Tifrea (Springer, Dordrecht, 2007)[Amazon][WorldCat]
Semiconductors, edited by R. A. Smith (Cambridge University Press, New York, 1978)[Amazon][WorldCat]
R. A. Höpfel, J. Shah, P. A. Wolff, and A. C. Gossard, Phys. Rev. Lett. 56, 2736 (1986)
L. Yang, J. D. Koralek, J. Orenstein, D. R. Tibbetts, J. L. Reno, and M. P. Lilly, Phys. Rev. Lett. 106, 247401 (2011)
For a review, see A. G. Rojo, J. Phys. Condens. Matter 11, R31 (1999)
A. R. Cameron, P. Riblet, and A. Miller, Phys. Rev. Lett. 76, 4793 (1996)
G. Vignale in Manipulating Quantum Coherence in Solid State Systems, NATO Science Series II: Mathematics, Physics, and Chemistry, edited by M. E. Flatté and I. Tifrea (Springer, Dordrecht, 2007)[Amazon][WorldCat]
C. P. Weber, N. Gedik, J. E. Moore, J. Orenstein, J. Stephens, and D. D. Awschalom, Nature 437, 1330 (2005)
B. A. Bernevig, J. Orenstein, and S.-C. Zhang, Phys. Rev. Lett. 97, 236601 (2006)
J. D. Koralek et al., Nature 458, 610 (2009)

About the Author

Giovanni Vignale is Curators’ Professor of Physics at the University of Missouri-Columbia. After graduating from the Scuola Normale Superiore in Pisa in 1979 and gaining his Ph.D. at Northwestern University in 1984, he carried out research at the Max-Planck-Institute for Solid State Research in Stuttgart, Germany, and Oak Ridge National Laboratory. He became a Fellow of the American Physical Society in 1997. Professor Vignale’s main areas of research are many-body theory and density-functional theory. He is the author of two books, Quantum Theory of the Electron Liquid and The Beautiful Invisible and has published almost 200 papers.