Not your usual NMR

Edmund Myers

Viewpoint

Not your usual NMR

Department of Physics, Florida State University, Tallahassee, FL 32306-4350, USA

June 20, 2011• Physics 4, 49

Researchers have detected spin flips of a single proton, a first step toward precision measurements of the antiproton’s spin magnetic moment.

Figure caption — **Figure 1:** Simplified geometry of the Penning trap used by Ulmer *et al.* The proton $p$ oscillates axially along the magnetic field lines due to the electric potentials applied to the ring electrodes (here, labeled + and − according to their polarity). A superconducting solenoid (not shown) that surrounds the trap produces a uniform magnetic field. The (weak) radio-frequency magnetic field $B_{rf}$ causes the proton spin to flip. The interaction between the proton’s spin magnetic moment and the inhomogeneous magnetic field produced by the center electrode (made of ferromagnetic material), results in a tiny, but detectable, change in the proton’s axial oscillation frequency.

The CPT theorem implies, except for the sign of various properties such as charge, a particle and its antiparticle should be absolutely identical. The theorem is an essentially inviolable tenet of quantum field theory, and one that follows from the assumption that physics is the same in all inertial frames. The CPT theorem has been tested with baryons—composite particles made up of quarks bound by the strong interaction—by using a Penning trap to compare the masses of the proton and the antiproton to a precision better than one part in $10^{10}$ [1]. An important further test would be an accurate comparison of their intrinsic (spin) magnetic moments, which should also be identical, except for sign. A collaboration between researchers at several institutions in Germany (Ulmer et al.) has now taken a major step toward this goal. Writing in Physical Review Letters, they report the observation of spin flips of a single proton confined to a Penning trap [2].

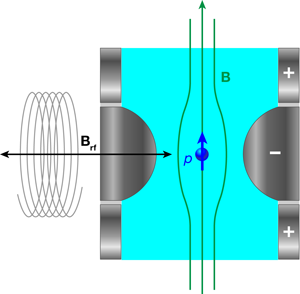
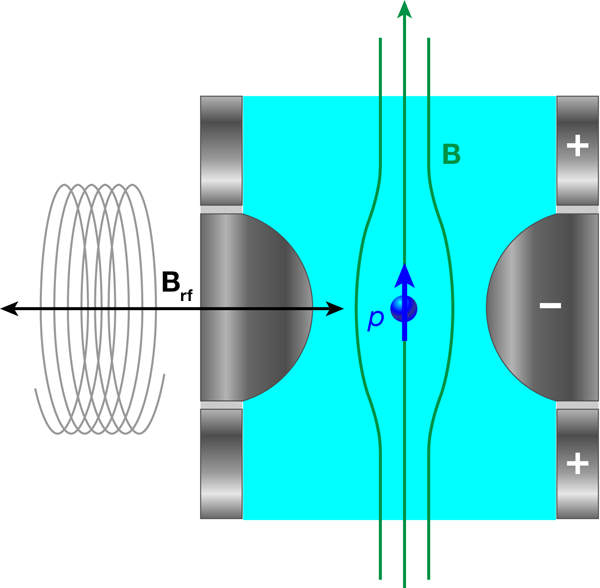
A Penning trap confines a charged particle, in ultrahigh vacuum, using a uniform magnetic field, which causes the particle to undergo a circular cyclotron motion; and an electrostatic potential, which causes the particle to oscillate along the axis of the trap, parallel to the magnetic field (Fig.1). The magnetic moment of the particle, expressed as the dimensionless quantity known as the $g$ factor, can be measured very precisely in this setup because it is the ratio of two frequencies: the Larmor spin-precession frequency, which is the frequency of the (weak) oscillating magnetic field needed to flip the proton’s spin direction with respect to the magnetic field in the trap, and the frequency of the particle’s cyclotron motion. In essence, the cyclotron frequency measures the magnetic field. Although there are other methods for measuring the magnetic moment of the proton—after all, Larmor precession is the basis of nuclear magnetic resonance (NMR)—none of these can be readily applied to the antiproton. Using a Penning trap, the antiproton magnetic moment could be measured to better than one part in $10^{9}$ , a millionfold improvement over existing values [3].

In the 1970s and 1980s, Hans Dehmelt and colleagues at the University of Washington, Seattle, made many seminal developments in precision Penning trap techniques with single particles [4,5]. This work culminated in a precise measurement of the magnetic moment of the electron, which provided the most precise test of quantum electrodynamics theory and the most precise value for the fine structure constant $α$ . (These results have now been superseded, but only in the last few years [6].) Dehmelt and colleagues also compared the magnetic moments of the electron and its antiparticle, the positron, with an uncertainty of only two parts in $10^{12}$ , yielding a precise test of the CPT theorem for leptons [5].

In a Penning trap, the frequencies of the cyclotron and axial motions of a charged particle can be measured by detecting, using tuned circuits and cryogenic preamplifiers, the oscillating image charges induced in the trap electrodes. Though the amplitudes of these motions are small, both types of motion can be classical and involve many energy quanta. But how does one detect the single-quantum flip of a single spin? (In conventional magnetic resonance experiments, EPR and NMR, the sample is macroscopic and contains many spins.) To solve this problem, Dehmelt developed what he called the “continuous Stern-Gerlach (CSG) effect.” If the magnetic field is deliberately made nonuniform—usually with a quadratic variation—the extra force, from the interaction of the magnetic moment with the magnetic field gradient, changes the frequency of the axial motion by a small amount, and this frequency shift depends on the direction of the electron spin. Hence a spin flip can be detected, elegantly and nondestructively, by detecting the small change in the axial frequency. The problem with extending this CSG technique from an electron to a proton is that the magnetic moment of the proton is $658$ times smaller than that of the electron. The tiny shift in axial frequency due to a proton spin flip is thus very hard to detect.

In order to give themselves the best chance to measure this shift, Ulmer and colleagues developed a special miniature Penning trap in which the entire center electrode was made of ferromagnetic material to produce a very strong quadratic field gradient. In fact, at the trap center, this ferromagnetic ring reduced the strength of the uniform magnetic field, produced by a superconducting solenoid that surrounds the trap, from $1.89$ to $1.17$ tesla. Even so, the predicted change in axial frequency due to the proton spin flip was only $0.19 Hz$ , and that had to be measured on top of a total axial frequency of $674 kHz$ !

Unfortunately, this was the level at which the axial frequency drifted and fluctuated, despite the team’s use of extremely stable voltage sources and efforts to reduce the introduction of external noise. In the reported work, they obtained their best sensitivity to changes in the axial frequency using a signal averaging time of $80$ seconds. The resulting root-mean-square fluctuation between successive measurements was then about $0.15 Hz$ . This level of stability was not quite enough to unambiguously detect the $0.19 Hz$ shift due to a single spin flip.

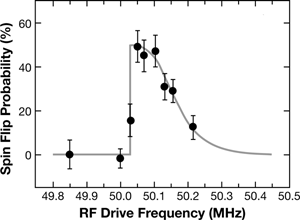
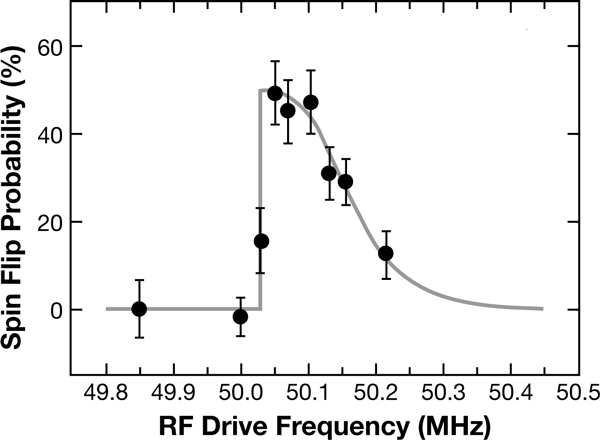
However, by repeatedly exposing the proton to radio frequency (rf) at the Larmor frequency, they could reproducibly detect an increase in fluctuations in the axial frequency. Furthermore, by varying the frequency of the rf, and using the increase in axial frequency fluctuations as their signal, they could map out a spin-flip resonance. This resonance, which is shown in (Fig.2), has a rather broad, asymmetric exponential shape. This corresponds to the Boltzmann distribution of the amplitudes of the proton’s axial motion (in thermal equilibrium with the detection circuit), combined with the strong magnetic field gradient. By fitting the line shape, they could measure the Larmor frequency (at the trap center) to a precision of $0.02 %$ . Their result agreed with the value expected from the measurement of the magnetic field using the proton’s cyclotron frequency—a convincing demonstration that they had indeed observed spin flips of a single proton.

But this is certainly not the end of the story. In order to achieve the goal of a Penning trap measurement of the $g$ factor of the proton (and antiproton) at a precision below one part in $10^{9}$ , the German collaboration, as do their competition from Harvard [7], plan to induce the spin flips in a Penning trap with a uniform magnetic field—which will give a much narrower resonance—and then transfer the proton to a second trap with a strong field gradient, to detect the spin flip. (The traps are adjacent and share the strong magnetic field so the spin direction is unchanged on transfer.) This scheme, which some of the authors have already successfully implemented on measurements of the (electronic) magnetic moments of hydrogenlike ions [8], requires sufficient stability of the axial frequency to unambiguously detect a single spin flip. Once an accurate measurement of the $g$ factor of the proton has been demonstrated, a similar Penning trap setup, connected to the Antiproton Decelerator at CERN, in Geneva, Switzerland, will be used for the antiproton measurement.

Interestingly, Ulmer et al. indicate that the limitation in the stability of the ion’s axial frequency was not due to instability in the voltage that confines the proton. Instead, they believe the instability was due to fluctuations in the cyclotron energy: the magnetic moment associated with the cyclotron motion also causes a shift in the axial frequency, and a unit change in cyclotron quantum number shifts the axial frequency by $0.068 Hz$ . In a study to be reported elsewhere, they found that the observed residual fluctuations in axial frequency were consistent with fluctuations in the cyclotron energy at an average rate of one quantum jump every $20$ seconds. Besides the immediate goal of measuring the antiproton $g$ factor to test CPT, an understanding of how the radial motion is being heated could have implications for research on quantum information processing using trapped electrons and ions.

References

G. Gabrielse, A. Khabbaz, D. S. Hall, C. Heimann, H. Kalinowsky, and W. Jhe, Phys. Rev. Lett. 82, 3198 (1999)
S. Ulmer, C. C. Rodegheri, K. Blaum, H. Kracke, A. Mooser, W. Quint, and J. Walz, Phys. Rev. Lett. 106, 253001 (2011)
K. Nakamura et al. (Particle Data Group), J. Phys. G 37, 075021 (2010)
L. S. Brown and G. Gabrielse, Rev. Mod. Phys. 58, 233 (1986)
R. S. Van Dyck, Jr., P. B. Schwinberg, and H. G. Dehmelt, Phys. Rev. Lett. 59, 26 (1987)
D. Hanneke, S. Fogwell, and G. Gabrielse, Phys. Rev. Lett. 100, 120801 (2008)
N. Guise, J. DiSciacca, and G. Gabrielse, Phys. Rev. Lett. 104, 143001 (2010)
H. Häffner, T. Beier, N. Hermanspahn, H.-J. Kluge, W. Quint, S. Stahl, J. Verdú, and G. Werth, Phys. Rev. Lett. 85, 5308 (2000)

About the Author

Edmund Myers is a Research Professor and Distinguished University Scholar in the Department of Physics at Florida State University. He obtained his D.Phil. at the University of Oxford, England, and carried out postdoctoral work at Rutgers University and AT&T Bell Labs. His experimental AMO research group measures atomic masses with a Penning trap.