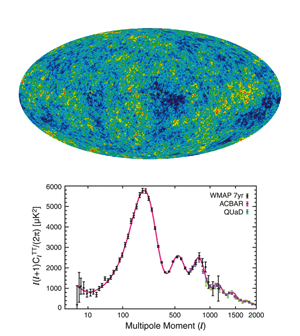
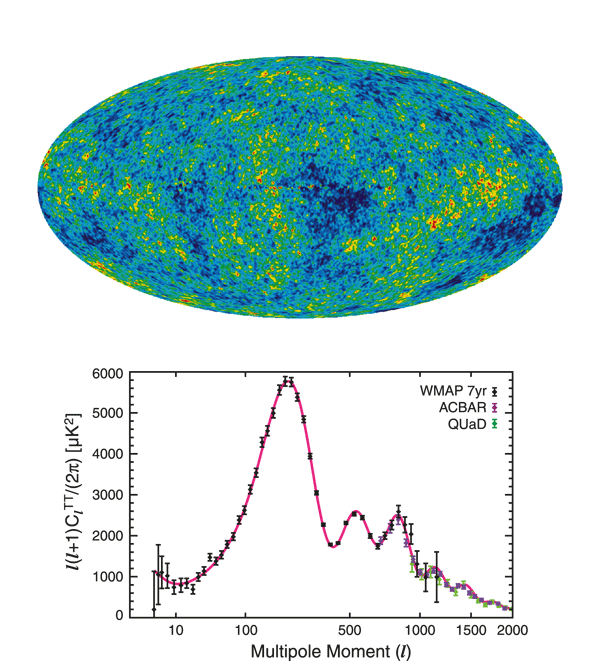
A distorted view of the early universe

Stephen Boughn

Viewpoint

A distorted view of the early universe

Department of Physics and Astronomy, Haverford College, Haverford, PA 19041, USA

July 5, 2011• Physics 4, 53

Gravitational lensing distorts maps of the cosmic microwave background, providing yet another way of probing the matter and energy content of the universe.

Figure caption — **Figure 1:** (Top) A sky map of the universe $13.7$ billion years ago. The different colors correspond to temperature fluctuations ( $+ / - 200$ milliKelvin) in the cosmic microwave background. (Bottom) A convenient way to analyze this data is to take an angular spherical harmonic transform. The resulting temperature power spectrum is plotted against the order of the spherical harmonic. (The legend indicates the different collaborations that contributed to the data.)

Two of the most powerful methods we have for understanding the structure and evolution of the universe are measuring fluctuations in the cosmic microwave background (CMB) and observing the gravitational lensing of light arriving from distant sources. The former has already yielded a wealth of information about the geometry, expansion history, energy and matter content, and future evolution of the universe [1]. Similarly, lensing measurements have provided important information about the dark matter content of galaxies and clusters of galaxies, the cosmological distance scale, the physics of quasars, and extraterrestrial planets. Yet the observation of gravitational lensing is still considered to be in its infancy. Now, the Atacama Cosmology Telescope (ACT) Collaboration is publishing two papers in Physical Review Letters that combine both types of observations. Using data taken with the Atacama telescope in Chile, the first paper (Das et al.) reports on the first detection of gravitational lensing of CMB fluctuations determined entirely from microwave ( $148$ gigahertz) measurements [2]. In the second paper, Sherwin et al. make the concomitant inference that these fluctuations provide independent evidence for the presence of dark energy in the universe [3].

The fluctuations in the CMB (Fig. 1, top) originate primarily from the so-called epoch of last scattering, which occurred about $400, 000$ years after the big bang (at a redshift of $z \sim 1000$ ) when the temperature cooled sufficiently for electrons and nuclei to form atoms that were mostly transparent to the background of photons. The mass concentrations that act as gravitational lenses lie roughly halfway between us and the source of the CMB (at redshifts of $z \sim 2$ ). Their characteristic sizes are $\sim 300$ megaparsecs, which is the scale of the peak of the matter spatial power spectrum of the universe. The resulting gravitational potential wells deflect the photons in the microwave background by, on average, only $3$ arc minutes, so it is expected that the CMB angular power spectrum is only affected at these small angles. In fact, lensing does smear the power spectrum at this scale and leads to a suppression of small-scale features inherent in CMB fluctuations. (Static gravitational lenses cannot generate CMB fluctuations but only modify any fluctuations that are already present.) However, the characteristic lensing potential has an angular size of $\sim 2$ degrees. As a result, the deflection angles are also correlated on an angular scale of $\sim 2$ degrees.

In principle, measuring the distortions in the CMB caused by lensing would offer a way to infer the distribution of matter in the universe. The problem is that both the fluctuations in the CMB and the dispersal of matter are random distributions and untangling the two is, to say the least, challenging. Intrinsic CMB fluctuations have a very nearly Gaussian spectrum while the lensing potentials are determined by the large-scale mass distribution, which is also nearly Gaussian. The lensing of the microwave background, on the other hand, is proportional to the product of these two distributions and is therefore, distinctly non-Gaussian. Because small-scale CMB fluctuations are physically uncorrelated with the relatively nearby lensing masses, the small-scale three-point correlation function vanishes identically (or at least is very small). The four-point function is the lowest higher-order CMB correlation function that has a significant non-Gaussian component and it is this distinctive non-Gaussian characteristic that allowed the ACT team to detect the lensed component of CMB fluctuations in their data.

The most prominent features of the CMB angular power spectrum—essentially a spherical harmonic transform of the CMB—are the acoustic peaks (Fig. 1, bottom). These were generated by oscillations in the photon-baryon plasma shortly before the epoch of recombination—the time after which free electrons combined with protons and helium nuclei to form neutral atoms and the photons in the microwave background became uncoupled from matter. The peaks indicate an excess of fluctuations in the CMB at these particular scales. (Recent observations of both the South Pole Telescope [4] and ACT [5] have enabled acoustic peaks in the CMB power spectrum to be detected out to spherical harmonic order $l \sim 3000$ corresponding to angular scales of $\sim 0.06$ degrees.) The effect of gravitational lensing on the power spectrum is to broaden and attenuate the acoustic peaks at angular scales less than $0.2$ degrees ( $l > 1000$ ). In fact, there is evidence for this, though at a certainty below the $3 σ$ level [6]. A more definitive detection of CMB lensing was accomplished by correlating small-scale structure in the CMB with tracers of the lensing masses, such as radio galaxies and luminous red galaxies [7,8]. However, the most significant detection yet was accomplished by exploiting the non-Gaussian property of the lensing-induced $4$ -point correlation function as mentioned above. Even this technique required carefully isolating the non-Gaussian lensing signal from the Gaussian component in the $4$ -point function that is an order of magnitude larger. The detection was only significant at the $4 σ$ level; however, it was sufficient for Sherwin et al. to deduce the presence of dark energy, at a $3.2 σ$ level, entirely from measurements of the CMB.

The current lensing measurements are not particularly useful as a high-precision determination of the properties of the large-scale universe. Direct observations—such as the supernovae distance-redshift relation [9] and the presence of CMB fluctuations generated by collapsing, large-scale concentrations of dark matter (the integrated Sachs-Wolfe effect) [10]—and indirect observations, including the detailed structure of the CMB power spectrum [1], have provided stronger evidence for the existence of dark energy. Perhaps the primary significance of the present results is being the first of what promises to be many more accurate lensing CMB measurements. Similar results from the South Pole Telescope are imminent and the Planck Satellite Mission [11] will undoubtedly yield more accurate measurements of CMB lensing. The latter is one of many telescopes that, in the next decade, will likely detect the lensing of the polarization spectrum of the CMB. There is considerably more information in lensed polarization and, in addition, lensing has a larger effect on the polarization spectrum, which itself is relatively clean of foreground contamination. Finally, there are many other types of CMB observations that will help us understand the cosmos. These include the electric and magnetic field mode polarizations of the CMB, the integrated Sachs-Wolfe effect, and fluctuations in the CMB caused by the inverse Compton scattering of photons from hot, ionized gas in clusters of Galaxies (the thermal and kinetic Sunyaev-Zel’dovich effects).

Neither is the Sherwin et al. inference about the dark energy content of the universe by any means the only goal of such measurements. Future CMB observations will allow cosmologists to determine most of the cosmological parameters with unprecedented accuracy and inform us about how mass—both baryonic and dark matter—is distributed in the universe. Such measurements will also provide significant constraints on neutrino mass, the number of relativistic particles present at the epoch of recombination, the primordial helium abundance, and the injection of additional ionizing photons by dark matter self-annihilation. They may even significantly constrain the fundamental constants of physics [12].

Finally, I can’t resist commenting on the current characterization of cosmology as “big science.” The serendipitous discovery of the cosmic microwave background by Arno Penzias and Robert Wilson happened $46$ years ago. Two young junior faculty at Princeton, Peter Roll and Dave Wilkinson, had already constructed a small microwave radiometer to look for the CMB and, indeed, detected it a few months later. Many more relatively small-scale experiments were constructed in the next $25$ years to look for predicted fluctuations in the CMB and to confirm its black body spectrum. In 1990, the COBE satellite mission spectacularly confirmed the latter and two years later detected, for the first time, the small intrinsic fluctuations in the CMB. The last two decades have seen many more instruments of increasing complexity until today when the investigation of the CMB should truly be classified as big science. The number of authors on the papers featured in this commentary number no less than $41$ each, while the number of authors on the referenced South Pole Telescope and Planck papers are $44$ and $272$ , respectively. No longer can two or three scientists design and build an instrument, and then collect, analyze, and interpret the data. The expertise required in instrument design and fabrication, data collection, numerical analysis, and interpretation is enormous and necessarily involves a great many scientists and engineers with expertise in many different areas. Though this evolution is perhaps to be expected, one can remember fondly a time when cosmology was still a table-top endeavor.

References

E. Komatsu et al., Astrophys. J. Suppl. Ser. 192, 18 (2011)
S. Das et al., Phys. Rev. Lett. 107, 021301 (2011)
B. D. Sherwin et al., Phys. Rev. Lett. 107, 021302 (2011)
M. Lueker et al., Astrophys. J. 719, 1045 (2010)
R. Hlozek et al., arXiv:1105.4887 (2011)
M. Brown et al., Astrophys. J. 705, 978 (2009)
K. Smith, O. Zahn, and O Doré, Phys. Rev. D 76, 043510 (2007)
C. Hirata et al., Phys. Rev. D 78, 043520 (2008)
A. Conley et al., Astrophys. J. Suppl. Ser. 192, 1 (2011)
T. Giannantonio et al., Phys. Rev. D 77, 123520 (2008)
P. Ade et al. (Planck Collaboration), arXiv:1101.2022 (2011)
S. Galli et al., Phys. Rev. D 82, 123504 (2010)

About the Author

Stephen Boughn is John Farnum Professor of Astronomy at Haverford College and is currently Visiting Professor of Physics at Princeton University. He has interests in gravitation, cosmology, extragalactic astronomy, and the foundations of physics. His first foray into the CMB was an attempt to measure CMB fluctuations in 1968 when he was an undergraduate.