A new neutrino oscillation

Stephen J. Parke

Viewpoint

A new neutrino oscillation

Stephen J. Parke

Theoretical Physics Department, Fermi National Accelerator Laboratory, P.O. Box 500, Batavia, IL 60510, USA

July 18, 2011• Physics 4, 57

The T2K collaboration in Japan sees strong hints of muon neutrino to electron neutrino oscillation.

Figure caption — **Figure 1:** The flavor content of the neutrino mass eigenstates. The splitting between $ν_{3}$ and $ν_{2}$ (or $ν_{1}$ ) (labelled here by 1, 2, and 3) is responsible for oscillation at $500 km/GeV$ (relevant to neutrinos arriving from the Earth’s atmosphere), whereas the splitting between $ν_{2}$ and $ν_{1}$ leads to an oscillation at the scale of $15, 000 km/GeV$ (relevant to neutrinos arriving from the sun). $ν_{e}$ appearance at the T2K experiment is primarily controlled by the size of $\sin^{2} θ_{13}$ , the fraction of $ν_{e}$ in the $ν_{3}$ mass eigenstate.

Starting in the late 1960s, neutrino detectors began to see signs that neutrinos, now known to come in the flavors electron ( $ν_{e}$ ), muon ( $ν_{μ}$ ), and tau ( $ν_{τ}$ ), could transform from one flavor to another. The findings implied that neutrinos must have mass, since massless particles travel at the speed of light and their clocks, so to speak, don’t tick, thus they cannot change.

What has since been discovered is that neutrinos oscillate at two distinct scales, $500 km/GeV$ and $15, 000 km/GeV$ , which are defined by the baseline ( $L$ ) of the experiment (the distance the neutrino travels) divided by the neutrino energy ( $E$ ). Neutrinos of one flavor can oscillate into neutrinos of another flavor at both $L / E$ scales, but the amplitude of these oscillations is different for the two scales and depends on the initial and final flavor of the neutrinos. The neutrino states that propagate unchanged in time, the mass eigenstates $ν_{1}$ , $ν_{2}$ , $ν_{3}$ , are quantum mechanical mixtures of the electron, muon, and tau neutrino flavors, and the fraction of each flavor in a given mass eigenstate is controlled by three mixing angles and a complex phase. Two of these mixing angles are known with reasonable precision. An upper bound exists for the third angle, called $θ_{13}$ , which controls the size of the muon neutrino to electron neutrino oscillation at an $L / E$ of $500 km/GeV$ . The phase is completely unknown. The existence of this phase has important implications for the asymmetry between matter and antimatter we observe in the universe today.

Experiments around the world have steadily assembled this picture of neutrino oscillation, but evidence of muon neutrino to electron neutrino oscillation at $500 km/GeV$ has remained elusive. Now, a paper from the T2K (Tokai to Kamioka) experiment in Japan [1], reports the first possible observation of muon neutrinos oscillating into electron neutrinos at $500 km/GeV$ . They see $6$ candidate signal events, above an expected background of $1.5$ events. The probability that the $6$ events are all background is only about $0.7 %$ . Stated differently, this is a $2.7 σ$ indication that the parameter that controls the oscillation, the neutrino mixing angle $θ_{13}$ , is nonzero, just shy of the $3 σ$ requirement to claim “evidence for.” Nevertheless, this experiment provides the strongest indication to date that this oscillation actually occurs in nature.

To measure $θ_{13}$ , the T2K aimed a beam of muon neutrinos (produced by the JPARC accelerator complex in Tokai, Japan) to the $50 kT$ Super-Kamiokande experiment, a large underground detector $295$ kilometers away, and looked for a signal indicating the appearance of electron neutrinos. Unfortunately, the March $11$ , $2011$ earthquake damaged T2K’s accelerator and the collaboration is not expected to resume taking data until next year. Once it resumes, the collaboration is scheduled to take $50$ times more data, and should be in a good place to either definitively confirm, or set a stringent limit on, the neutrino oscillation. At the same time, results from the MINOS experiment already support the T2K findings. At a seminar at Fermilab on June $24$ , $2011$ , MINOS reported a $1.7 σ$ excess of electron neutrino appearance events over background [2].

Numerous other experiments are pursuing evidence of a nonzero $θ_{13}$ . Double Chooz in France, Daya Bay in China, and RENO in South Korea—which, unlike T2K, produce neutrinos in a nuclear reactor—are all looking for the disappearance of electron antineutrinos at an $L / E \approx 500 km/GeV$ . These experiments have either recently started or will soon start taking data, with Double Chooz likely to report their first results by the end of $2011$ or the early part of $2012$ . In addition, the NO $ν$ A experiment in the US will start data taking in $2013$ with a baseline of $810 km$ . Since it operates at a higher energy, NO $ν$ A will have the capability to study oscillations of both neutrinos and antineutrinos. The fact that the T2K experiments indicate not only a nonzero but a potentially large value of $θ_{13}$ is exciting news for all of these experiments, as there is now a good chance they will be able to measure the value of this mixing angle with some precision, as opposed to just setting a limit on it. This is particularly the case for the long baseline experiments, T2K and especially NO $ν$ A, which are looking for possible asymmetries between neutrinos and antineutrinos. Such asymmetries would tell us more about the ordering of the neutrino mass eigenstates. They may also reveal that neutrino physics violates charge-parity (CP) symmetry.

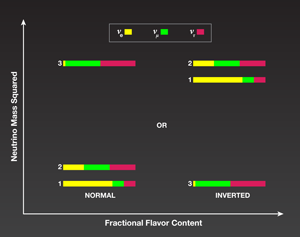
Figure 1 summarizes what is currently known about the flavor content of the three known neutrino mass eigenstates. (A more extensive review can be found in Ref. [3].) $ν_{1}$ has the highest electron neutrino component and $ν_{3}$ has the smallest electron neutrino component. Previous experiments have made measurements that determine the following: the muon neutrino component of $ν_{3}$ , which is controlled by the size of ${sin}^{2} θ_{23} \approx 1 / 2$ ; the electron neutrino component of $ν_{2}$ , which is controlled by the size of ${sin}^{2} θ_{12} \approx 1 / 3$ ; and the electron neutrino component of $ν_{3}$ , which is controlled by the size of ${sin}^{2} θ_{13}$ , which has been constrained to be less than $0.03$ from past experiments. The T2K results, which are a direct measure of the electron neutrino component of $ν_{3}$ , indicate that ${sin}^{2} θ_{13}$ is close to this bound of $3 %$ .

The size of the splitting (in mass squared) between $ν_{2}$ and $ν_{1}$ is $30$ times smaller than the splitting between $ν_{3}$ and $ν_{2}$ (or $ν_{1}$ ) ( $δ m_{21}^{2} \equiv m_{2}^{2} - m_{1}^{2} = + 7.6 \times 10^{- 5} {eV}^{2}$ compared to $| δ m_{32}^{2} | = 2.4 \times 10^{- 3} {eV}^{2}$ .) Also, it is known that $ν_{2}$ is heavier than $ν_{1}$ , but the relationship between the mass of $ν_{3}$ and $ν_{2}$ has yet to be determined. This ambiguity is reflected in Fig. 1. If the mass of $ν_{3}$ is greater than the mass of $ν_{2}$ and $ν_{1}$ , it is called a normal hierarchy; otherwise it is called an inverted hierarchy. There is one other unknown parameter in the neutrino mixing matrix with an effect on neutrino oscillations. It is a complex phase, which has a range between $0$ and $2 π$ . If $θ_{13}$ is large, as T2K hints it is, then the NO $ν$ A experiment has the possibility of determining the neutrino mass hierarchy for a sizeable fraction of the range of this complex phase.

This complex phase is interesting for another reason. It has an opposite sign for neutrinos and antineutrinos and appears in the interference between the oscillation amplitudes of the two $L / E$ scales, thus allowing for the possibility of CP violation for neutrinos. That is, the probability (in vacuum) of a muon neutrino oscillating into an electron neutrino is different than the probability that an antimuon neutrino will oscillate into an antielectron neutrino.

The possibility that $θ_{13}$ is large opens the very real possibility that CP violation can be observed in the next generation of neutrino experiments. One is the proposed Long Baseline Neutrino Experiment (LBNE), a large detector located at the Homestake mine in South Dakota in the path of an intense beam of neutrinos from Fermilab, $1300 km$ away. Observing CP violation in neutrino oscillations would provide support for the Leptogenesis hypothesis [4], which holds that the observed matter-antimatter asymmetry in the universe arises from an asymmetry in leptons. Finding a connection between neutrinos and the matter-antimatter asymmetry of the universe would be of monumental significance.

References

K. Abe et al. (T2K Collaboration), Phys. Rev. Lett. 107, 041801 (2011)
MINOS webpage: http://www-numi.fnal.gov/; MINOS seminar: http://theory.fnal.gov/jetp/talks/MINOSNue\_2011June24.pdf; P. Adamson et al. (The MINOS Collaboration), Phys. Rev. D 82, 051102 (2010)
H. Nunokawa, S. J. Parke, and J. W. F. Valle, Prog. Part. Nucl. Phys. 60, 338 (2008)
S. Davidson, E. Nardi, and Y. Nir, Phys. Rept. 466, 105 (2008)
O. Mena and S. J. Parke, Phys. Rev. D 69, 117301 (2004)

About the Author

Stephen Parke is the Head of the Theoretical Physics Department at the Fermi National Accelerator Laboratory. Besides neutrinos his research interests include top quarks, QCD, and magnetic monopoles.