Light doubles back

David L. Andrews

Viewpoint

Light doubles back

David L. Andrews

School of Chemistry, University of East Anglia, Norwich NR4 7TJ, United Kingdom

August 1, 2011• Physics 4, 60

Metamaterials can act as nonlinear mirrors, reflecting back an incoming electromagnetic wave at twice the frequency.

Figure caption — **Figure 1:** Coherence lengths for second harmonic radiation generated in the forward and backward directions, relative to the pump radiation of half the frequency, in the key frequency region around $1250 MHz$ . Over a limited range of frequencies below $1350 MHz$ , the retro-propagating harmonic is sustained over a greater distance than the conventional transmitted harmonic. The crossover of the “forward” and “backward” emission curves at $1350 MHz$ signifies a frequency at which the longitudinal component of the pump wave vector becomes zero, allowing harmonic emission to occur equally in either direction, under the same poling conditions.

It is half a century since Franken and co-workers first reported their landmark observations of optical second harmonic generation (SHG), using the recently developed ruby laser [1]. The principle of frequency doubling became fully comprehensible with subsequent theoretical analysis [2]; the rapidly ensuing, parallel development of experiment and theory essentially marked the birth of the diverse field we now call nonlinear optics. In SHG the pairwise annihilation of photons from an input beam provides for the creation of individual photons with twice the energy: commonly, each output photon has not only double the optical frequency but also double the photon momentum. Laserlike output is produced when the harmonic light develops in phase with the input, and in a real, dispersive material, one generally has to circumvent a potential phase mismatch by the use of birefringent or alternately layered materials. The pump laser input then provides for the forward emission of a coherent and strongly directed harmonic output; laser frequency conversion is the foremost among numerous widespread applications.

Following the earliest studies, it was recognized that coherent frequency doubling can also occur in a surface reflection geometry, where the harmonic emerges with conservation of the optical momentum component parallel to the surface. New work on SHG in a phase-matched metamaterial, conducted by Alec Rose, Da Huang, and David Smith at Duke University, North Carolina, and now reported in Physical Review Letters [3], represents a fresh, and highly significant departure from these long-established principles. In the rapidly growing field of metamaterials it is known that suitably constructed materials may display negative refraction, creating the conditions for a sustained momentum flux that points in the opposite direction to the optical propagation, and so giving rise to a range of exotic transmission and reflection features [4,5]. But it has also been shown that such systems hold extremely interesting potentialities for SHG. In suitable metamaterials, the principle of linear momentum conservation by the radiation field—crucial for securing a strong, coherent output—can in fact be satisfied in a mechanism that delivers harmonic radiation backwards, against the fundamental frequency input. Verifying earlier predictions by Agranovich et al. [6], this remarkable behavior has now been achieved experimentally.

The key to achieving some beautiful results has been the ability of the Duke University team to engineer a waveguide that will exhibit strikingly different dielectric and magnetic permeability properties, at appropriate fundamental and harmonic frequencies, so as to elicit negative refraction for the optical harmonic. Designed on general principles developed by Pendry et al. [7] and Zharov et al. [8], this is a system based on an aluminum waveguide, longitudinally loaded with magnetic nonlinear metamaterial components. Each unit cell comprises a split-ring resonator; the whole assembly can be deployed in periodically poled (static field-oriented) or unpoled configurations, allowing precise control over the phase-matching conditions by the judicious orientation of appropriate sections. Over a tightly confined range of microwave frequencies around $625$ megahertz, this waveguide thus not only provides for the propagation of an optical mode whose phase velocity opposes the direction of power flow, it can also generate conditions for the equally intriguing possibility of a wave vector that completely vanishes near the cutoff frequency.

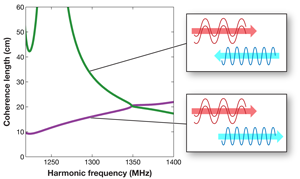
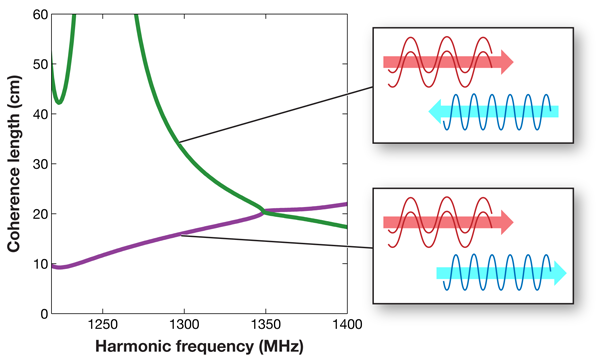
The characteristic coherence and directional properties of a fully phase-matched second harmonic signal are readily quantified in terms of coherence length, a measure of the distance over which the converted signal retains a constructive phase relationship with the pump. Periodic poling facilitates exact fulfillment of the phase matching, so that the coherence of the harmonic can be sustained over a useful distance. In support of their experimental observations, calculations by Rose et al. dramatically show that not only is there a range of frequencies over which “backwards” harmonic generation actually outweighs in intensity the forward harmonic emission, but also the coherence length for the retro-harmonic rises to meter-scale proportions, as shown in Fig. 1.

The promise of exotic nonlinear optical effects at relatively low power prompts questions of how one might achieve similar effects at much shorter wavelengths, closer to the visible range, although very different constructs will certainly be required [9]. Reflecting a general challenge for metamaterials, there is a significant obstacle to be overcome in securing the sought forms of magnetic permeability at these much higher optical frequencies. It is also interesting to entertain possible links with another rapidly developing area of optics, centering on vortex beams and orbital angular momentum. Here, it has long been known that such beams undergo second harmonic conversion with a retention of orbital angular momentum—in other words the forward-emitted harmonic photons not only have double the energy and linear momentum of the input—they also have twice the orbital angular momentum [10]. It will be fascinating to see if, as one might surmise, a similar principle might be verified for backward harmonic emission in metamaterials, suggesting a change of helicity as well as direction.

Much of the ongoing research in metamaterials has the ultimate aim of controlling and manipulating light, determining and developing a range of mechanisms that can be built into the next generation of photonic devices. With this new extension into optical nonlinearity, the new work by Rose et al. will undoubtedly pave the way for a host of studies pursuing further extensions of principle and application.

References

P. A. Franken, A. E. Hill, C. W. Peters, and G. Weinreich, Phys. Rev. Lett. 7, 118 (1961)
J. A. Armstrong, N. Bloembergen, J. Ducuing, and P. S. Pershan, Phys. Rev. 127, 1918 (1962)
A. Rose, D. Huang, and D. R. Smith, Phys. Rev. Lett. 107, 063902 (2011)
V. M. Shalaev, Nature Photon. 1, 41 (2006)
M. W. McCall and G. Dewar in Tutorials in Complex Photonic Media, edited by M. A. Noginov, G. Dewar, M. W. McCall, and N. I. Zheludev (SPIE, Bellingham 2009), pp. 1-31[Amazon][WorldCat]
V. M. Agranovich, Y. R. Shen, R. H. Baughman, and A. A.Zakhidov, Phys. Rev. B 69, 165112 (2004)
J. B. Pendry, A. J. Holden, D. J. Robbins, and W. J. Stewart, IEEE Trans. Microwave Theory Tech. 47, 2075 (1999)
A. A. Zharov, I. V. Shadrivov, and Y. S. Kivshar, Phys. Rev. Lett. 91, 037401 (2003)
C. M. Soukoulis, S. Linden, and M. Wegener, Science 315, 47 (2007)
K. Dholakia, N. B. Simpson, M. J. Padgett, and L. Allen, Phys. Rev. A 54, R3742 (1996)

About the Author

David Andrews is Professor of Chemical Physics at the University of East Anglia, where his group conducts research on fundamental photonics, optomechanical forces, nonlinear optics, energy harvesting and molecular energy transport. He has over $250$ research papers and a dozen books to his name. He is a Fellow of the Institute of Physics, the Royal Society of Chemistry, and the SPIE.