Rush hour in a drop of coffee
A drop of fluid dries, a pattern forms. Could anything be more mundane? Yet, as technological designs call for ever smaller devices, understanding how the flow of a particle-laden fluid could control the deposition of tiny objects is actually becoming a compelling intellectual challenge. In many applications, ranging from aggregating proteins to high-density information storage and photonics, the physics of how evaporating fluid can shape a pattern—the so-called coffee ring stain—looms large. Now, writing in Physical Review Letters, Álvaro Marín and colleagues at the University of Twente in the Netherlands report experiments in which they have tracked the structural pattern and dynamics of particles at the edge of the canonical ringlike stain [1].
Research on the coffee-ring phenomenon began with Sidney Nagel, a physics professor at the University of Chicago, who was curious about the form of coffee stains on his kitchen countertops [2]. Nagel’s befuddlement, which he shared with his colleagues, could be stated this way: Why does all the material suspended in a drop of coffee end up at the edge when the drop evaporates, considering that it started out dispersed across the whole drop? The effect was common to all droplets of dispersed colloidal objects, including milk, blood, ink, and paint, evaporating on a wide variety of surfaces, suggesting there should be a general explanation.
The physical picture that emerged was beautiful and simple: As the droplet dries, the liquid evaporating from the thinning outer edge, where the contact angle θ is shrinking to zero, must be replenished by liquid from the drop’s interior. This sets up a strong outward flow in the solvent, which carries most of the solute to the contact line. Pre-existing surface roughness can provide the force to pin the contact line, but the contact line further pins itself through a feedback loop between flow and patterning: the outward flow increases the deposition of solute, which serves to anchor the fluid and reinforce the outward flow.
The simplicity of this picture carries some caveats—the suppression of counterflows that are due to gradients in surface tension (Marangoni flows) is one example. However, in the years since Nagel’s observation, the coffee ring has taken on a life of its own. Special-effects artists at the University of Washington and Pixar, for example, used the theory to improve their computer rendering of the luminous textures of watercolor paintings [3].
While the basic principles of the ringlike stain were first understood 15 years ago, a complete picture of how the deposition evolves in space and time have remained elusive. This is partly because we now appreciate how complicated the coffee-ring effect actually is: the contact-line dynamics are subtle (such as depinning-repinning cycles) and researchers are discovering an expanding taxonomy of patterns (such as multiple rings, stripes, spikes, chevrons, and fractal-like lace) [4–6]. But even for the classic coffee ring, detailed microscopic information connecting structure to dynamics has simply not been available.
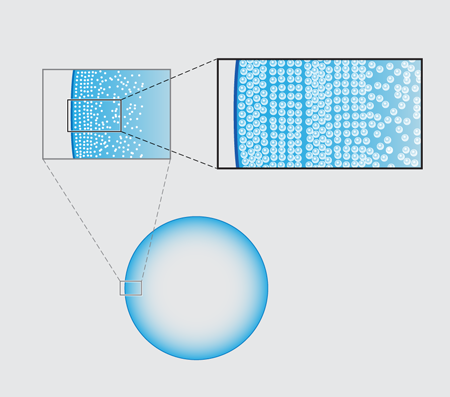
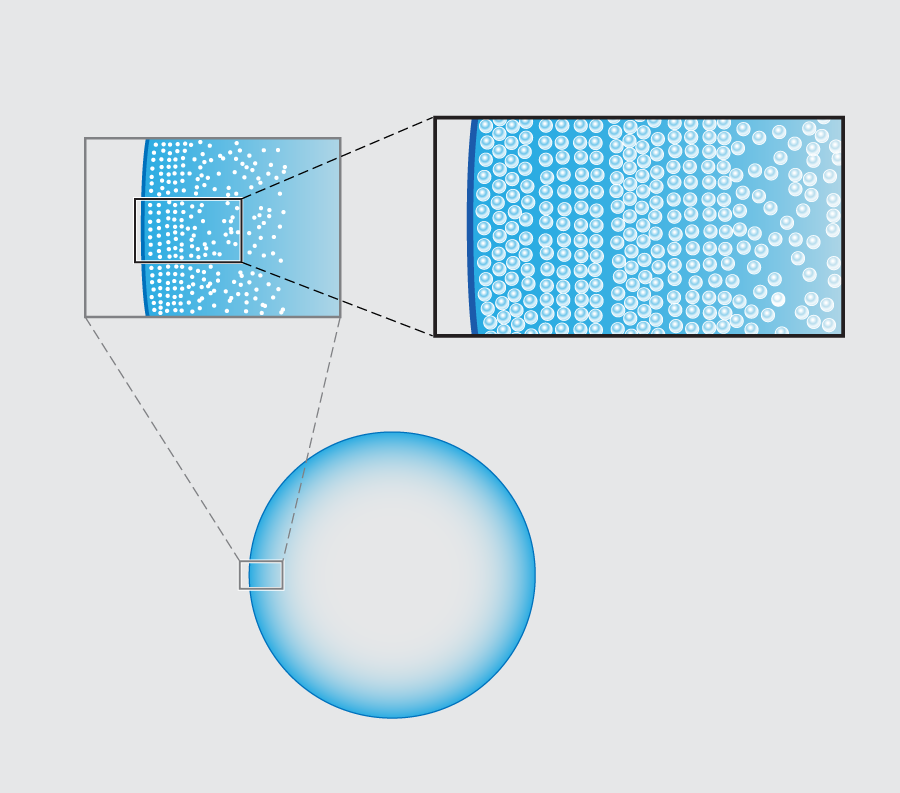
In their new experiments, Marín et al. follow the entire time evolution of a 3-microliter water droplet laden with micron-diameter fluorescent polystyrene beads sitting on a glass slide. Viewing the underside of the drop using an inverted microscope, they observe that there is a clear spatial dependence in the structure of the resulting ring as one moves in from the contact line toward the center of the droplet. Most dramatically, they see a structural transition from beads that are ordered, as in a crystal, to a more disordered packing arrangement (Fig. 1 ).
In order to pin down the origin of the patterning, the group tracked the particle velocities using micro-particle image velocimetry ( μPIV). Their basic result is quite simple: the spatial transition from ordered, crystalline arrays to disordered packings stems from a dramatic temporal speed up of the particle motion near the end of the evaporation, which the Twente team refer to as “the rush hour effect”. The observation of this effect is not in itself new. A consequence of mass balance is that the height-averaged radial velocity u at a distance x from the droplet’s edge behaves like u∼1/(θ√x). This implies both a spatial and temporal divergence of the particle velocity (as x and θ approach zero, respectively) in the last stage of the droplet’s life [2]. Marín et al.’s novel point is to argue that the particles forming the ordered phase arrive early at the contact line, when the deposition rate is low; those forming the disordered phase arrive during rush hour, at high deposition rates. The slow-to-arrive particles have the time to position themselves by diffusion into a snug arrangement, but those coming at rush hour have no time to find an optimal fit and are quenched into a jammed packing.
This Brownian version of particle ordering (which the authors liken to a game of Tetris) can be expressed as a comparison of time scales: on the one hand, the Einstein-relation timescale τ=d2/D, where d is the particle diameter, and D the particle diffusivity; on the other hand, the hydrodynamic timescale t=L/u, where L is the average distance between nearby particles (a function of particle concentration). The critical velocity when these two timescales coincide is then u∼LD/d2. Marín et al.’s μPIV measurements of the velocity one particle diameter above the substrate for various particle sizes and concentrations enable them to experimentally determine the critical time and velocity for the onset of the order-disorder transition. Indeed, they find that their experimental velocities closely match those given by the comparison of hydrodynamic and diffusive rates.
Direct confirmation of the three-dimensional structure of the various colloidal packings is still missing. Marín et al. present both light microscopy of the bottom layer and scanning electron micrograph (SEM) images. These show ordered phases that appear square and hexagonal (Fig. 1, top right). Both are, plausibly, hexagonal close-packed (hcp) lattices, since different planar patterns can appear depending on the orientation of the crystal symmetry axes with respect to the plane of the substrate. What controls these orientational transitions is the effect of the confinement of a small number of layers between the substrate and the liquid-vapor interface. In two dimensions, hexagonal packing is the most efficient way to pack spheres, and in an unconstrained, three-dimensional space, hcp is the most favorable. But in a confined wedge space, whenever a new layer of particles is deposited, the square packing is slightly denser. A similar situation occurs when colloids are confined between planar walls, or in a cylindrical capillary [7,8]. Close examination of the SEM images of Marín et al. suggests that the hexagon-to-square transition occurs where a new layer appears, whereas the square-to-hexagon transition appears within a single layer.
The idea that kinetics prevents a system from being able to fully explore configuration space is well known for the glass transition, where fast temperature quenches and applied stresses have been studied for decades. By comparison, the analogous idea for colloidal systems is relatively new. A sure lesson of the present work is this: the dynamics of the deposition, rather than the stability of static packing arrangements, determines the patterns that ultimately form [9–11].
Perhaps the final missing piece of the coffee-ring puzzle is a “4D” picture of the deposition at the edge. How does this jittery game of microscopic Tetris actually play out in three dimensions plus time? Is there a fluid layer remaining above the deposit? If so, what is the nature of this layer and does it alter the evaporative and fluid fluxes at the edge? As for the problems that remain, like the coffee stains on Nagel’s countertop, it’s fair to say that so far no one has them completely licked.
References
- Á. G. Marín, H. Gelderblom, D. Lohse, and J. H. Snoeijer, Phys. Rev. Lett. 107, 085502 (2011)
- R. D. Deegan et al., Nature 389, 827 (1997); Phys. Rev. E 62, 756 (2000)
- C. J. Curtis et al., in Proceedings of SIGGRAPH '97, (ACM Press/Addison-Wesley, New York, 1997)[Amazon][WorldCat]; Cassidy Curtis and Kurt Fleischer (private communication)
- A.-M. Cazabat and G. Guena, Soft Matter 6, 2591 (2010)
- R. D. Deegan, Phys. Rev. E 61, 475 (2000)
- C. Allain and L. Limat, Phys. Rev. Lett. 74, 2981 (1995); L. Pauchard, F. Parisse, and C. Allain, Phys. Rev. E 59, 3737 (1999)
- P. Pieranski, L. Strzelecki, and B. Pansu, Phys. Rev. Lett. 50, 900 (1983)
- M. Abkarian, J. Nunes, and H. A. Stone, J. Am. Chem. Soc. 126, 5987 (2004)
- I. Cohen, T. G. Mason, and D. A. Weitz, Phys. Rev. Lett. 93, 046001 (2004)
- G. R. Farrell, K. M. Martini, and N. Menon, Soft Matter 6, 2925 (2010)
- L. T. Shereda, R. G. Larson, and M. J. Solomon, Phys. Rev. Lett. 101, 038301 (2008)