Majorana fermions inch closer to reality
The search for Majorana fermions is quickly becoming an obsession in the condensed-matter community. To understand the intense interest, I will begin with a practical definition: a Majorana fermion is a fermion that is its own antiparticle. While sophisticated particle physics experiments are testing for Majorana character in neutrinos propagating in three dimensions [1], solid state physicists are more interested in lower dimensional counterparts. The most interesting Majorana fermions that are predicted to appear in materials are zero-dimensional bound states confined to live on various types of topological defects [2]. In a paper published in Physical Review Letters, Pavan Hosur and collaborators from the University of California, Berkeley, predict that these bound states are found in the vortices of the superconductor [3] (Fig. 1). Once discovered, a set of zero-dimensional Majorana bound states (MBS) are predicted to exhibit exotic non-Abelian statistics when exchanged among each other. While of great fundamental interest, perhaps the biggest driving factor in the search is a well-regarded proposal for (topological) quantum computation, which uses this unique statistical property of the MBS to robustly process quantum information free from local sources of decoherence [4,5].
With the high-energy and condensed-matter communities exerting so much effort to find Majorana fermions, it is a bit surprising they have not yet been discovered. Why are Majorana fermions naturally elusive, at least in a condensed-matter setting? To determine if an electron, for example, is its own antiparticle we can perform a simple test: shoot two identical electrons at each other and look at the outcome. If there is a finite probability that the electrons annihilate into the fermionic vacuum, then they could be Majorana fermions. However, we know, for example, that electric charge is conserved and thus the two electrons can never annihilate, and are thus not Majorana. Electrons, in fact, have an independent antiparticle, the positron, which has different quantum numbers (e.g., opposite electric charge).
Naively, this eliminates all fermions at play in conventional electronic systems from being Majorana. The key to getting around this obstacle is noting that one finds many different emergent fermionic vacua/ground states in electronic systems that are qualitatively different from the fundamental vacuum of spacetime. To illustrate this, consider a BCS superconductor ground state filled with a condensate of paired electrons. If we again scatter two electrons off each other, they can indeed bind into a Cooper pair and “annihilate” into the fermionic vacuum! However, if the vacuum is of -wave character, the most common superconducting ground state, then the two electrons bound into the Cooper pair must have opposite spin and are thus not Majorana (the antiparticle of an electron with spin up, in this case, is one with spin down). The solution to this problem is manifest: we must find a way to get around the spin-quantum number. Currently, there are two primary mechanisms to do this: (i) the superconducting vacuum can have spin-triplet pairing, which pairs electrons with the same spin or (ii) the superconductivity can exist in the presence of spin-orbit coupling or some other mechanism which will remove the spin conservation. Solution (i) is the paradigm for the first proposals of the existence of MBS as quasiparticles of a fractional quantum Hall state which models a two-dimensional electron gas at filling [6], and as vortex excitations in some theories of the unconventional superconducting state of [7]. These proposals offer real material candidates for finding MBS, but experiments in both of these systems require utmost care in sample production and measurement precision. To date, MBS excitations have not been clearly distinguished in either of these systems. Recently, solution (ii), which was first implemented by Fu and Kane in topological insulator/superconductor heterostructures [8], has been garnering attention due to more inherent practicality. This has been followed up nicely with further predictions of MBS in low-dimensional spin-orbit-coupled heterostructures in proximity to -wave superconductors [9].
The seminal proposal of Fu and Kane predicts that if the surface of a three-dimensional topological insulator is proximity-coupled to an -wave superconductor, then vortex lines in the superconductor will trap MBS where the lines intersect the topological insulator surface [8]. This proposal requires two main ingredients: (i) a topological insulator and (ii) an -wave superconductor that can effectively proximity-couple to the surface of the topological insulator. Despite all of the recent publicity about the discovery of three-dimensional topological insulators [10], finding a suitable topological insulator for these experiments is still a difficult task. The reason being that, as of yet, there are no topological insulator materials that are completely insulating in the bulk, despite intense experimental programs dedicated to this task. The most commonly studied topological insulators are variations of either or , in which it has been difficult to tune the bulk to a completely insulating state [11]. Thus, while many experiments have confirmed the robust nature and structure of the surface states, these materials, having bulk carriers, are not true topological insulators.
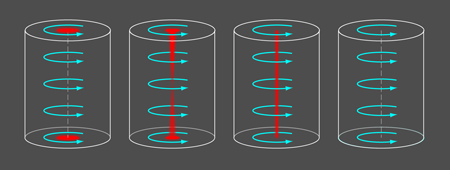
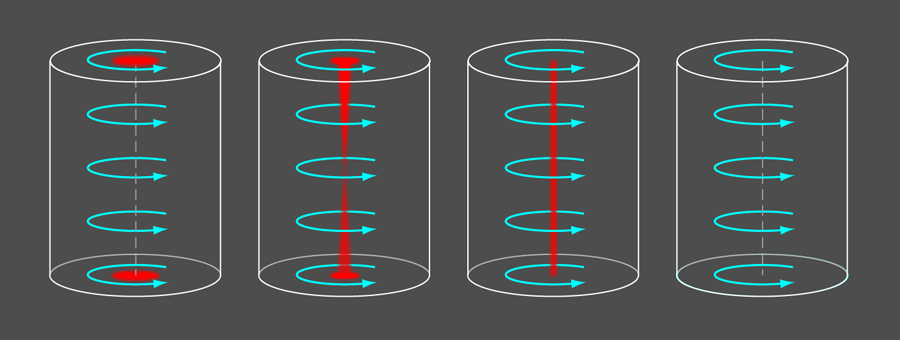
It is then natural to ask, What is a doped topological insulator good for? While one hopes that many of the topological phenomena of the true insulating state might be manifested in some form in a doped system, many questions still remain unanswered. However, Hosur et al. have made a striking prediction that MBS can still be realized in doped topological insulators under certain mild conditions [3]. A true insulating state is important in the Fu-Kane proposal because if the bulk contains low-energy states then the MBS can tunnel away from the surface and delocalize into the bulk, which effectively destroys the MBS. Hosur et al. circumvent this delocalization by requiring that the entire doped topological insulator become superconducting. They show that as long as the doping is not too large, vortices in superconducting topological insulators will bind MBS at the places where the vortex lines intersect the material surfaces. While this might seem like a big leap in complexity, experimental evidence already shows that, indeed, copper-doped is a superconductor below [12]. In this context, Hosur et al. make a strong prediction that vortex lines in superconducting can harbor MBS.
To understand the prediction, we begin with the Fu-Kane proximity effect scenario, as mentioned above, with a vortex line stretched between two surfaces. MBS are trapped where each end of the vortex line meets the topological insulator surface (see Fig. 1). If we tune the bulk chemical potential to lie in the conduction band, as opposed to the nominal insulating gap, then the MBS on each end of the vortex line could tunnel through the bulk and hybridize with the state on the opposite end. This is prevented in Hosur et al.’s work by inducing a superconducting gap in the entire bulk so that the MBS remain trapped. If the superconducting state were homogeneous, then the MBS would be trapped on the ends of the vortex line for any doping level. However, the superconducting order parameter varies rapidly near the vortex core, which is essentially a thin tube of normal metal (doped topological insulator) containing bound states with energies that lie below the nominal superconducting gap. It is easiest for the MBS to tunnel through the “mini-gap” region in the vortex core, and in fact, Hosur et al. go on to show that there is a critical chemical potential level where a vortex-core bound state becomes gapless and the MBS can easily tunnel through the vortex line to annihilate. Beyond this critical doping, the vortex line re-enters a gapped phase, but the MBS are absent. See Fig. 1 for an illustration of this process. The critical chemical potential can be calculated solely from low-energy information about the Fermi surface, and depends on the orientation of the vortex line with respect to the crystal structure. It is estimated that vortex lines oriented along the axis of are just on the trivial side of the transition, while vortices perpendicular to the axis should be well within the nontrivial regime and should trap MBS.
If is indeed in the predicted experimental regime, then this development is an exciting breakthrough, since it offers a simple way to generate MBS in a system that already exists. These effects show that, up to a certain point, a doped topological insulator remembers something about its topological nature, and furthermore that we are tantalizingly close to the first observation of MBS.
References
- F. T. Avignone, III, S. R. Elliott, and J. Engel, Rev. Mod. Phys. 80, 481 (2008)
- D. A. Ivanov, Phys. Rev. Lett. 86, 268 (2001)
- P. Hosur, P. Ghaemi, R. S. K. Mong, and A. Vishwanath, Phys. Rev. Lett. 107, 097001 (2011)
- A. Yu. Kitaev, Ann. Phys. (N.Y.) 303, 2 (2003)
- C. Nayak, S. H. Simon, A. Stern, M. Freedman, and S. Das Sarma, Rev. Mod. Phys. 80, 1083 (2008)
- G. Moore and N. Read, Nucl. Phys. B360, 362 (1991)
- N. Read and D. Green, Phys. Rev. B 61, 10267 (2000)
- L. Fu and C. L. Kane, Phys. Rev. Lett. 100, 096407 (2008)
- J. D. Sau, R. M. Lutchyn, S. Tewari, and S. Das Sarma, Phys. Rev. Lett. 104, 040502 (2010)
- X.-L. Qi and S.-C. Zhang, Phys. Today 63, No. 1, 33 (2010)
- M. Z. Hasan and C. L. Kane, Rev. Mod. Phys. 82, 3045 (2010)
- Y. S. Hor, A. J. Williams, J. G. Checkelsky, P. Roushan, J. Seo, Q. Xu, H. W. Zandbergen, A. Yazdani, N. P. Ong, and R. J. Cava, Phys. Rev. Lett. 104, 057001 (2010)