Airy plasmons defeat diffraction on the surface
Surface plasmons (SPs), or more exactly, surface plasmon polaritons, are surface electromagnetic waves that propagate along the planar interface between a metal and a dielectric material [1] (see Fig. 1). These particular electromagnetic modes are sustained by the collective electronic oscillations (plasma waves) in the metal in proximity to the interface. Plasmons are essentially two-dimensional waves whose field components decay exponentially with distance from the surface. The very fact that these waves tightly cling to the surface makes them ideal for molecule diagnostics and biosensing applications. On many occasions, SP beams are expected to carry energy from one location on the surface to another. Yet for this to happen in an effective way, diffraction broadening effects must be first suppressed.
Methods to suppress the diffraction broadening of a freely propagating plasmon beam have been actively pursued by several research groups in recent years. For many applications, this diffraction-free plasmonic energy transport would need to occur even if there were imperfections on the surface. In a recent paper in Physical Review Letters, Alexander Minovich at the Australian National University in Canberra and his colleagues report the experimental observation [2] of a new class of plasmon-polariton waves that could offer such a solution: the so-called Airy-plasmon waves [3]. In general, Airy plasmons can exhibit a host of appealing characteristics. Not only can they retain their intensity features up to several diffraction lengths, but they can also self-heal and accelerate (self-bend along a parabolic trajectory) during propagation. Apart from being interesting in their own right, Airy plasmons may also hold promise for new, exciting applications in the general area of plasmonics.
Diffraction is a ubiquitous process in nature. Under the action of this effect, any confined beam carrying finite power is known to expand during propagation. The familiar spread of a Gaussian optical beam is just another example of this process. Loosely speaking, one can understand this phenomenon by considering the walk-off effects taking place between all the plane waves comprising a wave packet. The possibility of either engineering or suppressing diffraction effects—at least up to a certain distance of interest—was first tackled by Durnin, Miceli, and Eberly in their classic paper on Bessel beams [4]. In this work, it was recognized that diffraction effects can be deliberately “delayed” by using Bessel wave fronts—perhaps the best known example of a “diffraction-free” field. What they also realized was that all possible two-dimensional diffraction-free waves result from a conical superposition of plane waves. This is so because all the plane wave components involved share the same propagation vector along the path of propagation, and hence the beam intensity profile resulting from this superposition remains invariant. Given that this conical addition can be arranged in a number of different ways, it is clear that, in principle, one could come up with infinitely many such diffraction-free-field arrangements—with the Bessel family being just one of them.
Diffractionless fields are normal propagation modes (very much like a plane wave) and as such, in principle, they are supposed to carry infinite power. In practice, however, because of finite aperture effects, even these “privileged” beams are eventually subjected to the effects of diffraction. Yet, if the size of the aperture is considerably bigger than any of the intensity features of this wave front, the beam will propagate virtually undistorted until diffraction associated with the aperture itself starts to take its toll. Thus, for all practical purposes, the diffraction process is slowed down over the intended distance of propagation, and for this reason these beams are called “diffraction-free.” Nowadays such diffractionless beams find interesting applications in many and diverse settings ranging from biosensing to nonlinear optics.
At this point it is perhaps natural for one to ask if similar concepts can be used in plasmonics. In other words, is it possible to achieve diffraction-free propagation using plasmon beams along the surface of a metal? If so, will the scheme of conical superposition also work in this case? Surprisingly, the answer to the latter question is no. The very fact that a surface plasmon polariton can only exist in flatland renders the diffraction process one-dimensional. In turn, this reduction in dimensionality does not allow meaningful diffraction-free patterns through conical superposition [2]. Yet one-dimensional (1D) diffraction-free waves do exist. This discovery was made more than thirty years ago by Berry and Balazs, who showed that the force-free quantum mechanical Schrödinger equation can admit a unique, nonspreading accelerating solution in the form of an Airy wave packet [5]. These Airy packets are in a class by themselves and do not result from any conical addition.
The realization that Airy waves can be actually observed in optics came only recently [6,7]. In fact, in this realm, the beam’s acceleration takes on a whole new meaning. It means that during propagation, the intensity features of an optical Airy beam can self-bend, even in free space, and this without violating the premises of Ehrenfest’s theorem, which governs the centroid trajectory. Interestingly, Airy beams can propagate along parabolic paths, very much like cannon balls moving under the force of gravity. Subsequent experimental studies also demonstrated that these beams tend to self-heal themselves after encountering any perturbations—a property shared by all diffraction-free beams.
Earlier last year, the prospect of observing nondiffracting Airy plasmon waves was theoretically suggested by our group [3]. As mentioned before, the Airy plasmon wave packet is unique since it represents the only possible one-dimensional diffraction-free solution. In this realization, an Airy plasmon can propagate almost undistorted over several diffraction lengths along the metal surface. This occurs while its intensity features parabolically self-bend as a function of distance. In general, the beam can maintain the size of its lobes—a valuable property, especially when resolution is needed. Even more importantly, because of its self-healing characteristics, the Airy plasmon happens to be resilient against surface perturbations. This is a desirable feature given that surface plasmon polaritons tend to lose or radiate energy because of surface imperfections.
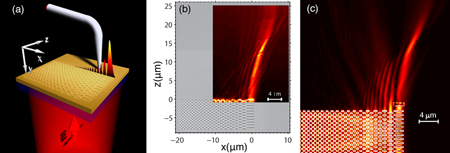
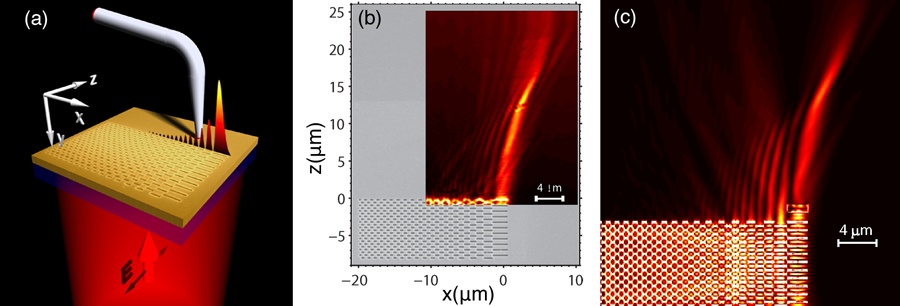
Minovich and colleagues report the experimental observation of such a surface Airy plasmon. Their experiments were carried out on an air-gold interface at a wavelength of nanometers (nm). In this arrangement a -nm-thick gold film was deposited on a glass substrate. A diffraction arrangement was fabricated by selectively removing the metal using focused ion-beam techniques, as shown in Fig. 1(a). This was used as a platform to couple a broader wave front of microns into a plasmon and shape the resulting beam into an Airy profile. This is achieved by manipulating both amplitude and phase of the optical field. The propagation dynamics of the Airy plasmon are then monitored using a near-field scanning optical microscope gold-coated fiber tip close to the surface. Experimental near-field results are shown in Fig. 1(b) and clearly demonstrate the anticipated effects. The main lobe of the Airy plasmon can maintain its width ( nm) up to several Rayleigh lengths while it also parabolically self-bends—a key characteristic of an Airy beam. In addition, self-healing is possible, as also depicted in Fig. 1(c).
This field is only now beginning. Interestingly, since the submission of this paper, Airy plasmons have also been reported by other groups. These studies were carried out independently at the University of California, Berkley, and Nanjing University, China [8,9]. These works are expected to stimulate more efforts towards a better understanding and utilization of nondiffracting Airy plasmons. As the authors of the accompanying paper indicate, surface Airy plasmons may open new opportunities for selective on-chip manipulation of nanoparticles and optical sensing circuitry. It will be of interest to see if, in the future, such ideas may spill over in other emerging disciplines of plasmonics.
References
- W. L. Barnes, A. Dereux, and T. W. Ebbesen, Nature 424, 824 (2003)
- A. Minovich, A. E. Klein, N. Janunts, T. Pertsch, D. N. Neshev, and Yu. S. Kivshar, Phys. Rev. Lett. 107, 116802 (2011)
- A. Salandrino and D. N. Christodoulides, Opt. Lett. 35, 2082 (2010)
- J. Durnin, J. J. Miceli, and J. H. Eberly, Phys. Rev. Lett. 58, 1499 (1987)
- M. V. Berry and N. L. Balazs, Am. J. Phys. 47, 264 (1979)
- G. A. Siviloglou and D. N. Christodoulides, Opt. Lett. 32, 979 (2007)
- G. A. Siviloglou, J. Brokly, A. Dogariu, and D. N. Christodoulides, Phys. Rev. Lett. 99, 213901 (2007); Opt. Express 16, 12880 (2008)
- P. Zhang, S. Wang, Y. Liu, X. Yin, C. Lu, Z. Chen, and X. Zhang, Opt. Lett. 36, 3191 (2011)
- L. Li, T. Li, S. M. Wang, and S. N. Zhu, Phys. Rev. Lett. (to be published); arXiv:1105.3160