Surface nanobubbles or Knudsen bubbles?

Vincent S. J. Craig

Viewpoint

Surface nanobubbles or Knudsen bubbles?

Department of Applied Mathematics, Research School of Physics and Engineering, Australian National University, Canberra ACT 0200, Australia

September 6, 2011• Physics 4, 70

AFM experiments suggest the long lifetime of surface nanobubbles is due to a balanced influx and outflux of gas molecules.

Figure caption — **Figure 1:** Schematic showing particles in a Knudsen gas leaving and entering a surface nanobubble with angle $θ$ to the surface.

The mysterious stability of nanobubbles on surfaces is a puzzle baffling soft matter and colloid scientists. Bubbles inside a fluid tend to be spherical, but surface bubbles have the appearance of blisters with typical widths of $1000$ nanometers (nm) and heights of $20 nm$ . The existence of surface bubbles was proposed to explain the extremely long range and the magnitude of the strongly attractive forces observed between hydrophobic surfaces in water [1]. Nanobubbles are of interest because they are easily produced and are stable, and as such, their presence may be altering many aqueous interfaces and exerting influence on processes as diverse as froth flotation to the transportation of anticancer drugs across membranes. Classically, bubbles will deflate, leading to an increase in Laplace pressure (the pressure differential inside and outside a bubble) and a positive feedback loop that results in their rapid disappearance. However, surface nanobubbles, seemingly unaware of the rules, can remain stable for days. Now, writing in Physical Review Letters, James Seddon and coauthors [2] at the University of Twente, the Netherlands, have proposed an explanation for this stability, whereby the properties of the gas within a nanobubble generate a recirculation of the surrounding liquid, which effectively ensures that the gas escaping the bubble through diffusion is recaptured and the bubble lifetime is extended.

The existence of surface nanobubbles was confirmed through atomic force microscope images, produced by groups in China [3] and Japan [4]. The Chinese group, led by Jun Hu, demonstrated that the creation of nanobubbles on a hydrophobic surface could be induced through a technique known as solvent exchange. Typically, the solvents employed are water and ethanol, which are miscible. When water displaces ethanol, a pure ethanol phase momentarily wets the surface before diffusing into the water. In doing so, excess gas is left behind at the interface and spherical cap nanobubbles are formed, with heights typically $< 100 nm$ and widths up to $10$ microns. For their part, the Japanese group of Ishida and Higashitani showed that the process of immersing a hydrophobic surface in water leads to incomplete wetting and the production of nanobubbles. Nanobubbles can also be produced by electrolysis and temperature change. As ethanol is often employed in cleaning regimes and the temperature changes required to induce nanobubbles are small ( $< 10$ ° $C$ ), it can be seen that nanobubbles may be present in a great many circumstances. Additionally, AFM studies reveal that the contact angle of nanobubbles is significantly higher (as measured through the more dense aqueous phase) than microscopic bubbles and that stability is largely unaffected by pH, electrolytes, and surfactants. The stability of nanobubbles has been a central question since they were first suggested. So what is the source of this surprising stability? We must consider two scenarios, both of which, at first glance, appear unlikely: either gas is not leaving the bubble, or it is leaving the bubble, but it is being replaced at approximately the same rate.

Even the purest of solutions contain quantities of insoluble material. William Ducker proposed that this insoluble material accumulates at the surface of nanobubbles, and in doing so, decreases the surface tension and thereby the Laplace pressure [5]. This would also alter the contact angle. From experiments, we now know that nanobubbles become unstable at high surfactant concentrations. The inference is that the stabilizing material is transported from the nanobubble surface to the surfactant micelles by the detergent action of the surfactant. An alternative explanation is that the oil-like interior of a micelle is a sink for gas molecules and the resulting increase in gas solubility leads to the disappearance of nanobubbles.

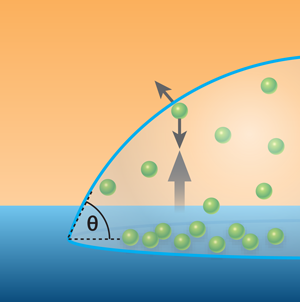
The Twente group has investigated the second scenario, that is, diffusion out of nanobubbles is occurring, but a dynamic equilibrium exists such that gas molecules return to the nanobubble and long term stability results [6]. The development of these ideas over several years has led to the current work. The most recent advance assumes that nanobubbles are so small that in most cases a gas molecule passing from one side to the other will do so without colliding with another gas molecule. Such a gas is called a Knudsen gas. The Twente group argues that gas molecules within the nanobubble have a net flow towards the gas-liquid interface (see Fig. 1) due to the difference between the surface facing out and that facing the fluid, and that the collisions that would normally randomize such a flow do not take place in a Knudsen gas. As molecules dissolve into the liquid, the momentum transfer leads to a circulating flow in the liquid near the interface that returns the gas molecules to the substrate, and ultimately, the nanobubble. The energy required to drive this flow is small and can be supplied thermally by the substrate over the timescale that nanobubbles are observed. The team also provides force measurements taken above a nanobubble as evidence of this flow. Of course, this theory is predicated on the gas being a Knudsen gas. When bubbles exceed a certain height (calculated to be $\sim 100 nm$ ), the Knudsen conditions are no longer met and the mechanism ceases to operate. Hence acceptance of this theory would rightly lead to nanobubbles at surfaces becoming known as “Knudsen bubbles.”

Complicating the case for this mechanism are reports that nanobubbles are also stable in bulk solution. The group of To Ngai in Hong Kong uses nanobubbles to induce a depletion force that is measured by total internal reflection microscopy [7], and recently, Ohgaki and co-workers in Osaka have shown images of bulk nanobubble replicas obtained using freeze fracture, and they report that nanobubble lifetime extends to two weeks [8]. Such bubbles cannot be stabilised by the Knudsen bubble model, which is dependent on the symmetry-breaking effect of the surface. However, the alternative explanation of Ducker [5] can still be applied to bulk nanobubbles. Hence, for these and other reasons, the nanobubble community is eagerly anticipating independent verification of bulk nanobubbles.

Another challenge to the Twente model is the observation of a gas phase at surfaces with an altogether different morphology. Known as “micropancakes” because of their shape [9], these gas phases extend large distances laterally but are only a few nanometers high. Their upper surface is parallel with the substrate. Furthermore, they can coexist with nanobubbles, and nanobubbles are even observed on top of micropancakes. The recognition that nanobubbles and other gaseous objects are stable challenges our understanding and requires that we consider the role they may be playing in many processes. This work defines an upper bound for the height of nanobubbles and connects the surprisingly high contact angles between the bubble and the surface, exhibited by nanobubbles, to their stability. The Twente group theorizes that the bubble is filled with a so-called Knudsen gas, which is so dilute that the mean free path is larger than the containing vessel, or in this case, bubble. As such, the very small size of surface nanobubbles—or Knudsen bubbles—may be the source of their stability rather than the cause of their disappearance.

References

J. L. Parker, P. M. Claesson, and P. Attard, J. Phys. Chem. 98, 8468 (1994)
J. R. T. Seddon, H. J. W. Zandvliet, and D. Lohse, Phys. Rev. Lett. 107, 116101 (2011)
S. T. Lou Z. Q. Ouyang, Y. Zhang, X. J. Li, J. Hu, M. Q. Li, and F. J. Yang, J. Vac. Sci. Technol. B 18, 2573 (2000)
N. Ishida, T. Inoue, M. Miyahara, and K. Higashitani, Langmuir 16, 6377 (2000)
W. A. Ducker, Langmuir 25, 8907 (2009)
M. P. Brenner and D. Lohse, Phys. Rev. Lett 101, 214505 (2008)
F. Jin, X. J. Gong, J. Ye, and T. Ngai, Soft Matter 4, 968 (2008)
K. Ohgaki, N. Q. Khanh, Y. Joden, A. Tsuji, and T. Nakagawa, Chem. Eng. Sci. 65, 1296 (2010)
X. H. Zhang, X. D. Zhang, J. L. Sun, Z. X. Zhang, G. Li, H. P. Fang, X. D. Xiao, X. C. Zeng, and J. Hu, Langmuir 23, 1778 (2007)

About the Author

Vince Craig is Head of the Department of Applied Mathematics at the Australian National University (ANU) in the Research School of Physics and Engineering. He completed both his B.Sc. (chemistry, 1993) and Ph.D. degrees (Research School of Physics, 1997) at the ANU before postdoctoral positions at the University of California, Davis, and the University of Newcastle, New South Wales. He is currently the recipient of an ARC Future Fellowship on the topic of specific ion effects. His other research interests include the direct measurement of surface forces, both quasistatic and dynamic, interfacial adsorption of surfactants and polymers, bubble coalescence in electrolyte solutions, and nanobubbles.