Light Control Takes Wing

Hailong Ning; Paul V. Braun

Viewpoint

Light Control Takes Wing

Hailong Ning and Paul V. Braun

Department of Materials Science and Engineering, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA

September 26, 2011• Physics 4, 76

Modified photonic structures from the wings of weevil beetles set a new record for optical emission control.

Figure caption — **Figure 1:** A diamond-structure photonic crystal strongly modifies the excited state lifetime ( $τ$ ) of quantum dots embedded in it. Dots that emit at frequencies where the structure has a photonic band gap (shown in blue) can have excited state lifetimes ten times longer than dots that emit at some other frequencies (red).

The fundamental principle governing radiative transitions is Fermi’s golden rule [1], which states that, ignoring nonradiative pathways, the excited-state decay rate is directly proportional to the photonic density of states (DOS). The photonic DOS is simply the number of electromagnetic modes available for the emitted photons to couple into. This leads to the obvious conclusion that optical emission can be directly controlled via manipulation of the DOS. Since 1987, when Yablonovitch and John first independently proposed the use of photonic crystals (PCs) to locally modify a material’s optical DOS and thus spontaneous emission (SE) [2], numerous groups have investigated this concept experimentally. In an article published in Physical Review Letters [3], Matthew Jorgensen and co-workers from the University of Utah in Salt Lake City demonstrate for the first time the strong impact of PCs with diamond-based symmetry on the SE of quantum dots over a wide frequency range. One unique aspect of this work is that these optically powerful PCs are derived from beetle shells. Thanks to the optical superiority of their diamond PC structure, the researchers see an unprecedented tenfold modulation of emission between enhanced and inhibited frequencies. This work may represent the next step towards controlling optical emission in three dimensions for applications including lasers and LEDs.

At its heart, a PC is a periodic material that can be thought of as an optical analog of a conventional atomic or molecular crystal. In PCs, however, the atoms or molecules are replaced by building blocks with contrasting optical constants ( $n$ and $κ$ ), and the periodicity, rather than being on the angstrom scale, is on the order of the wavelength of visible or infrared light. When the characteristic period of the structure is comparable with the wavelength of light and the refractive-index contrast is big enough, the propagation of light along a certain direction(s) can be completely inhibited for a range of frequencies, resulting in a so-called stop band. Moreover, when a specified frequency band lies within the stop bands for all directions in three-dimensional space, light of these frequencies is forbidden to travel in the crystal, resulting in a complete photonic band gap (PBG).

It is important to realize that PBGs only emerge for specific symmetries. Researchers have made significant efforts to discover and fabricate PCs with large PBGs. To date, diamondlike structures have been found to generate some of the largest gaps for a particular index contrast, and have received extensive attention for their “champion” photonic quality. The rod-connected diamond PC, a structure formed by dielectric rods that connect nearest-neighbor sites in the diamond lattice, exhibits an exceptionally broad gap width: $30 %$ of the mid-gap energy for a refractive-index contrast of $3.6$ [4]. Besides the large bandwidth, diamond-based PBGs, which open between low-energy bands, tend to be more immune to lattice defects compared to high-energy-band PBGs of other structures, such as those based on inverse opals [5]. (In inverse structures, the voids in a starting structure are filled with a different material, and the starting structure is typically removed.)

Although the combination of new theoretical designs and modern micro/nano fabrication techniques have realized a variety of highly functional PCs [6], fabricating diamondlike PCs operating in the visible spectrum remains challenging owing to their structural complexity, and previously had only been demonstrated through complex multistep e-beam lithographic techniques [7]. Nature, on the other hand, long ago developed an enormous palette of elaborate 3D PC architectures optimized for visible wavelengths. In particular, Galusha et al. recently discovered that the green coloration of one of the beetles of the weevil family comes from light reflecting from the diamond-based 3D PC structure of its exoskeleton [8]. Now this group has shown that the exoskeleton can be used as a template for high refractive-index-contrast structures. For a titania inverse PC, they calculate a complete PBG of $2.5 %$ in the visible. They probed the internal DOS of this high refractive-index-contrast PC structure using $CdSe / ZnS$ quantum dots (QDs) with a core-shell structure.

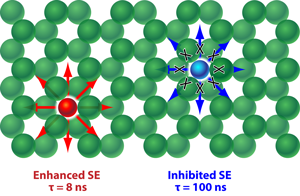
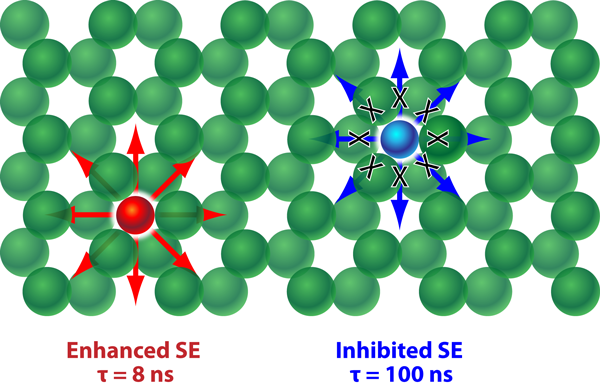
The emission spectrum of the core-shell emitters, which is broad enough to span the entire PBG, reflects the ensemble of the narrow emission lines of many individual QDs emitting at slightly different frequencies. The effectiveness of a full PBG on SE control is dramatically revealed after the infiltration of the PCs with these photon sources. At frequencies far outside the PBG, where the DOS is less-strongly modified by the PC (used as a reference), the SE decay rates of the QDs are found to be $0.071 \pm 0.005 {ns}^{- 1}$ (corresponding to an average lifetime of $14 \pm 1 ns$ ). The experiments reveal both strong emission inhibition (over a $10 %$ frequency band inside the PBG region where the DOS is low) and enhancement (at the low-frequency band edge where the DOS is high). As illustrated in Fig. 1, the measured radiative lifetimes range over a factor greater than $10$ , from $8 \pm 1 ns$ at the band edge (significant SE enhancement), to $99 \pm 2 ns$ within the PBG (significant SE inhibition).

A complete PBG forms due to overlapping stop bands along sets of symmetry-related principal directions that together prevent light from propagating in any direction. To examine if the overlap of stop bands is the decisive factor in strong SE inhibition, Jorgensen et al. studied the optical properties as they varied the refractive-index contrast. For the starting beetle-exoskeleton PCs, the low index contrast ( $\sim 1.5$ ), means the exoskeleton PCs do not possess a complete PBG, but according to photonic band structure simulations, they do present an overlap of multiple stop bands in some directions. Once QDs are embedded in these biological PCs, the researchers observe twofold SE inhibition. Although this inhibition is much less dramatic than when the same structure is inverted with high-index titania, it rivals that for opal PCs inverted with titania [9], demonstrating the enhanced modulation of the photonic DOS within the diamond structure relative to an inverse opal structure for a given refractive index contrast structure.

Jorgensen et al.’s experiments also reveal a strong nonexponential behavior of the SE decay and large distributions of decay rates at a given frequency, which is probably a result of the random positions of QD photon sources within the PC, each of which experiences a slightly different local photonic DOS. Rigorous quantification of the PC’s effect on SE will require control over the emitter location; when the emitter is randomly distributed through the structure, the SE decay will always be difficult to interpret. As Lodahl et al. described, a reference system, for example, a PC with the same structure and titania filling fraction but with a smaller lattice constant so that the emission is on the red side of the PBG, is also very helpful to rigorously quantify the effect of a PC on SE [9]. One exceptionally promising aspect of Bartl’s naturally derived PC is the degree by which its optical DOS is modulated despite it being a relatively low refractive-index-contrast system; much higher refractive index materials, for example, III-V semiconductors [10], are available, and even stronger light-matter interactions can be anticipated if beetle shells can be used as templates for these materials.

References

R. Loudon, The Quantum Theory of Light (Oxford University Press, New York, 2000)[Amazon][WorldCat]
E. Yablonovitch, Phys. Rev. Lett. 58, 2059 (1987); S. John, 58, 2486 (1987)
M. R. Jorgensen, J. W. Galusha, and M. H. Bartl, Phys. Rev. Lett. 107, 143902 (2011)
M. Maldovan and E. L.Thomas, Nature Mater. 3, 593 (2004)
A. Blanco, E. Chomski, S. Grabtchak, M. Ibisate, S. John, S. W. Leonard, C. Lopez, F. Meseguer, H. Miguez, J. P. Mondia, G. A. Ozin, O. Toader, and H. M. van Driel, Nature 405, 437 (2000)
K. A. Arpin, A. Mihi, H.T. Johnson, A. J. Baca, J. A. Rogers, J. A. Lewis, and P. V. Braun, Adv. Mater. 22, 1084 (2010)
G. Subramania, Y.-J. Lee, A. J. Fischer, and D. D Koleske, Adv. Mater. 22, 487 (2010)
J. W. Galusha, L. R. Richey, M. R. Jorgensen, J. S. Gardner, and M. H. Bartl, J. Mater. Chem. 20, 1277 (2010)
P. Lodahl, A. F. van Driel, I. S. Nikolaev A. Irman, K. Overgaag, D. Vanmaekelbergh, and W. L. Vos, Nature 430, 654 (2004)
E. C. Nelson, N. L. Dias, K. P. Bassett, S. N. Dunham, V. Verma, M. Miyake, P. Wiltzius, J. A. Rogers, J. J. Coleman, X. Li, and P. V. Braun, Nature Mater. 10, 676 (2011)

About the Authors

Hailong Ning is currently a Ph.D. candidate in materials science and engineering at the University of Illinois at Urbana-Champaign. He received his B.S. in optical physics from the Harbin Institute of Technology in China and M.S. in physics from the University of British Columbia in Canada. His research focuses on light matter interactions in three-dimensional periodic photonic structures.

Paul Braun is a professor of materials science and engineering at the University of Illinois at Urbana-Champaign. He received his Ph.D. in 1998, and following a postdoctoral appointment at Bell Labs, Lucent Technologies, he joined the faculty at Illinois in 1999. His group focuses on the synthesis and properties of 3D architectured materials that exhibit unique optical, electrochemical, thermal, and mechanical properties.