Spinning on Ice

Rajiv R. P. Singh

Viewpoint

Spinning on Ice

Rajiv R. P. Singh

Physics Department, University of California, Davis, CA 95616, USA

October 3, 2011• Physics 4, 77

A form of quantum electrodynamics emerges from interacting spins at low temperatures in the spin ice

{Yb}_{2} {Ti}_{2} O_{7}

.

Figure caption — **Figure 1:** (a) Spin configurations on a tetrahedra that obey the “ice-rules.” (b) Proposed low-temperature phases of a quantum spin ice consist of a magnetically polarized high-field phase with usual spin-flip excitations (shown at right) and a low-field phase consisting of “emergent” dynamical photons (shown by a wavy line) and electric and magnetic charges (shown schematically as plus and minus charges with emanating electric fields and north (N) and south (S) poles with emanating magnetic fields).

A spin ice is a three-dimensional network of corner-sharing tetrahedra with spins at the vertices. At low energies the spins obey “ice rules,” i.e., they point towards or away from the center of the tetrahedron in a two-in and two-out configuration, similar to positions of protons around an oxygen atom in ordinary ice. In a paper in Physical Review X, Kate Ross at McMaster University in Ontario, Canada, and collaborators report using inelastic neutron scattering in a strong magnetic field to determine the microscopic Hamiltonian for the spin-ice material ${Yb}_{2} {Ti}_{2} O_{7}$ [1]. They find a system with strong quantum fluctuations, which should give rise to a novel phase of matter, a kind of quantum spin liquid, in low magnetic fields. In such a phase, the original microscopic degrees of freedom, the spins, freeze out and instead only collective excitations of many spins remain active. The latter can be described as electric and magnetic charges and photons, the dynamical variables of a fictitious quantum electrodynamics.

A collection of spins in which each spin can fluctuate more or less independently is called a paramagnet and is analogous to a gas phase. A collection of spins that are frozen due to mutual interactions in a specific configuration with only harmonic fluctuations around that configuration, e.g., a ferromagnet or an antiferromagnet, is analogous to a solid phase. In contrast, spins that are strongly tied to their neighbors but continue to fluctuate in a cooperative manner are analogous to a liquid phase. The liquid phase has a much richer physics, and, like ordinary liquids, occurs only over a limited range of temperature. The cooperative dynamics can give rise to novel emergent behavior that, at first view, may appear unrelated to the microscopic constituents of the system.

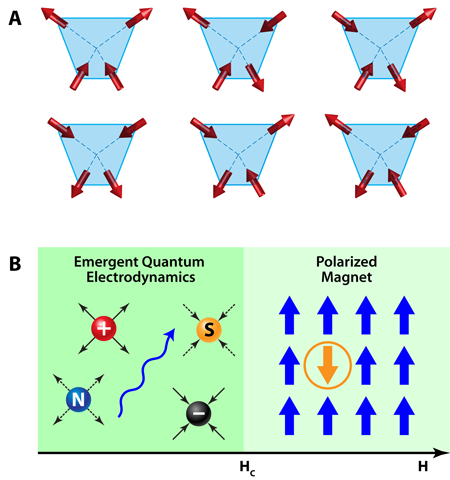
In spin-ice materials, anisotropy in the crystal structure constrains the spins on the vertices of the tetrahedra to point along the line that connects the vertex to the center [2]. At low temperatures, exchange and dipolar interactions further constrain the four spins in a tetrahedron in the configuration that has two spins pointing towards the center and two away from it [Fig. 1(a)]. From Pauling’s classic work [3] on ice, we know that the number of states that obey these “ice rules” grows exponentially with the size of the system and leads to finite entropy. Indeed, an early success in the study of spin ice was the determination of this entropy from measurements of specific heat [4].

The spin-ice materials that have been studied the most to date, ${Ho}_{2} {Ti}_{2} O_{7}$ and ${Dy}_{2} {Ti}_{2} O_{7}$ , are examples of classical spin liquids. In these materials, low-temperature behavior is indeed characterized by emergent degrees of freedom, as the spins cannot fluctuate independently and continue to satisfy the ice rules. Defects resulting from the violation of the ice rules lead to magnetic monopole excitations, which interact via the $1 / r$ Coulomb potential [5]. Their existence has been confirmed through a number of experiments [6]. But in these materials, the transition from one low-energy configuration to another occurs through thermally assisted processes, analogous to the situation in ordinary liquids like water. Such a system lacks quantum coherence, and it is appropriate to call it a classical spin liquid.

In contrast to these materials, ${Yb}_{2} {Ti}_{2} O_{7}$ and a few others like ${Er}_{2} {Ti}_{2} O_{3}$ are examples of a quantum spin ice. They are characterized by an effective spin-half degree of freedom and their nearest-neighbor exchanges dominate over the long-range dipolar interactions. Furthermore, various spin-flip parts of the exchange interaction, which can lead to quantum tunneling between different classical configurations, can be quite appreciable. Earlier work by Thompson et al. [7] used inelastic neutron scattering in zero field at relatively high temperatures to determine these exchange constants.

Kate Ross and her coauthors focus on inelastic neutron scattering data at low temperatures and high fields. At high fields, the system is adiabatically related to a fully polarized phase, where all the spins point along the field. This is confirmed by the very sharp dispersive spin-wave-like spectra seen in the experiments. This regime is also amenable to a semiclassical theoretical treatment, which allows them to calculate the dispersion of the spectral lines and spectral weights accurately, and compare with the experiments. The agreement for the best-fit exchange parameters is remarkably good throughout the Brillouin zone. This gives them confidence in their measurements.

Some of the spin-flip terms found in these materials are comparable to the classical terms responsible for the spin-ice constraint. These quantum mechanical processes can lead to two opposing tendencies at low temperatures. They can drive the system to a long-range ordered solid phase by lowering the energy of a particular configuration of spin ice more than the others. Or, they can lead to a highly resonating quantum spin-liquid phase [8]. It is worth remembering that quantum liquids are extremely rare indeed. As a material, helium is the only quantum liquid; all other materials freeze into a solid phase.

Hermele et al. [9], following earlier work by Huse et al. [10], demonstrated theoretically the existence of a quantum spin-liquid phase in a spin-ice model, by mapping to an exactly soluble quantum dimer problem [11]. They argued that in the vicinity of this soluble model there exists a special quantum phase with emergent gauge fields, photons, electric and magnetic monopoles [Fig. 1(b), left panel], and topological order [12]. Quantum Monte Carlo simulations confirmed the existence of such a phase [13]. However, the types of spin-flip terms in these materials are quite different from those studied in the simulations, and it remains to be seen if the specific model found by Ross et al. for ${Yb}_{2} {Ti}_{2} O_{7}$ can be efficiently studied by controlled numerical methods in zero field.

Ross et al. argue that ${Yb}_{2} {Ti}_{2} O_{7}$ should be a quantum spin liquid at low fields for two main reasons. First, their mean-field theory for an ordered state fails to describe the experiments. Second, at low fields the sharp dispersive modes give way to only diffuse neutron scattering, which implies an absence of conventional order and may reflect the emergence of new degrees of freedom, which do not couple to the neutrons in a simple way.

However, much work remains to be done. There is evidence of a finite-temperature anomaly in thermodynamic and spectral properties at a temperature an order of magnitude below the mean-field ordering temperature [1]. This is not yet understood. Also, in the case of a quantum spin liquid, there must exist a quantum phase transition that separates it from the high-field polarized phase [Fig. 1(b), right panel]. Such a phase transition has not been precisely located. Clearly, the diffuse neutron scattering in the low-field phase contains important clues and its quantitative understanding will be essential for establishing the quantum spin-liquid behavior. Thermodynamic and spectroscopic signatures of the emergent photon mode, if found, would also be really exciting. However, the possibility of a more conventional phase, with either impurities or frozen-in domain walls, or both, has also not been ruled out.

The quest for a quantum spin-liquid phase with emergent properties remains one of the key goals of the field. These materials add to a small but growing list of experimental candidates. Hopefully, definitive results on real quantum spin liquids are not far away.

Acknowledgment

Support from the National Science Foundation grant number DMR-1004231 is gratefully acknowledged.

References

K. A. Ross, L. Savary, B. D. Gaulin, and L. Balents, Phys. Rev. X 1, 021002 (2011)
J. S. Gardner, M. J. P. Gingras, and J. E. Greedon, Rev. Mod. Phys. 82, 53 (2010)
L. Pauling, J. Am. Chem. Soc. 57, 2680 (1935)
A. P. Ramirez et al., Nature 399, 333 (1999)
C. Castelnovo, R. Moessner, and S. L. Sondhi, Nature 451, 42 (2008)
T. Fennell et al., Science 326, 415 (2009)
J. D. Thompson et al., Phys. Rev. Lett. 106, 187202 (2011)
P. W. Anderson, Mater. Res. Bull. 8, 153 (1973)
M. Hermele, M. P. A. Fisher, and L. Balents, Phys. Rev. B 69, 064404 (2004)
D. A. Huse et al., Phys. Rev. Lett. 91, 167004 (2003)
D. S. Rokhsar and S. A. Kivelson, Phys. Rev. Lett. 61, 2376 (1988)
R. Moessner and S. L. Sondhi, Phys. Rev. B 68, 184512 (2003)
A. Banerjee et al., Phys. Rev. Lett. 100, 047208 (2008)

About the Author

Rajiv R. P. Singh is Professor of Physics at the University of California at Davis. He received his Ph.D. in physics in 1986 from the State University of New York at Stony Brook. He was then a postdoctoral researcher at Cornell University, at the University of Maryland, and at AT&T Bell Labs in Murray Hill, New Jersey. He joined the physics faculty at the University of California at Davis in 1989. He became a fellow of the American Physical Society in 2006. His research interests include studies of quantum phases of matter and biological physics.