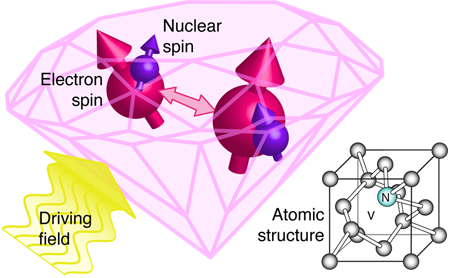
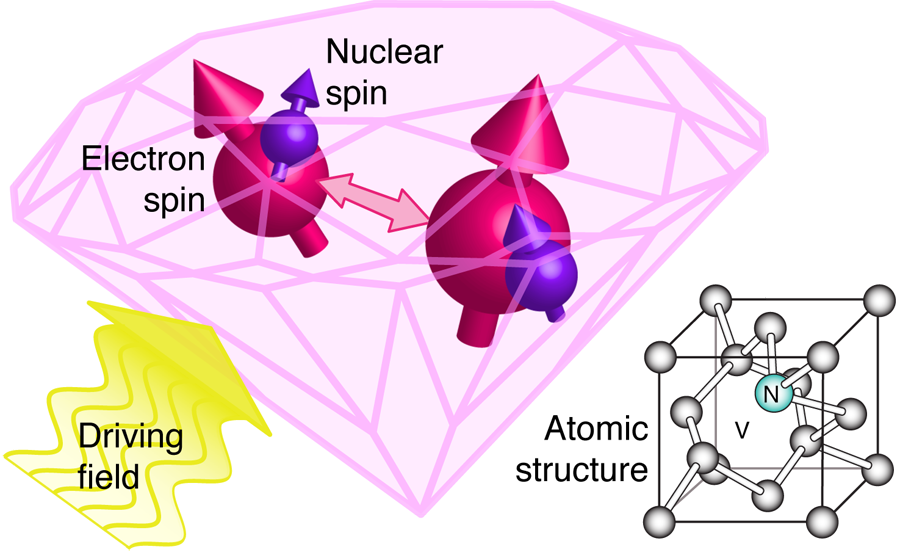
Driving a Hard Bargain with Diamond Qubits
The ideal building block or qubit for a quantum computer needs to possess several conflicting properties: it should be under precise control and yet almost perfectly isolated from its environment; it should be accessible separately from other components and yet coupled to them. A certain kind of impurity that occurs in diamond, called a nitrogen vacancy (NV) center, seems almost ideal, except that we don’t yet know how best to couple different sites. This is absolutely essential in order to achieve entanglement between the various qubits. Now, writing in Physical Review Letters, Alejandro Bermudez and colleagues at the University of Ulm, Germany, present a theoretical scheme to improve NV coupling that exploits the complex structure of the NV system, together with an external electromagnetic driving field [1]. Information is stored in a nuclear spin at each location, while their big brother electron spins enable site-to-site communication. This elegant idea may prove less difficult to implement than previous solutions. If so, it will overcome a major obstacle to diamond-based quantum information technology.
A NV center is a “color center,” which gives pink diamond its hue. The system forms when two different kinds of defect bind together on adjacent lattice sites: a nitrogen impurity and a vacancy (a missing carbon atom) (see Fig. 1, bottom right). The combined entity may trap an additional electron, becoming negatively charged. The six unbound electrons present (three from adjacent carbons, two from the nitrogen atom, plus the one that has been trapped) form a spin-triplet ground state with exquisite coherence properties, which can be both polarized and measured using straightforward optical methods, and manipulated by applied electric and magnetic fields. Moreover, the presence of the nitrogen atom (which has a nuclear spin of ) implies that each NV center must have at least one nuclear spin present. Nuclei are ideal for storage of quantum information, because of their long coherence times. NV centers also benefit from the extreme hardness of diamond, which corresponds to an unusual phonon spectrum and thus allows certain quantum properties to persist, even at room temperature. Thus the NV center appears exceptionally well-suited for quantum information handling, and the past few years have seen a number of landmark demonstrations, from two and three-qubit operations using neighboring electronic or nuclear spins [2–4] to entanglement between an electron spin and an optical photon [5].
How can we enable different NV centers to achieve entanglement with one another, and thus produce a scalable architecture with the potential to represent the thousands, or millions, of qubits required for general-purpose quantum computers? Various solutions have been proposed. In one family of ideas, it is the optical emission of the centers that is exploited [6]. By making a joint measurement on photons emitted from two sites, those sites can be projected into an entangled state. This solution would therefore involve an optical network of well-separated NV centers, which is attractive in terms of scalability and the freedom to control and measure each site separately. However, NV centers are far from ideal photon sources; only a fraction of emissions occur without an accompanying phonon, the absence of which is required to produce entanglement. Another recent idea [7,8] is to use a chain of “dark” spins—those on substitutional nitrogen atoms that do not have an adjoining vacancy—to link NV centers over distances of micrometers. The spins associated with such atoms are not optically active (and hence “dark”) but can nevertheless suffice to form a wire or “bus” between the active sites. But again, there are challenges: to date, no group has demonstrated the control needed to implant such a heterogeneous network.
The idea put forward by the Ulm team is simpler to express than these previous suggestions. Since the nuclear spin at each site (bearing a qubit) is able to “see” its local electron spin partner via the hyperfine interaction, it follows that if the electron spins at neighboring sites can interact sufficiently strongly, then the two nuclei will be able to communicate indirectly through their electron brothers. While the idea is simple, it turns out to be more complex than one might imagine, in fact, Bermudez et al. start by establishing that the electron-mediated interaction between nuclei at adjacent NV sites will be far too weak to be useful! They estimate that even quite closely neighboring sites, nanometers ( ) apart, will have an effective nuclear-nuclear coupling strength of only hertz—requiring several seconds to achieve a useful exchange of information. This is impractical, since nuclear spins suffer dephasing (losing any stored qubit) in less than a second.
Happily, the Ulm team has discovered a solution. Their analysis predicts that when the spins are resonantly driven by externally applied electromagnetic fields, the effective strength of the interaction increases dramatically. In essence, they introduce a new energy scale into the problem, replacing the effect of the crystal field splitting (which acts to suppress the effective nuclear-nuclear coupling) with the Rabi frequencies of the driven spins—a parameter that is under experimental control. Remarkably, with a suitable choice for this parameter, the coupling between nuclei is enhanced a thousandfold, becoming entirely practicable as a channel to exchange quantum information. As an added bonus, the act of driving the spins serves to protect the quantum state from the decohering effects of the surroundings. The effect is equivalent to “dynamic decoupling,” in which a spin that is periodically inverted at a frequency faster than the local magnetic field fluctuations acquires an aggregate zero phase [9].
Bermudez et al. have confirmed that their scheme should be possible with experimental conditions similar to those already achieved, in particular, in the work of Neumann et al. [10]. However, there are of course remaining challenges. To use this method to generate quantum entanglement on the sort of scale that would be useful for a general-purpose quantum computer would require a large array of NV centers. A recent study reports that positioning of individual centers can be achieved with about accuracy, using implantation of molecules through nanoapertures [11]. This is approaching “the ballpark” for the new scheme and the authors speculate that denser arrays will indeed be possible. Even so, questions remain as to how the individual addressing of NV centers in a large group will be possible. The use of magnetic field gradients to impart a spatial dependence of the Zeeman splitting may well be part of the solution, but is unlikely to be sufficient without further discrimination. Nevertheless, the challenges in developing diamond quantum computers are being overcome at an astonishing rate. Bermudez et al.’s idea for entangling two nuclear spins is a powerful and remarkably elegant new option.
References
- A. Bermudez, F. Jelezko, M. B. Plenio, and A. Retzker, Phys. Rev. Lett. 107, 150503 (2011)
- R. Hanson et al., Phys. Rev. Lett. 97, 087601 (2006)
- L. Childress et al., Science 314, 281 (2006)
- P. Neumann et al., Science 320, 1326 (2008)
- E. Togan et al., Nature 466, 730 (2010)
- S. C. Benjamin, B. W. Lovett, and J. M. Smith, Laser Photon. Rev. 3, 556 (2009)
- N. Y. Yao et al., Phys. Rev. Lett. 106, 040505 (2011)
- N. Y. Yao et al., arXiv:1012.2864v1
- G. de Lange et al., Science 330, 60 (2010)
- P. Neumann et al., Nature Phys. 6, 249 (2010)
- P. Spinicelli et al., New J. Phys. 13, 025014 (2011)