Forcing Tumor Arrest
In 1962, the cancer physician Sir David Smithers wrote a fierce attack on cytologism, saying “cancer is no more a disease of cells than a traffic jam is a disease of cars. … A lifetime of study of the internal-combustion engine would not help anyone understand our traffic problems” [1]. His view, that cancer was just as much about a cell’s interaction with its microenvironment as it was about the cell itself, was not new. The surgeon Stephen Paget had expressed it in 1889 in his famous “seed and soil” hypothesis of metastasis, which held that cancer cells could spread throughout the body, but not necessarily grow into a tumor unless the local microenvironmental conditions were favorable [2]. However, the discovery of the first oncogenes and tumor suppressor genes in the 1970s and 1980s [3] eventually overshadowed studies of the role of tumor microenvironment in cancer development. Today, the notion that genetic aberrations only lead to tumor growth and metastasis under specific microenvironmental conditions is gaining renewed interest. In a paper appearing in Physical Review Letters, Fabien Montel and colleagues at the Curie Institute in Paris present experiments in which they explore the effects of mechanical stress on the evolution of a tumorlike collection of cells [4]. Their work suggests that pressure may impede the growth of a tumor by altering the location and rates of cell division and cell death.
To a great extent, the influence of the microenvironment on cancer cell behavior is mediated by the composition, structure, and dimensionality of the extracellular matrix, the polymeric scaffold that surrounds cells within tissues. For example, a malignant phenotype can be reverted into a nonmalignant one by specifically blocking aberrant adhesion of the cancer cell to its extracellular scaffold [5]. Research has also found that the mechanical activity of the tumor microenvironment can facilitate or oppose tumor growth and dynamics, though this effect is poorly understood. Mechanical stresses such as those experienced by cancer cells during the expansion of the tumor against the stromal tissue have been shown to release and activate growth factors involved in the progression of cancer. Moreover, the stiffness of the matrix surrounding a tumor determines how cancer cells polarize, adhere, contract, and migrate, and thus regulates their invasiveness [6].
The mechanical activity of a tumor’s microenvironment may alter its growth through diverse mechanisms. Some of these mechanisms involve the transduction of physical forces into chemical signals [7]. Yet another possibility is that mechanical stresses directly regulate the growth and death rates of cancer cells. It is this possibility that Montel et al. have explored in their current work.
As a simple experimental model, the authors used mouse cells that self-assemble into tumorlike spheroids. Although these spheroids are similar to tumors, they have a much simpler structure and composition. In the absence of any external stress, these spheroids grow in size over two or three weeks until they reach a steady state where the rate of cell division is balanced by the rate of cell death. Montel et al. hypothesized that this steady state could be altered if the spheroids were held under an applied mechanical stress.
How can a physically meaningful and mechanically uniform stress be applied to a growing tumor spheroid? One possibility is to grow the spheroids under hydrostatic pressure [8], another is to grow them in the presence of gels of varying stiffness that oppose tumor expansion [9]. Montel et al. have chosen to use a new and simpler method that opposes the expansion of the tumor. They apply an osmotic stress by increasing the molecular concentration of the medium surrounding the spheroid. The group used dextran to create this osmotic pressure, since it is a biocompatible polymer that is not metabolized by cells and does not affect their viability.
Montel et al. designed two different experimental strategies. In the direct strategy, the tumor spheroid was directly subjected to an osmotic pressure, in such a way that the outer layer of cells was in direct contact with the dextran. To ascertain that this direct contact did not affect the experimental outcome, they also used an indirect strategy in which the spheroid was enclosed in a dialysis bag with a pore size that was smaller than the size of dextran molecules. Under these conditions, the mechanical stress was fully transmitted to the spheroid surface, but the outer cell layer was never in contact with dextran. In both approaches, the results were similar: an external osmotic stress as weak as pascals slowed down the growth rate of the tumor spheroid. This process is also reversible, meaning that once the pressure is released, the spheroid can grow again.
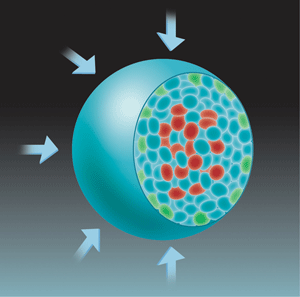
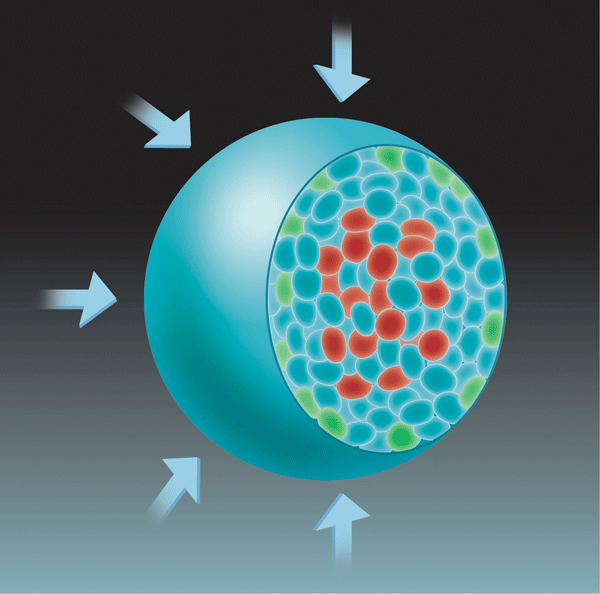
For tumors to grow, cells must divide faster than they die. To test the possibility that mechanical stress was enhancing cell death relative to cell division, the authors mapped the sites of both processes within the spheroid. Consistent with earlier work [10], they found that cell death was mostly localized at the center of the spheroid, but cell division was localized both at its center and at its growing edge (Fig. 1). Although applying a mechanical stress did not alter the location of cell death, it did restrict cell division to the growing edge of the spheroid.
To interpret their results, the authors propose a simple model based on growth rates that are dependent on the applied stress and on the cell location within the spheroid. Specifically, the growth rate at the edge of the spheroid is assumed to be larger than the bulk growth rate by an additive term , and both and are allowed to have a different dependence on stress. A master equation describing this growth predicts how spheroid volume changes with time, and can be used to fit the experimental data and obtain the actual variation of growth rates with external stress. These fits show the dependence of on mechanical stress is much weaker than that of , which is consistent with numerical simulations based on purely physical considerations.
The authors’ findings could, in principle, be explained by purely chemical arguments. It is well known that osmotic stresses can alter cell metabolism through biochemical stress-response pathways [11]. However, the authors argue that this effect only occurs at dextran concentrations orders of magnitude higher than those used in their study. An alternative explanation to the author’s findings would be that osmotic stress reduces the transport of nutrients and growth factors to the center of the spheroid, which prevents cells from dividing. The authors ruled out this possibility by showing osmotic stress doesn’t block the transport of a fluorescently labeled molecule to the center of the spheroid. Taken together, these findings suggest it is truly a mechanical effect that is suppressing the tumorlike growth.
Montel et al.’s study was aimed at testing a general theoretical framework for tumor growth that they proposed recently [12]. This theoretical framework assumes tissues exist in a homeostatic state that generally depends on local concentrations of soluble molecules (e.g., nutrients, vitamins, growth factors) and oxygen, as well as on mechanical and biochemical signals from the local microenvironment. Within this model, aberrant tissue growth is a consequence of an increase in homeostatic pressure, which can be mediated by a variety of microenvironmental factors. The strength of this model lies in its generality. Rather than focusing on one specific chemical or physical variable, the model can explicitly integrate diverse variables that may lead to an increase in homeostatic pressure and subsequent tumor growth. Montel et al.’s findings provide additional experimental support to this theoretical framework, which now emerges as a promising tool for understanding the effect of the microenvironment during tumor growth.
References
- D. W. Smithers, Lancet 1, 493 (1962)
- J. E. Talmadge and I. J. Fidler, Cancer Res. 70, 5649 (2010)
- E. Y. Lee and W. J. Muller, Cold Spring Harb. Perspect. Biol. 2, 003236 (2010)
- F. Montel, M. Delarue, J. Elgeti, L. Malaquin, M. Basan, T. Risler, B. Cabane, D. Vignjevic, J. Prost, G. Cappello, and J-F. Joanny, Phys. Rev. Lett. 107, 188102 (2011)
- V. M. Weaver, O. W. Petersen, F. Wang, C. A. Larabell, P. Briand, C. Damsky, and M. J. Bissell, J. Cell Biol. 137, 231 (1997)
- M. J. Paszek, N. Zahir, K. R. Johnson, J. N. Lakins, G. I. Rozenberg, A. Gefen, C. A. Reinhart-King, S. S. Margulies, M. Dembo, D. Boettiger, D. A. Hammer, and V. M. Weaver, Cancer Cell 8, 241 (2005)
- B. D. Hoffman, C. Grashoff, and M. A. Schwartz, Nature 475, 316 (2011)
- G. Cheng, J. Tse, R. K. Jain, and L. L. Munn, PloS ONE 4(2), e4632 (2009)
- G. Helmlinger, P. A. Netti, H. C. Lichtenbeld, R. J. Melder, and R. K. Jain, Nat. Biotechnol 15, 778 (1997)
- W. Mueller-Klieser, Am. J. Physiol. Cell Physiol. 273, C1109 (1997)
- M. B. Nielsen, S. T. Christensen, and E. K. Hoffmann, Am. J. Physiol. Cell Physiol. 294, C1046 (2008)
- M. Basan, T. Risler, J. F. Joanny, X. Sastre-Garau, and J. Prost, HFSP J. 3, 265 (2009)