Recreating a Stellar Electron Catch

Karlheinz Langanke

Viewpoint

Recreating a Stellar Electron Catch

GSI Helmholtzzentrum für Schwerionenforschung GmbH, Planckstrasse 1, 64291 Darmstadt, Germany
Technische Universität Darmstadt, Karolinenplatz 5, 64289 Darmstadt, Germany

November 7, 2011• Physics 4, 91

Experimentalists can now determine rates of electron capture in unstable nuclei, providing crucial information for star collapse simulations.

Figure caption — **Figure 1:** Schematic of the nuclear transitions involved in electron capture, and its inverse, in a nickel- $56$ nucleus, which result in a cobalt- $56$ (one less proton) or a copper- $56$ (one more proton) nucleus, respectively. The transitions between single-particle states shown here is an over-simplified representation of the actual many-body process.

The energy scales involved in the capture of electrons by nuclei in a star are vastly different than those of atoms. While the latter can be studied in a table-top experiment, large facilities are needed to explore this fundamental nuclear process. Now, a team of scientists (Sasano et al.) working at the National Superconducting Cyclotron Laboratory at Michigan State University has measured an important electron capture process in nickel- $56$ that will help to improve simulations of stellar evolution in the late stages of burning [1]. The results, which are reported in Physical Review Letters, settle an important debate about how best to model nuclear structure in such simulations and represent the first implementation of a technique likely to be applied at radioactive ion-beam facilities currently being planned around the world.

At the end of its burning stages, a massive star has an onionlike structure: nuclear burning still proceeds in the outer layers, while the central core has no nuclear energy source to support itself against gravitational collapse. The core composition is made of nuclei—initially in the iron-nickel mass range—and electrons. While the nuclei make up most of the core’s mass (about $1.5$ times the mass of the sun), it is the electrons, which form a degenerate, relativistic gas, that provide the outward pressure against gravitational collapse. With increasing density and temperature, the Fermi energy of this electron gas grows, reaching of order $MeV$ and higher during the final seconds of the collapse.

At such high energies, the weak force enables protons bound in the nuclei to capture electrons from the gas and turn into neutrons, emitting neutrinos in the process [2]. This conversion reduces the electron degeneracy pressure and the star’s core temperature, since neutrinos can, in the initial phase of the collapse, leave the star unhindered and carry away energy. Both effects accelerate the star’s collapse, leading to a type-II supernova [3]. As protons become neutrons, the nuclear composition of the star also changes, ultimately becoming dominated by unstable neutron-rich nuclei in the later stage of its collapse.

Simulating this stellar process requires reliable inputs of the relevant nuclear reactions. At the finite temperatures found in stars, nuclei exist as a thermal ensemble. These thermally populated states have lifetimes that are too short for electron capture to be measured experimentally; rather, the process has to be modeled. Under stellar conditions, electron captures are usually dominated by so-called Gamow-Teller ( ${GT}_{+}$ ) transitions, in which a proton is changed into a neutron and, to conserve angular momentum, the spin of the nucleon can change by one unit, the total value carried by the captured electron and the emitted neutrino. In this process, the ${GT}_{+}$ transitions connect the parent state to many possible daughter states. To correctly reproduce this “fragmentation” over many final states (which is called the GT strength function) requires an accurate description of the correlations between nucleons. Nuclear shell-model calculations do this by including a residual interaction, which accounts for correlations among the neutrons and protons that occupy well-defined single-particle states [4]. Shell-model calculations reproduce GT strength functions and low-energy spectra of nuclei in the iron-nickel mass range quite well [5,6], providing the necessary electron capture input to late-stellar evolution and core-collapse supernovae with important impact on the temperature, composition, and size of the collapsing iron core [7,8].

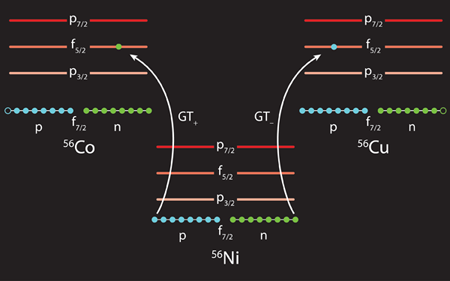
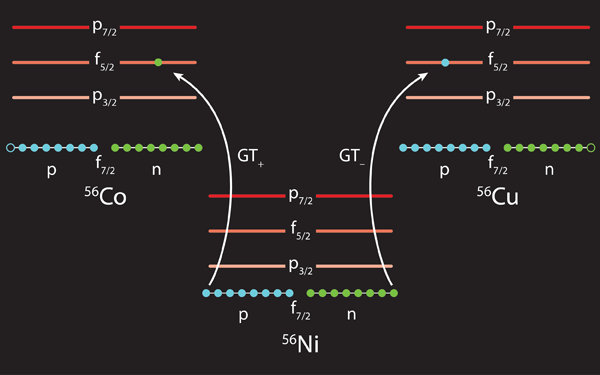
Shell-model calculations have to be verified with actual measurements of the ground-state ${GT}_{+}$ distributions. Nickel- $56$ , an unstable isotope of nickel with a half-life of six days, is an important test case. This isotope is said to be doubly magic because eight protons and eight neutrons fill the outer shells—a relatively stable configuration. In an electron capture process, a proton in the outer shell is changed into a neutron in the same energy shell (Fig. 1). Early work [6] predicted that because nickel- $56$ is doubly magic, it would have a different GT distribution than for most other nuclei [4]; i.e., despite the strong correlations among nucleons, the GT strength is expected to reside mainly in one strong transition rather than being fragmented over many states. However, a more recent model that includes a novel residual interaction predicts the GT-transition strength in nickel- $56$ [9] is fragmented like in other nuclei in its mass range.

Sasano et al.’s measurement of the nickel- $56$ GT distribution now settles the disparity between the different predictions [1]. In the experiment, they bombard a hydrogen target with a beam of nickel- $56$ nuclei. The fact that this setup yields information about electron capture makes use of two important relationships. First, the strength of ${GT}_{+}$ and the reverse transition, ${GT}_{-}$ , where a neutron is changed into a proton, are nearly the same for nuclei with equal numbers of protons and neutrons, like nickel- $56$ . So, in fact, the group measured the ${GT}_{-}$ distribution. Second, the ${GT}_{-}$ strength is proportional, within a normalization constant and under certain scattering conditions, to the cross section for a nucleus (in this case nickel) to absorb a proton (and emit a neutron). The relationship is fortuitous, since even though both processes have the same initial and final nuclear states, the latter process is driven by the strong interaction, while electron capture is a weak-interaction process. Similar techniques have been widely used to measure GT transitions in stable nuclei [10], but to study the same process in an unstable nucleus like nickel- $56$ requires a switch of target and projectile, which is only possible at a facility that can accelerate heavy, radioactive nuclei.

The measurement shows that the GT strength is strongly fragmented over many states in the daughter nucleus. In fact, the data agree nicely, except for an overall energy shift of about $0.5 MeV$ , with the prediction of the new residual shell-model interaction.

As a proof of principle, Sasano et al.’s work shows there is an experimental technique that can measure the GT- strength distribution for unstable isotopes—a method that will come into play at next-generation radioactive ion-beam facilities. GT- distributions do not directly constrain electron capture rates, but they are relevant for the determination of half-lives, beta-delayed neutron emission rates, or neutrino-induced cross sections as they are needed in simulations of the astrophysical rapid neutron capture process that is believed to play a role in the synthesis of heavier elements.

Astrophysical electron capture rates for nickel- $56$ derived from shell-model calculations with the two different residual interactions differ by as much as $30 %$ [9]. This is probably too small an effect to have a significant impact on late stellar evolution, but has to be tested in simulations. Furthermore, Sasano et al.’s data are an important constraint to systematically improve shell-model estimates for the capture rates of other nuclei in the iron-nickel mass range that are present in the core of a collapsing star.

Finally, it will be interesting to compare the GT distribution for nickel- $56$ with that of its heavier sister, tin- $100$ . From a shell-model point of view, both nuclei are quite similar, only shifted by one major shell. For tin- $100$ , shell-model calculations predict the GT strength to reside in a single state, which, in contrast to nickel- $56$ , is accessible in its weak-interaction (beta) decay. This prediction has been tested in a beta-decay experiment performed at GSI, the heavy-ion facility in Darmstadt, Germany. The data are currently being analyzed. The Sasano et al. experiment is an exciting example of the new insights into nuclear structure one can expect from next-generation radioactive ion-beam facilities. Greater confidence in the inputs to astrophysical simulations will usher in a new era in nuclear astrophysics.

References

M. Sasano et al., Phys. Rev. Lett. 107, 202501 (2011)
G. M. Fuller, W. A. Fowler, and M. J. Newman, Astrophys. J. 252, 715 (1982)
H.-Th. Janka et al., Phys. Rep. 442, 38 (2007)
E. Caurier et al., Rev. Mod. Phys. 77 427 (2005)
E. Caurier, K. Langanke, G. Martínez-Pinedo, and F. Nowacki, Nucl. Phys. A653, 439 (1999)
K. Langanke and G. Martínez-Pinedo, Nucl. Phys. A673, 481 (2000); At. Data Nucl. Data Tables 79, 1 (2001)
A. Heger, S. E. Woosley, K. Langanke, and G. Martínez-Pinedo, Astrophys. J. 560, 307 (2001)
R. W. Hix et al., Phys. Rev. Lett. 91, 201102 (2003)
T. Suzuki et al., Phys. Rev. C 83, 044619 (2011)
Y. Fujita, B. Rubio, and W. Gelletly, Progr. Part. Nucl. Phys. 66, 549 (2011)

About the Author

After several years at Caltech and the University of Aarhus in Denmark, Karlheinz Langanke now heads the Research Division at GSI and is Professor for Theoretical Physics at the Technical University of Darmstadt. His research interests are in low-energy nuclear physics and nuclear astrophysics.

Gamow-Teller Transition Strengths from ${}^{56}{Ni}$

M. Sasano, G. Perdikakis, R. G. T. Zegers, Sam M. Austin, D. Bazin, B. A. Brown, C. Caesar, A. L. Cole, J. M. Deaven, N. Ferrante, C. J. Guess, G. W. Hitt, R. Meharchand, F. Montes, J. Palardy, A. Prinke, L. A. Riley, H. Sakai, M. Scott, A. Stolz, L. Valdez, and K. Yako

Phys. Rev. Lett. 107, 202501 (2011)

Published November 7, 2011

Read PDF