Hybrid Atom-Optomechanics
Researchers have used laser fields for decades to achieve extraordinary control over the quantum states of atoms, molecules, and ions. Condensed-matter physicists have recently made fast progress in achieving a similar level of control over nano- and micromechanical oscillators, i.e., lithographically engineered structures. Among the opportunities that drive this effort is the possibility of detecting and controlling these devices at the quantum level. Reaching this quantum regime makes it possible to prepare the mechanical oscillator in pure quantum states and observe how it evolves under interaction with the environment, potentially revealing yet unobserved decoherence mechanisms. From an applied perspective, such studies may also enable researchers to create sensors with improved sensitivity.
What makes mechanical systems attractive in this context is the large mechanical quality factor of micro- and nanomechanical systems (that is, their ability to store energy in resonant states for very long periods). One especially interesting case is silicon nitride [1]: membranes made of this material exhibit dissipation mechanisms that are surprisingly reduced and the subject of much research [2]. Building upon this earlier work with silicon nitride, Stephan Camerer from Ludwig Maximilians University, Germany, and colleagues report in Physical Review Letters [3] their progress in achieving atomic-mechanical coupling.
One method to achieve such control, which has recently been widely explored, consists of coupling the mechanical motion parametrically to an optical or microwave cavity mode, a technique first envisioned by Braginsky [4]. Indeed, optomechanical coupling allows substantial control of the mechanical oscillator state, including quantum-limited readout of its position and the preparation of the oscillator with very low residual thermal motion. The result is a mechanical oscillator that spends a significant fraction of its time in the quantum ground state. Despite the impressive progress made in cavity optomechanics [5,6] these schemes are approaching but not quite at the level of control that can be attained in atomic physics. In a different experiment, O’Connell et al. used a microwave field to mediate the coupling of a superconducting qubit to a high-frequency piezoelectric mechanical oscillator [7], enabling the intriguing observation of the swapping of quantum states between the qubit and the oscillator.
More generally, coupling the mechanical device to a fully controlled quantum system appears to be a promising route. Among the many proposals for such hybrid quantum systems, experiments that use ultracold atoms as the quantum “handle” on the mechanics are particularly attractive. Theorists have put forward a number of proposals of how atomic systems—such as a trapped ion [8–10], atom [11], Bose-Einstein condensate (BEC) [12], or atomic ensemble [13–15]—could be coupled to a mechanical device.
In the group of Theodor Hänsch, Philipp Treutlein and his colleagues at Ludwig Maximilians University have pioneered the practical implementation of such proposals. Recently, they have demonstrated the coupling of a BEC to a micromechanical cantilever via surface forces [16]. On their handy “atom-chips,” they managed to probe the motion of a micromechanical cantilever with a BEC approached to its surface. The oscillations of the cantilever caused a clearly discernable loss of atoms when it resonated with modes in the BEC; however, the backaction of the atoms on the mechanical motion could not be observed. The backaction in this case is the force that the atoms exert via the light field on the mechanical oscillator; it is precisely this backaction that mediates the mutual coupling between the two systems.
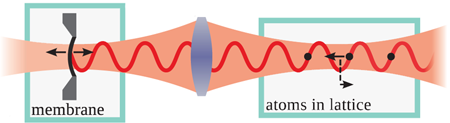
In the new work reported by Camerer et al. [3], this group accomplishes the feat of seeing the backaction (see Fig. 1) by elegantly implementing atomic-mechanical coupling via shared optical forces. The two coupled systems are an ensemble of about a million optically trapped atoms and a nanomechanical oscillator, consisting of a -nanometer, thin silicon nitride membrane mounted like a drumhead on a -millimeter silicon frame. These oscillators have dramatically different masses, with the membrane’s mass exceeding the mass of all atoms by about orders of magnitude. It is a surprisingly simple trick that allows coupling these two oscillators: The optical standing wave that provides the atoms’ lattice trapping potential is created by (partially) reflecting a laser beam from the membrane instead of a fixed mirror. From an experimentalist’s point of view, this is an intriguing arrangement [13], as the light used for coupling can be shuttled over a long optical path to connect the two subsystems, which can consequently be held in completely different environments.
But how does it work? In the first place, the standing wave, in whose antinodes the atoms are held, moves along with the membrane (Fig. 1). Therefore, if the membrane is moving, a force is exerted on the atoms proportional to the membrane’s displacement. At the same time, atomic motion does act back on the membrane: By its very nature, the optical trap forces each atom back to its equilibrium position if it moves out of the trap center. Importantly, however, the origin of this force is a redistribution of photons between the running-wave components that form the standing wave. As a consequence, the optical power propagating towards the membrane is modulated, and so is the radiation-pressure force on the membrane. Indeed, if optical losses and the finite transmission of the membrane are neglected, the forces experienced by the displaced atom and the membrane are exactly equal in magnitude, following the action-reaction principle.
The mutual coupling of membrane and atomic motion resulting from these forces becomes particularly clear if only the atomic center-of-mass mode—in which all atoms move in unison in (ideally) identical trapping potentials—is considered. The atomic motion and the membrane’s displacement then form a pair of optically coupled harmonic oscillators, with the coupling forces enhanced by the number of atoms in the lattice.
In their study, the authors could detect this coupling by investigating the damping induced upon the membrane by the atoms. As the atoms are cooled by another laser field (and additionally undergo dephasing), their motion is damped at a much higher rate ( kilohertz) than the oscillations of the membrane ( hertz). By tuning the two oscillators into resonance (choosing the appropriate optical power), an increase of the membrane damping was clearly observed, following the expected linear dependence on the atom number . A more elaborate model, taking into account the finite temperature of the atoms and the different trapping frequencies of atoms at different locations, could also fully reproduce the damping measured when the trapping frequency is tuned away from this degeneracy resonance.
In a second set of experiments, the researchers switched off the laser cooling of the atoms, and the mechanical mode of the membrane was excited by a piezoelectric transducer. The resulting heating of the atoms—with excitations of the center-of-mass mode quickly redistributed among their motional degrees of freedom—was measured. Again, resonant heating was observed when the “oscillators” were degenerate.
In future work, larger coupling would allow the full quantum control made possible by the atoms, which can be prepared in nonclassical states. Stronger coupling may be realized by using more atoms, placing the membrane in a cavity, or by using a different coupling arrangement, which overcomes the scaling with the square root of the mass ratio [11]. Moreover, the mechanical decoherence, i.e., the rate at which one quantum is lost to the environment, can be reduced. This rate, given by the energy damping multiplied by the mean phonon occupancy, can be decreased for silicon nitride by cryogenic precooling. The remote coupling demonstrated by Camerer et al. could be an enabling step in this context. It may then become possible to fully exploit the quantum coherent coupling between an atomic cloud and a micromechanical oscillator, and allow quantum control of solid-state systems.
References
- J. D. Thompson et al., Nature 452, 72 (2008)
- I. Wilson-Rae et al., Phys. Rev. Lett. 106, 047205 (2011)
- S. Camerer, M. Korppi, A. Jöckel, D. Hunger, T. W. Hänsch, and P. Treutlein, Phys. Rev. Lett. 107, 223001 (2011)
- V. B. Braginsky and A. B. Manukin, Measurement of Weak Forces in Physics Experiments, edited by David H. Douglass (University of Chicago Press, 1977)[Amazon][WorldCat]
- T. J. Kippenberg and K. J. Vahala, Science 321, 1172 (2008)
- F. Marquardt and S. Girvin, Physics 2, 40 (2009)
- A. D. O’Connell et al., Nature 464, 697 (2010)
- D. Wineland et al., J. Res. Natl. Inst. Stan. Technol. 103, 259 (1998)
- L. Tian and P. Zoller, Phys. Rev. Lett. 93, 266403 (2004)
- W. K. Hensinger et al., Phys. Rev. A 72, 041405 (2005)
- K. Hammerer et al., Phys. Rev. Lett. 103, 063005 (2009)
- P. Treutlein, D. Hunger, S. Camerer, T. Hänsch, and J. Reichel, Phys. Rev. Lett. 99, 140403 (2007)
- K. Hammerer et al., Phys. Rev. A 82, 021803 (2010)
- C. Genes, D. Vitali, and P. Tombesi, Phys. Rev. A 77, 050307 (2008)
- D. Meiser and P. Meystre, Phys. Rev. A 73, 033417 (2006)
- D. Hunger et al., Phys. Rev. Lett. 104, 143002 (2010)