Seeing Topological Order

Gediminas Juzeliūnas; Ian Spielman

Viewpoint

Seeing Topological Order

Gediminas Juzeliūnas

Institute of Theoretical Physics and Astronomy of Vilnius University, A. Goštauto 12, Vilnius 01108, Lithuania

Ian Spielman

Joint Quantum Institute, National Institute of Standards and Technology, and University of Maryland, Gaithersburg, MD 20899, USA

November 28, 2011• Physics 4, 99

Theorists propose a recipe for directly measuring the topological order in non-interacting cold atom systems.

Figure caption — **Figure 1:** A model system for seeing topological order. (a) Geometry of a Haldane-style lattice with two interpenetrating triangular lattices. Atoms in internal state A occupy one sublattice; atoms in internal state B occupy the other sublattice. A laser can induce a complex valued hopping $t exp (i ϕ)$ (dashed links, $ϕ$ is the phase of the laser) to form topological order (i.e., a nonzero Chern number) for the lattice. (b) Alba *et al.*’s prediction of the spin projection along $e_{x}$ , $e_{y}$ , and $e_{z}$ for this system, which can be measured with a time-of-flight experiment. The Chern number can be computed from the spin projections. (Spin projections were calculated by Ian Spielman, assuming $t / t_{a} = 2$ and $ϕ = 2 π / 3$ .)

Phases of matter are often described by an order parameter. For example the spins in a ferromagnet are randomly oriented at high temperature, but as the temperature falls below the Curie temperature, the spins begin to line up. A local order parameter given by the magnetization (the average spin density), distinguishes the normal and ferromagnetic phases. In contrast, topological insulators represent a broad class of band insulators distinguished not by local order but by global topological properties [1]. In analogy with order parameters in the usual study of phases and phase transitions, topological phases are distinguished by topological invariants, but the lack of local order makes it difficult to experimentally distinguish between different topological phases. Now, a theoretical paper appearing in Physical Review Letters from Emilio Alba at the Instituto de Física Fundamental, Spain, and his colleagues describes how the usually hidden topological order that can occur in certain cold atom lattices could be measured directly [2].

To get a feel for what a topological invariant is, consider Gauss’ law, in its integral form:

If $S$ is a surface enclosing $N$ electrons, the integral of the electric field over $S$ is independent of the configuration of the electrons, or even the shape of the surface, provided the electrons remain inside the volume enclosed by this surface. This is the essence of a topological invariant, which in this example, is simply a count of the fundamental charges. Building on this analogy, the so-called Chern number, $ν$ , of a topological insulator also results from the surface integral of a vector field and counts the “topological charge” contained within this surface.

The quantized Hall conductance of a two-dimensional semiconductor in a high magnetic field was the first measured example of topological order [3]. In fact, the quantized Hall conductance provides an indirect measure of the Chern number for these topologically ordered systems. However, finite temperature, disorder or the peculiarities of the semiconductor’s band structure obscure the relationship between what can be measured (the Hall conductivity) and the Chern number

Ultracold atoms in optical lattice traps represent a new platform to study topological matter. Optical traps are highly tunable, which means they can be engineered to match theoretical proposals for systems with a nonzero Chern number [4]. But even if experimentalists can prepare such a lattice, they need a measurable way to confirm that topological order exists. What Alba et al. have shown is that the Chern number for ultracold atoms that form a spin-dependent lattice can be determined directly from so-called time-of-flight measurements, where atoms are released from a trap and allowed to ballistically expand, so that their initial momenta can be determined from their final positions. Using their definition, a combination of the measurement tools and control at the quantum level that now exist would allow experimentalists to obtain the Chern number directly from systems of ultracold atoms.

Alba et al.’s proposal is rooted in the idea of Berry’s phases. Particles with internal structure (like spin) acquire a phase, called the Berry’s phase [5], when they move in a magnetic field that varies slowly in space. Mathematically, this means the parameters in the Hamiltonian describing the particles are slowly changing. If a particle starts in an eigenstate, it can acquire a phase upon traversing a closed loop in parameter space, provided the “motion” is sufficiently slow that it adiabatically returns to the same eigenstate. This phase is qualitatively the same as the Aharonov-Bohm [6] phase of a charged particle moving in a magnetic field. It results from a fictitious vector potential $A (q)$ , called the Berry connection, or from the associated field $B (q) = \nabla_{q} \times A (q)$ , known as the Berry curvature.

Systems with topological order are defined by having a nonzero flux of the Berry curvature over the surface. In two-dimensional materials, the definition of the Chern number has a close analogy with Gauss’ law:

Here, the integration is not performed in real space, but instead the “volume” enclosed is the 2D Brillouin zone of the lattice, and the vector field is determined by the Berry connection $A (q)$ , defined through the band eigenstates with crystal momentum $q$ . In other words, the Chern numbers represent the “flux” of the Berry curvature through the first Brillouin zone, and like the charges in the electrostatic analogy, this flux is quantized.

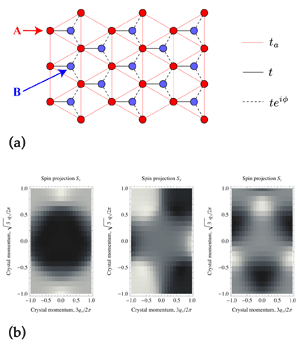
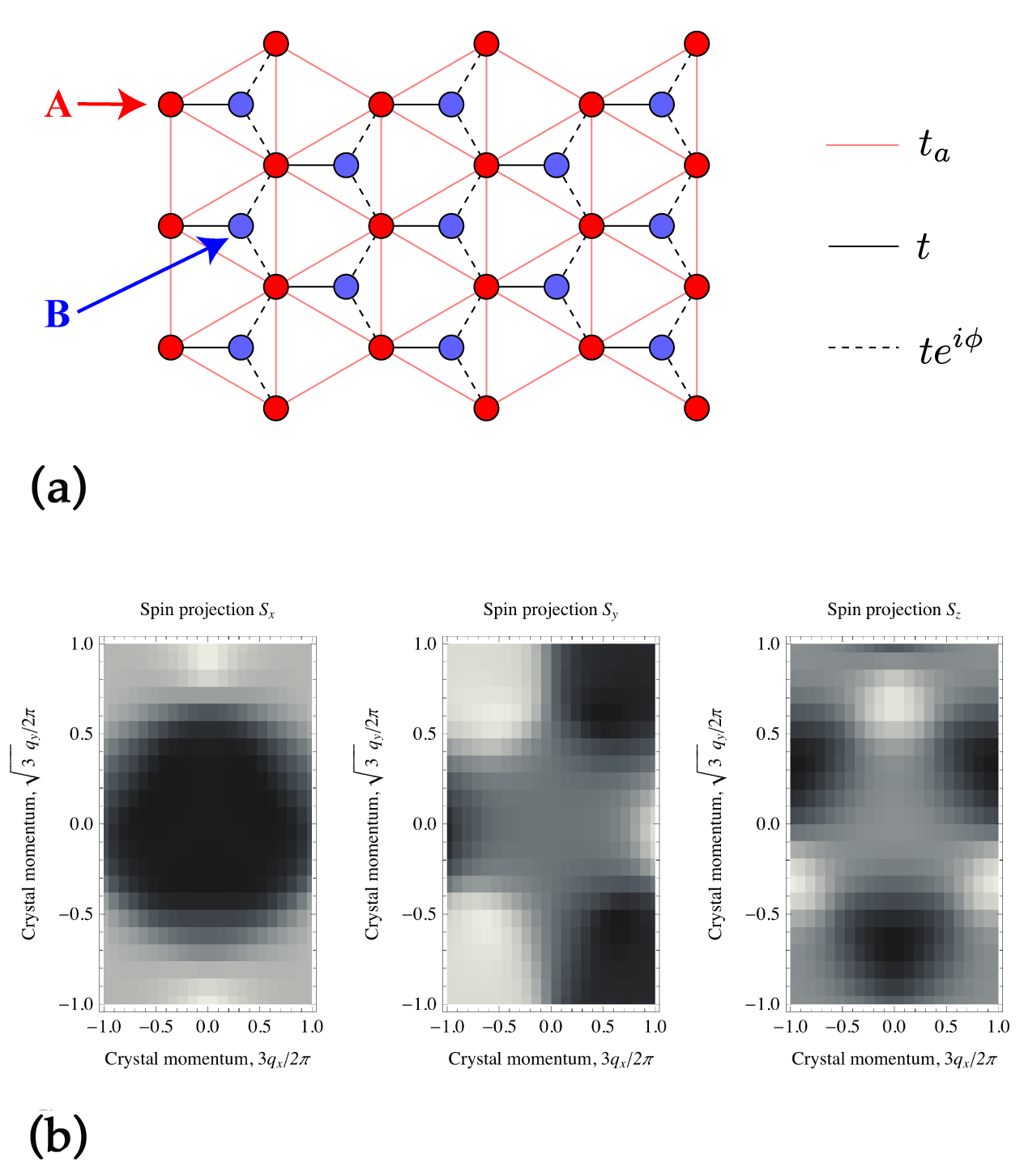
In 1988, F. Duncan M. Haldane noticed that a hexagonal lattice with additional next-nearest hopping with nonzero phases can lead to a unit Chern number [7]. Now Alba et al. consider a variant of the Haldane model [Fig. 1(a)], which can be implemented for cold atoms with two internal states. They assume that the atoms in each of these states are trapped at the sites of two triangular sublattices, making a hexagonal lattice. They also assume that laser-assisted tunneling can link the internal states of atoms that occupy neighboring sites. This ensures that the tunneling of atoms between the two sublattices is described by complex valued matrix elements [4]. Alba et al. show that when tunneling between next-nearest neighbor sites (i.e., those belonging to the same sublattice) is included, the system has nonzero Chern numbers.

Alba et al. suggest to use a formula for determining the Chern number of this model, where the input is the momentum-dependent spin $S (q)$ —a quantity that can, in principle, be measured. In cold atom systems, it is routine to measure the spin-dependent crystal momentum distributions, $〈 n_{↑, ↓} (q) 〉$ with time-of-flight techniques [8]. However, this technique alone only gives the $z$ -component of $S$ : $S_{z} (q)$ . NMR-like control of the atomic spin allows measurement of the two other components of $S (q)$ [Fig. 1(b)]. Simply approximating the expression for the Chern number for spin Hamiltonians with a discrete sum

over points $q$ spaced by $Δ q$ along $e_{x}$ and $e_{x}$ (the corresponding pixels in the experimental data) allows for a direct computation using experimentally measurable images of atoms without any further image processing. The Chern number can take the values $ν = - 1, 0, 1$ depending on the phase $ϕ$ of the laser that induces the tunneling between sites on the lattice.

Alba et al.’s seemingly simple observation leads to a more generalized conclusion: for a range of systems, the ability to measure both the crystal momentum distribution and to control single particle rotations in “spin space” make it possible to observe topological invariants. In contrast with conventional materials, this tunability is generally available in cold atom systems, which makes it possible to quickly identify those lattice configurations that are topological insulators.

Acknowledgments

G. J. acknowledges the support from the EU FP7 project NAMEQUAM, and I.B.S. acknowledges the NSF through the PFC at JQI, and the ARO with funds from both the Atomtronics MURI and the DARPA OLE Program.

References

M. Z. Hasan and C. L. Kane, Rev. Mod. Phys. 82, 3045 (2010)
E. Alba, X. Fernandez-Gonzalvo, J. Mur-Petit, J. K. Pachos, and J. J. Garcia-Ripoll, Phys. Rev. Lett. 107, 235301 (2011)
D. J. Thouless, M. Kohmoto, M. P. Nightingale, and M. den Nijs, Phys. Rev. Lett. 49, 405 (1982)
J. Dalibard, F. Gerbier, G. Juzeliūnas, and P. Öhberg, Rev. Mod. Phys. 83, 1523 (2011); arXiv:1008.5378(2011)
M. V. Berry, Proc. R. Soc. London A 392, 45 (1984)
Y. Aharonov and D. Bohm, Phys. Rev. 115, 485 (1959)
F. D. M. Haldane, Phys. Rev. Lett. 61, 1 (1988)
M. Anderlini, P. J. Lee, B. L. Brown, J. Sebby-Strabley, W. D. Phillips, and J. V. Porto, Nature 448, 452 (2007)

About the Authors

Gediminas Juzeliūnas is a principal researcher and a deputy director at the Institute of Theoretical Physics and Astronomy of Vilnius University, Lithuania. He is also professor of physics at Lithuanian University of Educational Sciences in Vilnius. Dr. Juzeliūnas completed his Ph.D. in 1986 in theoretical condensed matter physics at Vilnius University, studying optical properties of excitons in confined geometries. Subsequently he held a two-year postdoctoral appointment at the University of East Anglia, England, shifting his research area towards quantum optics. Dr. Juzeliūnas was a Humboldt Research Fellow at the University of Ulm, Germany (1997–1998), and a Fulbright Scholar at the University of Oregon in the US (2000–2001). Dr. Juzeliūnas received a National State Prize for Science of Lithuania in 2008 and a Vilnius University Rector’s award in 2010. His current research focuses on ultracold atomic gases, slow light, metamaterials, and graphene. This includes a pioneering theoretical work on light-induced gauge potential for ultracold atoms.

Ian Spielman in an experimentalist who received his Ph.D. in physics from the California Institute of Technology in 2004, studying quantum Hall bilayers. From there he moved to NIST in Gaithersburg, Maryland, for a two year NRC postdoc in the Laser Cooling and Trapping group, studying the physics of the superfluid-to-insulator transition in 2D atomic Bose gases. In 2006, he assumed his current position as a NIST physicist and a fellow of the newly founded Joint Quantum Institute (JQI). His research interests focus on using ultracold atomic systems to realize Hamiltonians familiar in condensed matter physics. This includes the pioneering work on creating artificial gauge fields for neutral atoms using laser atom interactions.