Fermion Pairing in Flatland

Mohit Randeria

Viewpoint

Fermion Pairing in Flatland

Mohit Randeria

Physics Department, Ohio State University, Columbus, OH 43210, USA

January 23, 2012• Physics 5, 10

Cold-atom experiments tread into the land of two-dimensional superconductivity.

Figure caption — **Figure 1:** Sommer *et al.* [1] use radio-frequency (rf) spectroscopy to determine the binding energy of paired lithium atoms in a cold gas. This cartoon shows a gas with two species of fermions, denoted by red and blue, which are analogous to the spin-up and spin-down electrons in a metal. The presence of an optical lattice potential (blue curve) tunes the dimensionality and forces the gas into stacks of quasi-two-dimensional layers. The interaction between the two types of fermions is tuned using a Feshbach resonance. Absorption of the rf photon (red wavy line) converts a fermion in the red state to a different internal state shown as green, and measures the pair binding energy.

Superconductivity and superfluidity in two dimensions (2D) has long been a subject of great interest. Materials with the highest known transition temperature $T_{c}$ , the cuprates, are quasi-2D systems with superconductivity originating in the 2D copper-oxide planes. A deeper understanding of strongly interacting 2D superconductors and their normal states could potentially give insights into the unsolved problem of high- $T_{c}$ superconductivity. Further, 2D is known to be the lower critical, or marginal, dimension both for pairing of fermions and for superfluidity. Thus 2D represents a borderline dimensionality, above and below which the system behaves qualitatively differently from a classical and a quantum perspective. Classically, thermal fluctuations of the order parameter destroy long-range order in 2D and lead to algebraic order at finite temperatures. In quantum mechanics, 2D is the marginal dimension for bound-state formation, which has important implications for the pairing of fermions that is essential for superfluidity. Finally, the effects of strong interactions in 2D Fermi systems present a formidable theoretical challenge.

A paper [1] appearing in Physical Review Letters reports experiments with ultracold Fermi gas of lithium- $6$ atoms that give new insight into how dimensionality and interactions affect the binding of fermions to form a superfluid. Ariel Sommer and his colleagues at the Massachusetts Institute of Technology, Cambridge, use two independent knobs: a magnetic field to tune interatomic interactions and an optical lattice to tune the dimensionality between 3D and 2D. They then use radio-frequency (rf) spectroscopy to probe pairing in the many-particle system and relate it to bound-state formation in the two-body problem in the 2D limit. Although theorists have predicted how this pairing energy evolves with interaction strength and dimensionality, until now there were no real systems on which to test these ideas.

In recent years there has been tremendous progress in controlling the interaction between atoms in ultracold gases with the Feshbach resonance technique, in which a magnetic field is used to tune the attractive $s$ -wave interaction between Fermi atoms in two different hyperfine states [2–4]. This is the analog of tuning the attraction between spin-up and spin-down electrons in a metal, which is, of course, impossible in solid-state materials. An important outcome of this progress has been the ability to explore the crossover from a condensate of Cooper pairs, described by Bardeen-Cooper-Schrieffer (BCS) theory, to a Bose-Einstein condensate (BEC) of tightly bound diatomic molecules in 3D ultracold gases. The most significant new insights have come from studies of the very strongly interacting states at resonance [2,3], which has scale-invariant properties [4] analogous to problems in nuclear physics and string theory.

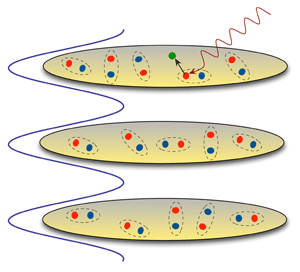
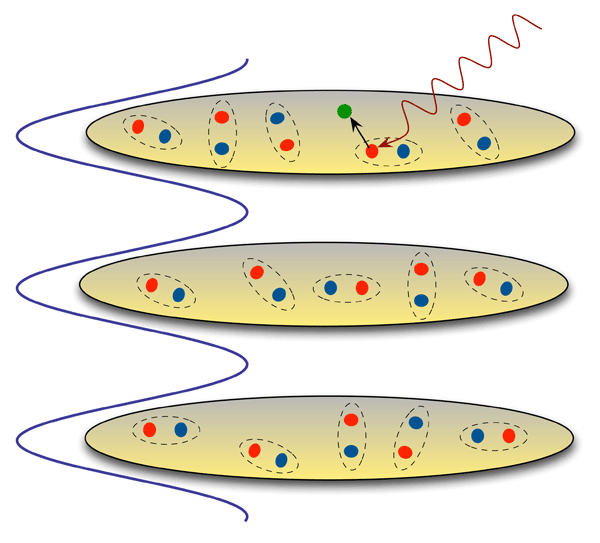
The experiment of Sommer et al. [1] builds on all of this progress with an optical lattice, which is a periodic potential that arises from interfering laser beams. By tuning the strength of this potential, $V_{0}$ , one can go from an anisotropic 3D system, for weak $V_{0}$ , to an essentially decoupled stack of 2D layers, in the limit of strong $V_{0}$ , which is shown schematically in Fig. 1.

The MIT team probes the pairing between atoms with rf spectroscopy [2], in which photons transfer Fermi atoms from one hyperfine state to another. The resulting absorption intensity as a function of photon energy has a characteristic asymmetric line shape with a threshold for bound-to-free transitions that contains information about the spectrum of fermionic excitations. The mean-field theory for a BCS-BEC crossover predicts that the rf threshold is given by [2] $ħ ω_{t h} = \sqrt{μ^{2} + Δ^{2}} - μ$ , where $μ$ is the chemical potential and $Δ$ the BCS gap parameter. It is important to emphasize that the rf threshold is not simply $Δ$ , in contrast to spectroscopic probes of electronic excitations in superconductors like tunneling. The reason is that rf photons excite Fermi atoms in all $k$ states and the threshold is determined by $k = 0$ fermions. Sommer et al. interpret the rf threshold $ħ ω_{t h}$ as the “pair binding energy” in the many-body system.

In 2D, the zero temperature mean-field equations for the $s$ -wave BCS-BEC crossover can be solved analytically for all interaction strengths, unlike the 3D case. The 2D results [5] for $Δ$ and $μ$ have very simple expressions involving only two parameters: the noninteracting Fermi energy and the binding energy $E_{b}$ of the two-body bound state. This leads to an rf threshold $ħ ω_{t h} = E_{b}$ . In other words, according to mean-field theory, the pair binding energy in the many-body system is exactly the same as that in the two-body problem.

This remarkable result might have been chalked up to the simplicity of mean-field theory, but Sommer et al. find that this prediction is borne out in their data. They show reasonable agreement with this theoretical result [5] over the entire range of interaction strengths from BCS to BEC regimes in the 2D limit. The experiment also looks at how the rf spectra evolve with dimensionality from 3D down to 2D. The threshold for formation of two-body bound states is gradually reduced as a function of increasing optical lattice intensity. The results are in agreement with theoretical calculations [6,7] of the two-particle problem in a 1D optical lattice (along $z$ , say, with free space propagation in the $x$ - $y$ plane).

The simultaneous tuning of both interactions and dimensionality is a very exciting development. These experiments are only the opening salvo in what is sure to become a major research area. It would be of great interest to experimentally probe the superfluid state and coherence across the layers in a quasi-2D system. Much of the physics lies beyond mean-field theory, and that will surely be explored in the future.

The 2D attractive Fermi gas has rich physics even in its normal, i.e., nonsuperfluid, state. Pair binding is enhanced in 2D and the superfluid $T_{c}$ is suppressed by classical phase fluctuations. Thus there is a large temperature regime in which pairing can occur without condensation, leading to characteristic pseudogap effects [8]. The first observation [9] of the pairing pseudogap in 2D fermions has just been reported using momentum-resolved rf spectroscopy [10].

Strongly interacting Fermi systems in 2D are among the least understood theoretically. On the one hand, exact solutions and other special techniques shed light on 1D many-body problems. On the other, fluctuation effects are, in general, less severe in 3D systems. But 2D systems are in the most challenging regime where few reliable theoretical results are available. This is precisely why experiments such as the one by Sommer et al. are so important for the development of the field.

Correction (24 January 2012): Paragraph 5 sentence 3, $ħ ω_{t h} = \sqrt{μ^{2} + Δ^{2}}$ changed to $ħ ω_{t h} = \sqrt{μ^{2} + Δ^{2}} - μ$

References

A. T. Sommer, L. W. Cheuk, M. J. H. Ku, W. S. Bakr, and M. W. Zwierlein, Phys. Rev. Lett. 108, 045302 (2012)
Ultracold Fermi Gases, Proceedings of the International School of Physics “Enrico Fermi,” Course CLXIV, edited by M. Inguscio, W. Ketterle, and C. Salomo (IOS Press, Amsterdam, 2008)[Amazon][WorldCat]; W. Ketterle and M. Zwierlein, Riv. Nuovo Cimento 31, 247 (2008)
S. Giorgini, L. P. Pitaevskii, and S. Stringari, Rev. Mod. Phys. 80, 1215 (2008)
M. Randeria, W. Zwerger, and M. Zwierlein, in BCS-BEC Crossover and the Unitary Fermi Gas, edited by W. Zwerger, Lecture Notes in Physics Vol. 836 (Springer, Berlin, 2012)[Amazon][WorldCat]
M. Randeria, J.-M. Duan, and L.-Y. Shieh, Phys. Rev. Lett. 62, 981 (1989); Phys. Rev. B 41, 327 (1990)
G. Orso, L. P. Pitaevskii, S. Stringari, and M. Wouters,  Phys. Rev. Lett. 95, 060402 (2005)
D. S. Petrov and G. V. Shlyapnikov, Phys. Rev. A 64, 012706 (2001)
M. Randeria, N. Trivedi, A. Moreo, and R. T. Scalettar, Phys. Rev. Lett. 69, 2001 (1992); N. Trivedi and M. Randeria, 75, 312 (1995); M. Randeria, in Models and Phenomelogy for Conventional and High-Temperature Superconductivity, Proceedings of the International School of Physics “Enrico Fermi,” Course CXXXVI, edited by G. Iadonisi, J. R. Schrieffer, and M. L. Chiafalo (IOS Press, Amsterdam, 1998)[Amazon][WorldCat]; arXiv:cond-mat/9710223v1
M. Feld, B. Frohlich, E. Vogt, M. Koschorreck, and M. Kohl, Nature 480, 75 (2011)
J. T. Stewart, J. P. Gaebler, and D. S. Jin, Nature 454, 744 (2008); J. P. Gaebler, J. T. Stewart, T. E. Drake, D. S. Jin, A. Perali, P. Pieri, and G. C. Strinati, Nature Phys. 6, 569 (2010)

About the Author

Mohit Randeria is a condensed-matter theorist on the faculty of the Ohio State University. His current research focuses on strong correlations, superconductivity, and magnetism in cold atoms and in quantum materials. He was educated at IIT-Delhi, Caltech, and Cornell. After post-doctoral research at Illinois he taught at Stony Brook University and was on the staff of Argonne National Labs and the Tata Institute of Fundamental Research. He is a Fellow of the American Physical Society and was awarded the 2002 ICTP Prize for Condensed Matter Physics.