The Longevity of Rankings

Guido Caldarelli

Viewpoint

The Longevity of Rankings

Guido Caldarelli

IMT Alti Studi Lucca, Piazza S. Ponziano 6, 55100 Lucca, Italy

September 17, 2012• Physics 5, 105

A phase transition controlled by noise determines how volatile rankings are.

Figure caption — **Figure 1:** Phase diagram of ranking stability in the $A$ – $B$ plane ( $A$ : fitness, $B$ : noise). For a given ranking system, $A$ is a vector of constants ( $A_{i}$ ) representing the “fitness” of all items of the ranked list, $B$ is a parameter measuring the ranking’s noise. Every real ranking system is represented by a line corresponding to the experimentally determined value of $B$ . In analogy to the classical phases of statistical mechanics, three phases are identified based on the stability of the top-ranked items: rank stable (solid), score stable (liquid), and unstable or volatile (gas). $B$ is the control parameter of the phase transition. The lower panel shows the rank evolution for the top-ranked items of a stable system (diseases diagnosis in Medicare) and a volatile one (page views in Wikipedia).

Whenever we use Google’s search engine, shop for bargains on Amazon, or evaluate a colleague through citation measures such as the $h$ -index, we are relying on rankings to bring order into large and complex datasets. We would be much better at making decisions if we could thoroughly understand the mechanisms that drive these rankings. Can we trust a ranking system to point out the items of highest quality? Can lousy items occasionally reach the top of a ranking? Will valuable ones always emerge? Certain rankings, like those measuring the number of times scientists are cited, show remarkable stability: it would take some effort to replace Einstein or Darwin as the most talked about scientists. Others, like bestseller lists, have a very volatile nature and fluctuate on a daily basis. Why such a different behavior? In Physical Review Letters, Nicholas Blumm at Northeastern University and the Dana-Farber Cancer Institute, both in Boston, Massachusetts, and colleagues report on a study of the volatility of several prominent ranking systems [1]. From their analysis, a unified theory of ranking stability emerges.

Researchers apply theories rooted in statistical mechanics to explain the properties of particularly important rankings. A ranking is typically described by distribution functions, relating the probability that an item is ranked at a certain position to key parameters of the system [2]. For example, the American linguist George Kingsley Zipf [3] observed that the usage rank of a word is, to a good approximation, inversely proportional to its frequency: the most frequent word will occur twice as often as the second most frequent word, three times as often as the third most frequent word, etc. This scaling applies to all languages and has been interpreted by Zipf [3] and more recent studies [4] in terms of a least-effort principle: minimization of the efforts of both hearer and speaker in a conversation leads to a Zipf-like distribution law, a hallmark of the efficient mechanisms by which human languages are generated. Similar scaling laws are observed in other rankings unrelated to language, such as the distribution of incomes described by the Italian economist Vilfredo Pareto [5], who noticed that a small proportion of a population owns a large part of the wealth. The coefficient of the Pareto’s power law is often taken as an indicator of a society’s inequalities. These examples illustrate how statistical analysis can reveal profound and sometimes hidden mechanisms that govern the system being ranked.

Blumm et al. go beyond the description of ranking distribution functions and focus instead on what determines their stability in time. The authors search for a common law regulating ranking dynamics by analyzing six prominent ranking systems: the use of individual words in published literature, the hourly page views in Wikipedia, the frequency of certain keywords used in Twitter, the daily market capitalization of companies, the number of diagnosis of a specific disease recorded by Medicare, and the number of article citations in the Physical Review corpus. Each ranking system is based on a different mechanism for assigning scores to different items of a list. The rank of a specific item is obtained by comparing its score to those of other items. Rank is thus a collective measure, depending both on an item’s score and on what happens to the rest of the ranked system.

The authors observe that the stability of an item’s rank depends on the fluctuations of the score around its mean value. An item ranked at a certain position ( $r$ ) is rank-stable if the score fluctuates less than the gap to the consecutively ranked items ( $r \pm 1$ ). To describe the score dynamics, Blumm et al. apply a universal stochastic equation (a Langevin equation) that can describe the evolution of systems under the simultaneous action of deterministic and stochastic forces. The authors assume that the deterministic and stochastic terms can be represented by power-law functions of the item’s score, weighted by a series of constants $A_{i}$ (for every item) and $B$ . The constant $A$ captures the “fitness” of each item, describing the aptitude to increase its score. For example, in social media, $A$ measures the ability to acquire new friends or followers, or in publishing, the capacity of an article to get new citations. $B$ , instead, models a Gaussian random noise that determines stochastic score fluctuations. For the six investigated rankings, the authors derive empirical values of $A$ and $B$ by fitting historical data.

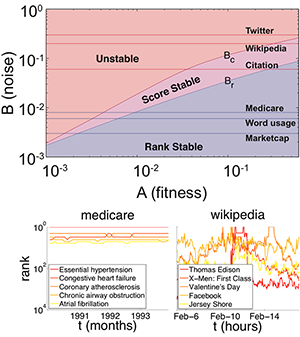
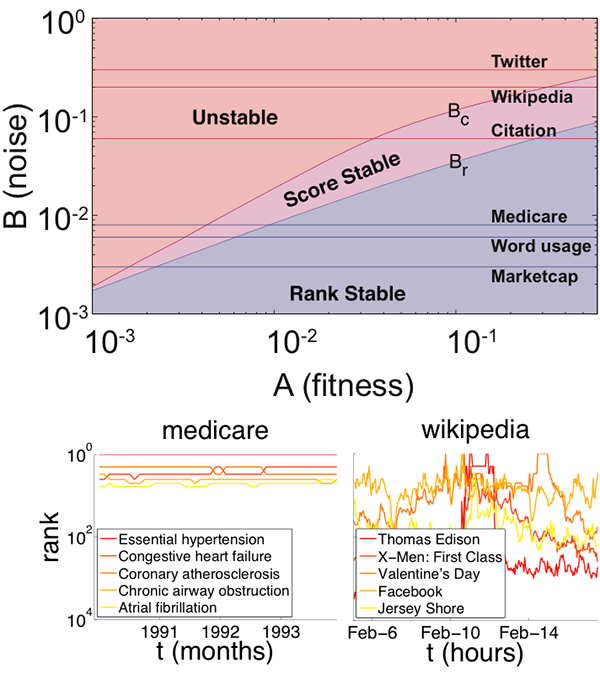
The interplay of these two weights determines the ranking within the system and, more importantly, its stability. The authors calculate the probability that a certain item with fitness $A$ has a certain score $x$ at a given time. Under the assumption that the system reaches a steady-state solution, they find that the most likely score depends on the relative value of fitness compared to other items’ fitness. The effect of the noise is to make the score fluctuate by a certain amount. The outcome depends critically on the value of the noise parameter $B$ . If the noise is lower than a certain critical value $B_{c}$ , the score remains localized around the original value. If the noise is larger than $B_{c}$ , the solution is no longer stable. Since the stability of the score does not necessarily imply rank stability, two distinct regimes can be found below $B_{c}$ . For noise between $B_{c}$ and a certain value $B_{r}$ , each item has a stable score, but the fluctuations are sufficient for items with comparable score to swap their rank. Below $B_{r}$ , both ranks and scores are stable. Blumm et al. demonstrate that the volatility of ranking can be captured by a phase diagram in the $A$ – $B$ plane (shown in Fig. 1), where ranking stability properties are plotted as a function of the two parameters $A$ and $B$ . Three phases are identified in analogy to the classical phases of statistical mechanics: ranking and score stable (solid), score-only stable (liquid), and volatile (gas). Transitions between different regimes of ranking volatility can be described as phase transitions in which the random noise ( $B$ ) is the control parameter.

The authors test the validity of this approach by considering the ranking dynamics for the top five items of the six investigated examples. In the $A$ – $B$ diagram, one can represent every real system with a line corresponding to the experimental value measured for $B$ (see Fig. 1). Medicare, word usage, and market cap are in the rank-stable regime, in which highly ranked items should display rank stability, a prediction that agrees with empirical results. Conversely, Twitter keywords usage and Wikipedia page views are in the unstable phase, with high volatility of both score and ranking. Finally, Physical Review citations fall in the score-stable, liquidlike phase: the scores fluctuate around a well-defined average, but this is not sufficient to maintain rank stability.

The work of Blumm et al. delivers a fresh contribution to the study of ranking in social and economic systems, formulating a universal, scale-invariant theory that captures the dynamics of a variety of rankings with wildly different volatility properties. Most of the differences can be attributed to a phase transition controlled by the stochastic noise strength. It is tempting to conclude that the ephemeral nature of modern social media like Twitter or Wikipedia explains the larger noise (hence volatility) compared to established rankings such as that of word usage in English literature. Further studies should explore in more detail the origin of noise in ranking. Another important direction for future research is the extension to correlated noise (in real-life systems, ranking fluctuations of different items may be mutually dependent).

It is reassuring to know that Darwin and Einstein will continue to top scientific rankings for the foreseeable future. However, as a statistical physicist, I am also intrigued by the fact that, in our ranking-obsessed world, a small fluctuation (or a bit of luck) may be all it takes to turn today’s also-ran into tomorrow’s number one.

References

N. Blumm, G. Ghoshal, Z. Forró, M. Schich, G. Bianconi, J-P. Bouchaud, and A-L. Barabási, ”Dynamics of Ranking Processes in Complex Systems,” Phys. Rev. Lett. 109, 128701 (2012)
M. Mitzenmacher, “A Brief History of Generative Models for Power Law and Lognormal Distributions,” Internet Math. 1, 226 (2004)
G. K. Zipf, Human Behavior and the Principle of Least Effort (Addison-Wesley, Cambridge, 1949)
R. Ferrer i Cancho and R. V. Solé, “Least effort and the origins of scaling in human language,” Proc. Natl. Acad. Sci. U.S.A. 100, 788 (2003)
V. Pareto, Cours d’Économie Politique (Librairie Droz, Geneva, 1896)

About the Author

Guido Caldarelli is Full Professor of Theoretical Physics at the IMT Alti Studi Lucca and a member of Complex System Institute, CNR, Italy, and of the London Institute for Mathematical Sciences. His research is focused on scale-free networks and self-similar phenomena, in particular on the application of network theory to the evaluation of systemic risk in financial and economic systems. He has worked at the University Sapienza in Rome, the University of Manchester, and the University of Cambridge. For more information about his research visit www.guidocaldarelli.com.