Spin-Sensitive Optics

Jean-Yves  Bigot

Viewpoint

Spin-Sensitive Optics

Institut de Physique et Chimie des Matériaux de Strasbourg, Université de Strasbourg–CNRS, 23 rue du Loess, BP 43, 67034 Strasbourg, France

January 23, 2012• Physics 5, 11

Advances in a magneto-optical technique will allow researchers to better understand how to control spins in a metal with short optical pulses.

Figure caption — **Figure 1:** A physicist, previously unable to distinguish between the charge and the spin of electrons, now probes the magnetization dynamics of a ferromagnetic nickel-iron grating with femtosecond pulses of $66 eV$ light, after illuminating the grating with a lower energy $1.6 eV$ pulse of light. Both pulses are polarized in the plane of incidence (the plane defined by the incoming and outgoing rays of light). (Inset) By varying the delay between the pump and the probe, it is possible to map out the characteristic time ( $τ_{th}$ ) in which the film demagnetizes.

Magnetic switching is the basis for numerous applications, such as the processing and storage of information on magnetic media. Magnets are typically polarized or switched by a magnetic field pulse, which exerts a torque on the spins to reverse them. But an attractive alternative is to use light pulses to modify the magnetic state of a material. Nowadays one can produce bursts of photons with a pulse width of less than one femtosecond ( $1 fs = 10^{- 15} s$ ) [1,2]—far faster than the time in which a magnetic field pulse can be generated. There is, however, still much to learn about the ways short light pulses interact with the magnetic properties of a material. The field of ultrafast spin dynamics [3]—or femtomagnetism [4,5]—that is developing around this topic has researchers working to tackle fundamental questions: How does an optical pulse flip the spins in a material? What are the best techniques for probing the process?

A paper appearing in Physical Review X from Chan La-O-Vorakiat, at the Joint Institute for Laboratory Astrophysics (JILA) and the University of Colorado, Boulder, and his colleagues addresses a long-standing puzzle in this field with a technique that opens up new ways to understand the magneto-optical properties of materials [6]. Previous experiments that measured the optical reflectivity of a ferromagnetic metal as a function of magnetic field (the magneto-optical response) have indicated that short pulses of visible or infrared light can demagnetize the metal; but it was later questioned if these experiments were able to separate the response of the spins from that of the electrons [7]. La-O-Vorakiat et al. have used extreme ultraviolet light to perform similar experiments, which gives them a much greater sensitivity to spin dynamics. They show that optical pulses do indeed demagnetize a ferromagnetic nickel film, restoring faith in straightforward and commonly used magneto-optical experiments. Their new method also enhances a reliable technique for probing the way spins respond to ultrafast optics, which will become increasingly useful in the development of high-speed, spin-based applications.

A short pulse of light shining on a metal interacts with both the electrons’ charge and spin. Electrons have two types of angular momentum: the orbital moment $L_{z}$ and the spin moment $S_{z}$ . (Here, $z$ is the direction perpendicular to the orbit.) At certain frequencies, the energy of an incident photon can be absorbed and excite the electrons to higher energy states with a different orbital momentum. The charges can, in turn, radiate photons: this is the origin of all elementary optical properties like refraction or absorption. What about the spins? They can be “flipped” directly ( $S_{z} = \pm ħ / 2$ ) with photons if one uses circularly polarized light, in which photons carry a quantum of angular momentum $\pm ħ$ (left- or right-circular polarization).

In many cases, the orbital $L_{z}$ and spin $S_{z}$ angular moments are not independent because of the spin-orbit interaction, so affecting the orbital momentum of an electron also affects its spin momentum. In addition to the spin-orbit interaction, the exchange interaction—a subtle quantum effect resulting from the symmetry and indistinguishability of the electrons—can separate up and down spins that occupy a band of energies in a metal into two bands. The effect of a light pulse on the exchange interaction is to reduce the energy splitting between these two bands, though this phenomenon that has not yet been explained theoretically.

These elementary concepts of spin-photon interaction show that both charges and spins are involved in a typical time-resolved optical experiment. Then how can one distinguish the contributions of the spins alone, independently of the charges? La-O-Vorakiat et al. succeeded by exciting ferromagnetic nickel films and film gratings with near-infrared optical pulses and probing the spins’ dynamics via specific transitions ( $M_{2, 3}$ edges) using extreme ultraviolet light. They also probed the magneto-optical response at the same infrared wavelength as the excitation pulse and observed the same time constant for the demagnetization process, which typically occurs within $\sim 100$ femtoseconds (fs) in transition metals. Their results agree with theoretical predictions that ultrafast magneto-optical measurements contain the information on the spins dynamics [8,9].

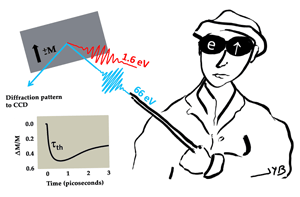
Chan La-O-Vorakiat et al.’s experiment was inspired by so-called “pump and probe” time-resolved magneto-optical setups. They first shine a $25$ fs pump pulse with photon energy $1.6$ electronvolts (eV) (a wavelength of $800$ nanometers) on a film of nickel metal. This pulse decreases the magnetization $M (t)$ of the metal, which they determine by measuring the intensity with which a second probe pulse is diffracted from the sample. This second pulse has an energy of $66 eV$ , which is nearly resonant with an atomic transition in nickel where $3 p$ core electrons are excited into empty $3 d$ valence levels. The spectrum of this so-called M-edge transition, and by extension the spectrum of the reflectivity performed near the M edges, depends on the magnetization of the sample because the magnetic moment associated with each nickel atom depends on how the valence $3 d$ levels are filled. To produce such a high-energy pulse using a tabletop laser, La-O-Vorakiat et al. had to use a high harmonic of light that was produced as a laser beam travelled down a capillary waveguide filled with a rare gas.

The group is able to probe the dynamics of the spins for different time delays between the two pulses. The information on the spins alone is obtained by measuring a change in the diffraction of the probe from a ferromagnetic grating, for a field polarization $p$ , parallel to the plane of incidence and with the magnetization perpendicular to this plane (Fig. 1). Each signal is measured with a magnetic field applied up and down; taking the difference between these two measurements insures the elimination of the charge contribution.

La-O-Vorakiat et al. measure the same demagnetization time—the characteristic time it takes for the sample to lose its magnetization—as the one measured with conventional time-resolved magneto-optics [3], which is important because it confirms this technique is looking at the same dynamics. In magneto-optics this demagnetization time is named the “thermalization time,” $τ_{th}$ , of the spins (inset, Fig. 1). $τ_{th}$ is the same for spins and charges when they are excited with low-intensity light, but starts to differ for higher intensities. The reason is that the interactions between “hot” spins in a ferromagnet that allow them to return to equilibrium experience large fluctuations when the spins are heated too close to the ferromagnet’s Curie temperature. The authors show that $τ_{th}$ is the same when probing the spins dynamics in the extreme ultraviolet spectral region or in the visible.

Optical magnetic resonance experiments are normally performed with x rays, but synchrotrons are typically needed to produce this high-energy radiation. La-O-Vokariat et al.’s work, which was performed with a tabletop laser, opens the way to making challenging new studies of magnetic materials within a laboratory environment. This is complementary to other experimental approaches using large-scale instruments like the synchrotron sources [10,11]. Indeed, experiments with ultrashort x-ray sources have recently revealed a powerful way for determining independently the dynamics of the spin $S_{z}$ and orbital $L_{z}$ moments with ferromagnetic [12] or antiferromagnetic order [13]. The study of ultrafast spin dynamics has entered a new era and it is very likely that the condensed-matter physics community will be strongly impacted by coming research in the field.

References

A. Rundquist, C. G. Durfee, Z. H. Chang, C. Herne, S. Backus, M. M. Murnane, and H. C. Kapteyn, Science 280, 1412 (1998)
M. Hentschel, R. Kienberger, Ch. Spielmann, G. A. Reider, N. Milosevic, T. Brabec, P. Corkum, U. Heinzmann, M. Drescher, and F. Krausz, Nature 414, 509 (2001)
E. Beaurepaire, J. C. Merle, A. Daunois, and J. Y. Bigot, Phys. Rev. Lett. 76, 4250 (1996)
G. Zhang, W. Hübner, E. Beaurepaire, J.-Y. Bigot, in Spin Dynamics In Confined Magnetic Structures I, edited by B. Hillebrands and K. Ounadjela, Topics in Applied Physics Vol. 83 (Springer, Berlin, 2002)[Amazon][WorldCat]
U. Bovensiepen, Nature Phys. 5, 461 (2009)
C. La-O-Vorakiat, E. Turgut, C. A. Teale, H. C. Kapteyn, M. M. Murnane, S. Mathias, M. Aeschlimann, C. M. Schneider, J. M. Shaw, H. T. Nembach, and T. J. Silva, Phys. Rev. X 2, 011005 (2012)
B. Koopmans, M. van Kampen, J. T. Kohlhepp, and W. J. M. de Jonge, Phys. Rev. Lett. 85, 844 (2000)
H. Vonesch and J.-Y. Bigot, arXiv:1201.0166v1 (2011)
J.-Y. Bigot, M. Vomir, and E. Beaurepaire, Nature Phys. 5, 461 (2009)
R. W. Schoenlein, S. Chattopadhyay, H. H. W. Chong, T. E. Glover, P. A. Heimann, C. V. Shank, A. A. Zholents, and M. S. Zolotorev, Science 287, 2237 (2000)
C. Stamm, T. Kachel, N. Pontius, R. Mitzner, T. Quast, K. Holldack, S. Khan, C. Lupulescu, E. F. Aziz, M. Wietstruk et al., Nature Mater. 6, 740 (2007)
C. Boeglin, E. Beaurepaire, V. Halté, V. López-Flores, C. Stamm, N. Pontius, H. A. Dürr, and J.-Y. Bigot, Nature 465, 458 (2010)
I. Radu, K. Vahaplar, C. Stamm, T. Kachel, N. Pontius, H. A. Dürr, T. A. Ostler, J. Barker, R. F. L. Evans, R. W. Chantrell et al., Nature 472, 205 (2011)

About the Author

Jean-Yves BIGOT is a Research Director at CNRS in France. After his Ph.D. from Université de Strasbourg, he spent two years at AT&T Bell Laboratories (Holmdel, NJ) and Lawrence Berkeley Laboratory (CA) in the groups of C. Shank and D. Chemla. He is an expert in the field of ultrafast processes in condensed-matter physics. His current research focuses on the study of dynamical processes in metallic and magnetic nanostructures, using femtosecond optical and magneto-optical spectroscopy. He received two prizes from the French Physical Society and was recently awarded the silver medal of CNRS for his outstanding contributions in the field of magnetization dynamics.

Ultrafast Demagnetization Measurements Using Extreme Ultraviolet Light: Comparison of Electronic and Magnetic Contributions

Chan La-O-Vorakiat, Emrah Turgut, Carson A. Teale, Henry C. Kapteyn, Margaret M. Murnane, Stefan Mathias, Martin Aeschlimann, Claus M. Schneider, Justin M. Shaw, Hans T. Nembach, and T. J. Silva

Phys. Rev. X 2, 011005 (2012)

Published January 23, 2012

Read PDF