Mind the (Quantum) Context
The contrast with classical expectations is one of the most intriguing features of quantum mechanics. It can be illustrated by playing a classic “guessing game” with quantum rules. In this case, the answer to one question will depend on the other questions being asked and the order chosen. This dependence on the context does not conform to our everyday experience, but we may have to live with it, as theorists have shown that we can’t just assume that there exists a hidden answer sheet that is unaffected by the choice of questions. However, designing a generic test of quantum contextuality in the lab has been difficult, so far. Writing in Physical Review Letters, Chong Zu of Tsinghua University in Beijing, China, and his colleagues have shown that context does matter in a three-level photon system generated by a simple but elegant linear-optics setup [1].
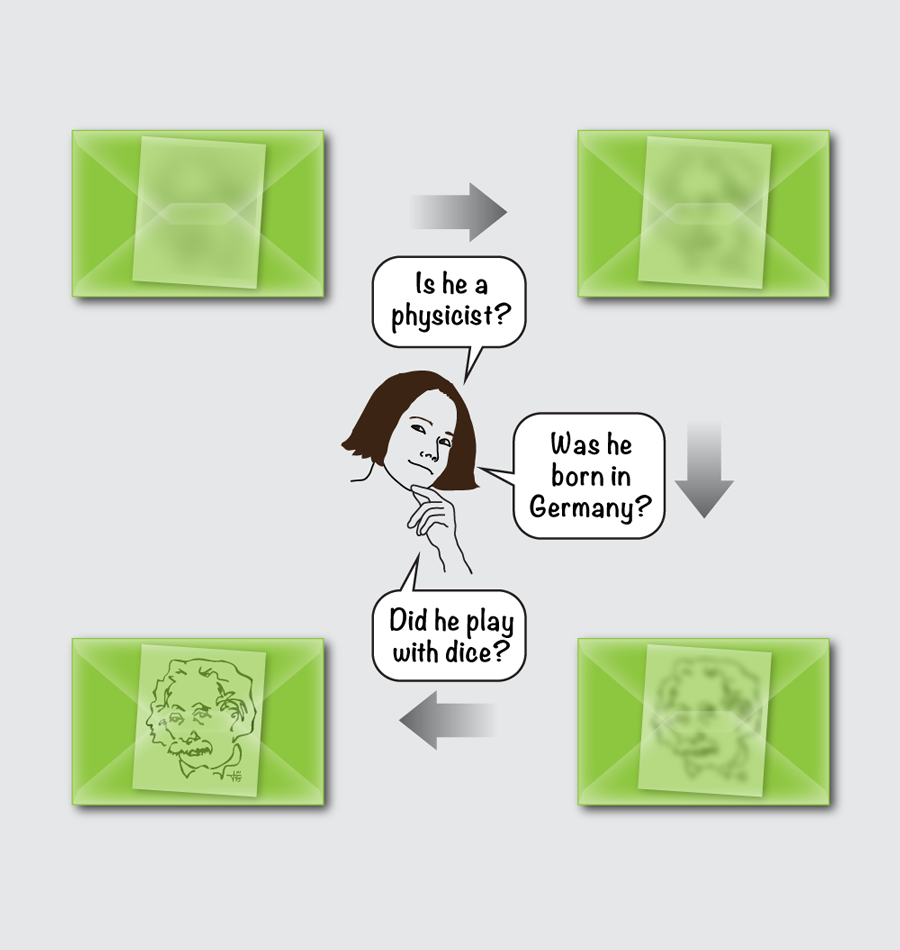
In the “Who am I” game, a closed envelope containing the name or picture of a celebrity is given to a player (say Alice). The celebrity’s identity is known to all the other players but not to Alice, who has a certain (agreed upon) number of questions to ask the others in order to find out the name in her envelope. Needless to say, the identity of the celebrity is there in the envelope, regardless of whether Alice is able to guess it or not. Moreover, it can’t magically change should Alice decide to ask if the hidden character “is a singer” before wondering whether or not he “was born in Duluth.” The name of the celebrity is a predetermined truth, independent of the questions that Alice decides to ask and the order she decides to ask them. It remains such even if the envelope is torn apart so that Alice will never see the answer. In a nutshell, it is noncontextual. This simple example shows that, in our daily experience, we consider the outcomes of our observations as simply the “revelation” of pre-existing elements of physical reality, which are there regardless of the specific context in which our observations are made.
Let us now transport the very same game to the bizarre (i.e., not familiar to our senses) quantum world. The questions asked by Alice to her companions are now embodied by measurements performed over the state of a system, whose outcomes are ruled by the probabilistic nature of the quantum formalism (see Fig. 1). Quantum observables do not have predefined values, and certain operators do not commute with each other. That means Alice now has to mind the order of her interrogations. In quantum “Who am I,” the name in the envelope could change if Alice asks about the celebrity’s occupation before asking where he or she was born. But the range of questions matters as well. The answer to “male or female?” may depend on whether or not Alice decides to ask about the celebrity’s hair color. In terms of an experiment, the outcome of an observation is critically dependent on the assignment of a set of mutually compatible (i.e., commuting) observables. In sum, quantum theory minds the context within which observations are performed. Even more strikingly, this contextuality is a general feature of all quantum states, not just a select subset.
Attempts to demystify the contextual character of the quantum framework have led to classically inspired models containing “hidden variables,” which are well-defined properties of a system that are inaccessible to the observer. According to these theories, the outcome of a measurement of an observable A is fully predetermined by a hidden variable λ, regardless of which other compatible observable is measured with A. Such local hidden variable models have been challenged by the work of Bell [2] and Kochen and Specker [3]. The latter developed a no-go theorem (widely known as the KS theorem), which proves the logical contradiction inherent in any attempt to interpret the outcome of a quantum measurement of A as resulting from a classical (i.e., commutative) joint probability distribution.
The original KS argument pinpoints the incompatibility between the classical structure of the hidden variable theories and quantum mechanics in a striking way, but it is quite experimentally unfriendly. The KS “guessing game” involves 117 different projectors onto complex vectors, which means an experimentalist would need to perform a very large number of observations on a quantum system. Subsequent work by Peres [4] and Mermin [5] greatly simplified the mathematical formulation of the KS theorem, condensing it into a mathematical inequality that forces a wedge between classical noncontextuality and (quantum) contextual theory. The outcomes of a specific set of observations are arranged together in a mathematical expression and compared to a bound set by classical hidden variable theories. If the observations are greater than this bound, then the inequality is said to be violated. The upshot of this violation is that hidden variables cannot be at work, and physicists have to content themselves with the nonintuitive consequences of quantum mechanics. The discriminating power of the KS-like inequality is similar to that of the well-known Bell’s inequality, which arose from Bell’s seminal work on nonlocality [6]. One distinct feature, however, of the KS-like argument is that quantum contextuality manifests itself regardless of the form of the quantum states under investigation. Such state-independent contextuality (SIC) means that all quantum states, not just specially prepared ones, violate our classical intuition. This is not the case for Bell-like inequalities, which are violated only by high-quality entangled states.
One requirement for most versions of the KS theorem is that the quantum system has at least three perfectly distinguishable configurations (or to say it another way, the Hilbert space must have dimension three or more). The creation of a single higher-dimensional system and the controlled implementation of different observations on that system are challenging tasks from the general experimental point of view. However, due to a strong interest from the community studying the foundations of quantum mechanics, many experimental groups have attempted in the last decade to demonstrate KS-like inequalities with various systems, such as neutrons, photons, and nuclear spins [7]. For instance, a very recent example [8] uses a composite system consisting of two trapped two-level ions, thus achieving the higher dimensionality required by SIC using two lower dimensional systems. Another group, using a linear optics experiment, was able to create a single indivisible quantum system for a KS-like demonstration, but the falsification of noncontextuality required a special initial state. [9].
This leaves room for the experimental demonstration of SIC along the lines of the original formulation of the no-go theorem, i.e., with the use of a single high-dimensional system and without the use of special initial states. Accepting this challenge, Zu and his colleagues designed their SIC test around a single photonic three-level system (a qutrit) [1]. The researchers encoded this qutrit by splitting a single photon with polarizing beam splitters, so that three possible paths (or levels) are available to the photon. For their observations, the team followed the recipe put forward by Yu and Oh and proven to be the most economical (in terms of the number of observables) by Cabello [10]. This set of “Who am I” questions consists of 13 compatible observables and 24 correlations between pairs of these observables, which Zu et al. measured using two cascaded Mach-Zehnder interferometers.
The experimental setup and techniques are simple, elegant, and quite well controlled. The research group had little room for error, since the discrepancy between the classical bound (or inequality) imposed by the Yu-Oh formulation of SIC and the value predicted by quantum mechanics is tiny (only about 4%). Despite unavoidable experimental uncertainties, the measurements by Zu et al. violated the classical bound (thus ruling out noncontextuality) by about 5 standard deviations, irrespective of the prepared system’s state. This statistically significant result sets a very good benchmark for experimental SIC with a single quantum system.
Have we thus seen the first unquestionable demonstration of genuinely state-independent contextuality of quantum mechanics? It is a reasonably close call, but not all the controversies that surround quantum foundation experiments on contextuality are ruled out by Zu and his colleagues. In particular, the effect of inefficiencies should not be overlooked. Photon losses induce no-click events at the detectors even when a single photon has been successfully heralded (and a qutrit state thus encoded). These missed detections affect the correlations entering the Yu-Oh inequalities. In order to accommodate this, the authors invoked the concept of fair sampling, which says that a long series of individual experimental runs should result in a satisfactory representative sample of the true joint probability distribution that we want to assess [9]. Therefore, Zu et al. discarded any no-click event from their data acquisition steps. As reasonable as this might sound, it embodies an extra assumption that was not included in the original KS argument nor in the formulation provided by Yu and Oh. Future experimental endeavors should strive to remove this extra ingredient, so that noncontextual theories have no experimental loopholes to hide behind.
PS: the celebrity that Alice had to guess in the classical “Who am I” round was Bob Dylan!
References
- C. Zu, Y-X. Wang, D-L. Deng, X-Y. Chang, K. Liu, P-Y. Hou, H-X. Yang, and L-M. Duan, “State-Independent Experimental Test of Quantum Contextuality in an Indivisible System,” Phys. Rev. Lett. 109, 150401 (2012)
- J. S. Bell, “On the Problem of Hidden Variables in Quantum Mechanics,” Rev. Mod. Phys. 38, 447 (1966)
- E. Specker, “Die Logik Nicht Gleichzeitig Entscheidbarer Aussagen,” (The Logic of Not Simultaneously Decidable Propositions) Dialectica 14, 239 (1960); S. Kochen, and E. P. Specker, “The Problem of Hidden Variables in Quantum Mechanics,” J. Math. Mech. 17, 59 (1967)
- A. Peres, “Incompatible Results of Quantum Measurements,” Phys. Lett. A 151, 107 (1990)
- N. D. Mermin, “Simple Unified Form for the Major No-Hidden-Variables Theorems,” Phys. Rev. Lett. 65, 3373 (1990)
- J. S. Bell, “On the Einstein Podolsky Rosen Paradox,” Physics 1, 195 (1964)
- M. Michler, H. Weinfurter, and M. Zukowski, “Experiments towards Falsification of Noncontextual Hidden Variable Theories,” Phys. Rev. Lett. 84, 5457 (2000); E. Amselem, M. Radmark, M. Bourennane, and A. Cabello, “State-Independent Quantum Contextuality with Single Photons,” 103, 160405 (2009); Y.-F. Huang et al., “Experimental Test of the Kochen-Specker Theorem with Single Photons,” 90, 250401 (2003); H. Bartosik et al., “Experimental Test of Quantum Contextuality in Neutron Interferometry,” 103, 040403 (2009); O. Moussa, C. A. Ryan, D. G. Cory, and R. Laflamme, “Testing Contextuality on Quantum Ensembles with One Clean Qubit,” 104, 160501 (2010)
- G. Kirchmair, F. Zähringer, R. Gerritsma, M. Kleinmann, O. Gühne, A. Cabello, R. Blatt, and C. F. Roos, “State-Independent Experimental Test of Quantum Contextuality,” Nature 460, 494 (2009)
- R. Lapkiewicz, P. Li, C. Schaeff, N. K. Langford, S. Ramelow, M. Wieśniak, and A. Zeilinger, “Experimental Non-Classicality of an Indivisible Quantum System,” Nature 474, 490 (2011)
- S. X. Yu, and C. H. Oh, “State-Independent Proof of Kochen-Specker Theorem with 13 Rays,” Phys. Rev. Lett. 108, 030402 (2012); arXiv:1112.5149