Entangled Microwaves Split Up
Entangled photons are the tools of choice for testing the foundations of quantum physics and demonstrating the teleportation of quantum states. They are also a resource in quantum information protocols. So far, most work has focused on entangled photons at optical frequencies. But for several decades, researchers have been developing a quantum information technology based on superconducting circuits, which have quantized excitations in the form of microwave photons. These circuits are attractive for generating, processing, and storing quantum information because they can be lithographically patterned on a small chip, allowing a good design to be replicated many times over. Now, in Physical Review Letters, Emmanuel Flurin and colleagues at École Normale Supérieure in Paris report they can generate, and then spatially separate, entangled microwave fields in a superconducting circuit [1], enabling quantum teleportation schemes that utilize microwave technology.
Entangled objects (such as two photons) are described by a common, nonseparable quantum-mechanical state. Measuring one object instantly changes the common state and therefore instantly affects the other object, even if it is far away—a phenomenon that seems to fly in the face of special relativity.
As a concept, entanglement got off to a rocky start. In 1935, Einstein, Podolsky, and Rosen (EPR) concluded that the “action at a distance” allowed by entanglement was so bizarre that quantum mechanics must be an incomplete theory [2]. They and others proposed the alternate theory of local hidden variables, which (loosely speaking) assumes entangled objects decide on a set of variables before they separate. A clear resolution didn’t emerge until 1964, when John Bell showed that the hidden variable theory set an upper bound on the degree of correlation between particles in an entangled state [3]. In contrast, quantum mechanics predicted that correlations for certain states exceeded, or “violated”, this upper bound. Violations of Bell’s inequality emerged again and again in quantum optics experiments, confirming that quantum entanglement was real. Still, the quest to find a loophole has continued to this day.
Even though it started as a suspicious property, by the nineties, entanglement was considered a technologically important resource for quantum cryptography and quantum computation. Other applications grew out of the fact that entangled photons can behave like an effective wave with half the photons’ wavelength, a feature that can be used to perform interferometry at sub-shot noise levels.
One advantage of using microwave superconducting circuits to test quantum physics and explore its applications is that the interaction between microwave photons is large compared to that found in optical photon technologies. These lithographically defined circuits are made from metals, like aluminum, which become superconducting when cooled to low temperatures. A central component within the circuit is the Josephson junction, a thin barrier that separates two superconducting stretches of metal. On either side of a Josephson junction, the Cooper-pair condensate is described by a macroscopic quantum mechanical wave function with an amplitude and a phase. The current through the junction is a sinusoidal function of the phase difference across the junction, which is in turn proportional to the time-integral of the voltage across the junction. As a result, unlike capacitors and inductors, Josephson junctions have a nonlinear response to currents, which makes it possible to engineer circuits that amplify or change the frequency of signals.
Even though they are macroscopic objects, superconducting circuits support quantized excitations of the electromagnetic field [4]. Researchers at NEC in Japan have used superconducting circuits to make a quantum bit [5] that could remain in a superposition of two charge states for a few nanoseconds. In the last few years, experimentalists at the University of California, Santa Barbara [6], have demonstrated a nine-element solid-state quantum processor that can factor the number 15, while researchers at IBM have observed coherent life times of a single superconducting qubit of up to 95 microseconds [7].
Building on this superconducting technology for quantum information processing, Flurin et al. take a first step towards engineering the circuits for quantum communication. The circuit they use for generating the entanglement is essentially a parametric amplifier, an ultralow-noise device that amplifies a quantum signal. In this case, they use it to amplify vacuum fluctuations (fluctuations that exist because the circuit is a quantum object) to create a so-called squeezed state.
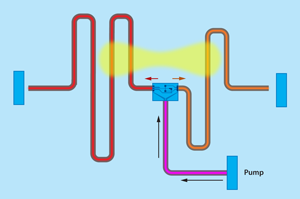
To do this, the team fabricated a chip (Fig. 1) that consists of two thin, serpentine aluminum channels that act as microwave resonators with different resonant frequencies ( fa≠fb). These resonators are coupled by a nonlinear circuit element consisting of several Josephson junctions. A third aluminum channel pumps coherent microwaves with frequency fp into the nonlinear crossing, which converts a pumped photon into a pair of photons, one in each resonator, whose frequencies fa and fb add up to the pump frequency. Since both photons originate from the same pump photon, they are correlated in a specific way, called two-mode squeezing [8], with the phase reference coming from the pump. The entanglement is then detected using a second device, similar to the one used to entangle the photons. With their device, Flurin et al. are able to produce pairs of entangled photons at a rate corresponding to six million entangled bits per second.
Two-mode squeezing of microwaves has been observed before [9], but it was at two different frequencies in a single transmission line. Flurin et al. are the first to create a two-mode squeezed microwave field where the two modes are spatially separated, thus showing entanglement in the original EPR sense. Taking a different approach, researchers in Germany, Spain, and Japan are now reporting on the arXiv that they can produce spatially separated entangled microwave photons [10] at a single frequency.
By demonstrating an efficient way to produce a flow of spatially separated entangled microwave photons, Flurin et al. have opened the door towards a new set of on-chip experiments in quantum information and measurement. One of the next steps will certainly be to demonstrate quantum teleportation with microwaves. Long term, researchers will look to interface microwave circuits, which are efficient at generating strongly interacting photons, with the fiber optic technology that works so well for sending light over long distances.
References
- E. Flurin, N. Roch, F. Mallet, M. H. Devoret, and B. Huard, “Generating Entangled Microwave Radiation Over Two Transmission Lines,” Phys. Rev. Lett. 109, 183901 (2012)
- A. Einstein, B. Podolsky, and N. Rosen, “Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?,” Phys. Rev. 47, 777 (1935)
- J. Bell, “On the Einstein Podolsky Rosen Paradox,” Physics 1, 195 (1964)
- M. Devoret et al., “Measurements of Macroscopic Quantum Tunneling out of the Zero-Voltage State of a Current-Biased Josephson Junction,” Phys. Rev. Lett. 55, 1908 (1985)
- Y. Nakamura, Yu. A. Pashkin, and J. S. Tsai, “Coherent Control of Macroscopic Quantum States in a Single-Cooper-Pair Box,” Nature 398, 786 (1999)
- E. Lucero et al., “Computing prime factors with a Josephson phase qubit quantum processor,” Nature Phys. 8, 719 (2012)
- C. Rigetti et al., “Superconducting Qubit in a Waveguide Cavity with a Coherence Time Approaching 0.1 ms,” Phys. Rev. B 86, 100506 (2012)
- C. M. Caves and B. L. Schumaker “New Formalism for Two-Photon Quantum Optics. I. Quadrature Phases and Squeezed States,” Phys. Rev. A 31, 3068 (1985)
- C. Eichler, D. Bozyigit, C. Lang, M. Baur, L. Steffen, J. M. Fink, S. Filipp, and A. Wallraff, “Observation of Two-Mode Squeezing in the Microwave Frequency Domain,” Phys. Rev. Lett. 107, 113601 (2011)
- E. P. Menzel et al., “Path Entanglement of Continuous-Variable Quantum Microwaves,” arXiv:1210.4413 (cond-mat.mes-hall)