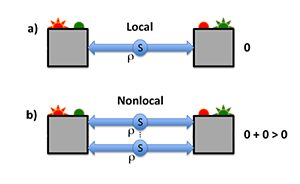
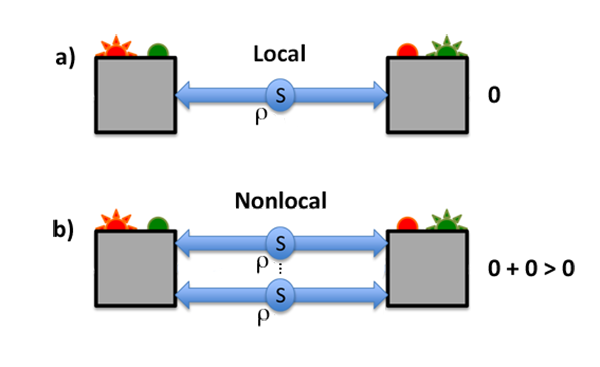
0 + 0 > 0
The idea that the whole can represent more than the sum of the parts is of fundamental importance in science, as illustrated in complexity theory: the emergent behavior of many complex systems cannot simply be derived from their individual components. In quantum mechanics, this phenomenon appears in a particularly subtle form: certain physical quantities, relevant to the description of quantum systems, are nonadditive. Loosely speaking, it is as if . Sometimes one can get something out of nothing! The origin of this effect lies in the fact that quantum mechanics allows for two (or more) systems to be measured jointly in a way that admits no analog in classical physics. Writing in Physical Review Letters, Carlos Palazuelos at the Institute of Mathematical Sciences in Spain presents a remarkable illustration of this phenomenon, showing that quantum nonlocality, arguably the most counterintuitive feature of quantum theory, is nonadditive [1]: the combination of a number of local quantum states can be nonlocal.
Locality means that an object is influenced directly only by its immediate surroundings and not by remotely located objects. The fact that quantum mechanics is at odds with this principle is not new. Back in the 1930s, Einstein, Podolsky, Rosen, and Schrödinger, first spotted this striking aspect of quantum theory as they pointed out the possibility of quantum entanglement. This led them to think that something was not quite right with quantum mechanics and that the theory had to be completed in a way that would restore locality. But this hope was to fall apart years later, when Bell proved that quantum mechanics is an inherently nonlocal theory that is simply incompatible with any physical theory in which the principle of locality holds [2]. Bell argued that in any local theory there are limits to how distant events are correlated. Mathematically, the correlation statistics must obey certain inequalities, now called Bell inequalities. Bell showed that two observers measuring states that are entangled would observe strong correlations between the results of their measurements: such correlations can be so strong that they violate Bell’s inequalities.
This phenomenon, called quantum nonlocality, has been repeatedly observed experimentally. For instance, in quantum optics experiments, it is now standard to create pairs of photons entangled in polarization. Then, each photon of the pair is sent (e.g., via an optical fiber) to a distant observer holding a polarization analyzer. The observed correlations between the results of both polarization measurements can lead to Bell-inequality violations, providing evidence that the physical world can be nonlocal [3]. Entanglement and nonlocality were first considered as two facets of the same physical effect, but they are now recognized as two different concepts, as research carried out in our group has demonstrated [4]. However, the relation between them is yet to be fully understood. While entanglement is absolutely necessary for quantum nonlocality, it is not always sufficient. Indeed, entangled, yet local, states exist: entangled quantum states can be prepared in such a way that their correlation statistics can never be distinguished from the classical case, as they do not violate any Bell’s inequality [5].
What happens when several entangled states are combined together? Is the nonlocality of the global (combined) state simply derived from the nonlocalities of each individual state? In other words, is nonlocality additive or do subtler effects occur? Beyond the purely conceptual interest, this question is relevant to quantum information science, where quantum nonlocality is a key resource for quantum information processing. For instance, secure quantum cryptography schemes rely on nonlocality: the strong quantum correlation of a sequence of bits exchanged by two communicating parties can be used to generate a secret cryptographic key known only to them [6]. Therefore, if one achieves nonlocality by combining two states that are local (hence useless from a quantum cryptography perspective), this may open new perspectives.
In recent years, a number of researchers attempted to challenge the additivity of quantum nonlocality [7]. In this work, Palazuelos gives the ultimate proof that quantum nonlocality is indeed nonadditive. He demonstrates that entangled, local states exist that become nonlocal when several copies of them are combined. The author starts with a specific quantum state ( ) that is entangled but local. Next, he shows how to construct a nonlocal state by combining several copies of ( ⊗ ⊗ … ⊗ , times). [In the formalism of quantum mechanics, the combination of quantum states is indicated by a tensor product (⊗)]. If a sufficiently large number of copies is combined, the resulting state is shown to violate a Bell inequality, i.e., it is nonlocal (see Fig. 1). This abstract procedure can be illustrated by the following example. Consider a source emitting pairs of photons in a polarization-entangled state , detected by two observers. This state is designed to be local: the correlations measured by the observers are not strong enough to reveal any nonlocality. However, if the source emits pairs, all in the same state , and each observer can perform simultaneous measurements on all the photons that he receives, then a Bell inequality violation can be achieved. Hence the global state, consisting of copies of , is nonlocal.
Importantly, this effect is only possible because quantum mechanics allows for “entangled measurements,” which have no analog in classical physics. Two (or more) quantum systems can be measured jointly in an entangled basis (i.e., a basis in which the eigenstates are entangled). Loosely speaking, one can think of these joint measurements as extracting information about the global state of the system without revealing individual properties. For instance, this could be done in an entangled measurement of the polarization of two photons, telling us whether the photons have the same polarization or not, without revealing the polarization of each individual photon. Such measurements, which are central in quantum teleportation and computation, are also key to Palazuelos’ results.
Another key ingredient in Palazuelos’ demonstration is a class of violations of Bell’s inequalities called “unbounded,” which were discovered by himself and coauthors [8]. They proved mathematically that certain quantum states can be prepared for which correlations are dramatically stronger than correlations achievable classically. In fact, by proper choice of states and measurements, this quantum vs classical separation can become arbitrarily large, hence the term “unbounded.” Reference [8] posed a purely mathematical proof of existence, but Buhrman and colleagues [9] then reported the first explicit example of a quantum state , enabling such unbounded violations of Bell’s inequalities. Armed with this knowledge, Palazuelos took the next step by demonstrating that the quantum state found by Buhrman et al. admits, in fact, a very simple structure: it can be decomposed as = ⊗ ⊗ … ⊗ ( times), where is an entangled state that is local. For sufficiently large , the Bell inequality can be violated. This effect is called the superactivation of quantum nonlocality.
The work of Palazuelos represents considerable progress in the field, as it resolves one of the longstanding questions in quantum nonlocality. At the same time, it raises many new ones. An important question is indeed whether superactivation of nonlocality is possible for any entangled state that admits a local representation. Progress in this direction was already reported: building upon Palazuelos’ work, it was recently shown by researchers [10], including one of us (N.B.), that all entangled states that are useful for teleportation can be superactivated, thus establishing a firm link between teleportation and nonlocality—two concepts previously believed to be unrelated [11]. In the longer term, these ideas may help us understand how entanglement and nonlocality relate to each other, a central question in the foundations of quantum mechanics that may also have important implications for quantum information science.
References
- C. Palazuelos, “Superactivation of Quantum Nonlocality,” Phys. Rev. Lett. 109, 190401 (2012)
- J. S. Bell, “On the Einstein Podolsky Rosen Paradox,” Physics 1, 195 (1964)
- A. Aspect, “Bell’s Inequality Test: More Ideal Than Ever,” Nature 398, 189 (1999)
- N. Brunner, N. Gisin, and V. Scarani, “Entanglement and Nonlocality are Different Resources,” New J. Phys. 7, 88 (2005)
- R. F. Werner, “Quantum States with Einstein-Podolsky-Rosen Correlations Admitting a Hidden-Variable Model,” Phys. Rev. A 40, 4277 (1989); M. L. Almeida, S. Pironio, J. Barrett, G. Toth, and A. Acin, “Noise Robustness of the Nonlocality of Entangled Quantum States,” Phys. Rev. Lett. 99, 040403 (2007)
- A. K. Ekert, ”Quantum Cryptography Based on Bell’s Theorem,” Phys. Rev. Lett. 67, 661 (1991); J. Barrett, L. Hardy, and A. Kent, “No Signaling and Quantum Key Distribution,” 95, 010503 (2005); A. Acin, N. Gisin, and L. Masanes, ”From Bell’s Theorem to Secure Quantum Key Distribution,” Phys. Rev. Lett. 97, 120405 (2006)
- L. Masanes, Y.-C. Liang, and A. C. Doherty, “All Bipartite Entangled States Display Some Hidden Nonlocality,” Phys. Rev. Lett. 100, 090403 (2008); D. Cavalcanti, M. L. Almeida, V. Scarani, and A. Acin, “Quantum Networks Reveal Quantum Nonlocality,” Nat. Comm. 2, 184 (2011); A. Sen(De), U. Sen, Č. Brukner, V. Bužek, and M. Żukowski, “Entanglement Swapping of noisy states: A kind of superadditivity in nonclassicality,” Phys. Rev. A 72, 042310 (2005)
- M. Junge, C. Palazuelos, D. P´erez-Garcia, I. Villanueva, and M. M. Wolf, “Operator Space Theory: A Natural Framework for Bell Inequalities,” Phys. Rev. Lett. 104, 170405 (2010)
- H. Buhrman, O. Regev, G. Scarpa, , and R. de Wolf, “Near-Optimal and Explicit Bell Inequality Violations,” IEEE Conference on Computational Complexity 2011, 157 (2011)
- D. Cavalcanti, A. Acin, N. Brunner, and T. Vertesi, “All Quantum States Useful for Teleportation are Nonlocal Resources,” arXiv:1207.5485
- S. Popescu, “Bell’s Inequalities Versus Teleportation: What is Nonlocality?” Phys. Rev. Lett. 72, 797 (1994)