Optical Atomic Clocks Could Redefine Unit of Time

Fritz Riehle

Viewpoint

Optical Atomic Clocks Could Redefine Unit of Time

Fritz Riehle

Physikalisch-Technische Bundesanstalt (PTB), Bundesallee 100, 38116 Braunschweig, Germany

November 12, 2012• Physics 5, 126

Optical atomic clocks now outperform the best microwave cesium atomic clocks in terms of precision.

Figure caption — **Figure 1:** Standards keep going up for atomic clocks. A timeline of the fractional uncertainty of the best cesium atomic clocks (blue squares) and the best optical frequency standards (red and green circles.) The red circles correspond to uncertainties determined by referencing the frequency to the cesium clock; the green circles correspond to estimated uncertainties. The white data point represents the new result of Madej *et al.*.

“Never measure anything but frequency!” was the advice [1] of the late Arthur Schawlow, the 1981 Nobel Prize winner in physics. Frequency is, in fact, the physical quantity that can be measured with by far the greatest accuracy. This is because it can be referenced to a highly accurate standard: the cesium atomic clock, in which a second is defined as $9 192 631 770$ periods of the microwave radiation emitted by a cesium- $133$ atom transitioning between two nuclear spin (hyperfine) states [2]. Now, in Physical Review Letters, Alan Madej and colleagues at the National Research Council in Canada report they have greatly increased the accuracy with which another atomic frequency standard, the optical transition in an isolated strontium ion, can be measured. Furthermore, the precision of their frequency measurement now supersedes that of the existing cesium standard, which could lead to the adoption of a new frequency standard for defining the second as the basic unit of time [3].

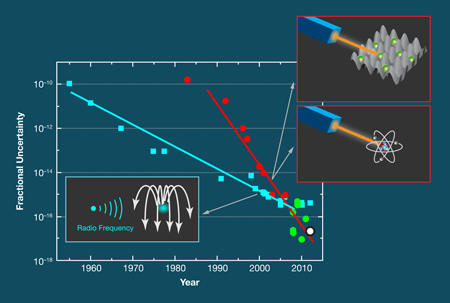
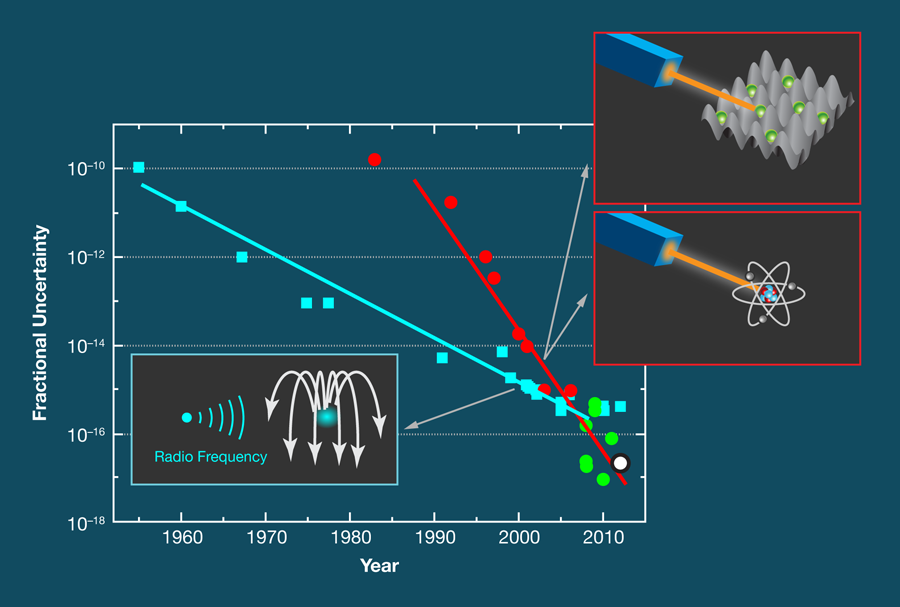
Frequency measurements are accurate (and unambiguous) because they essentially involve counting the number of times a periodic signal crosses zero. Today’s best cesium atomic clocks, which define the International System of Units (SI) standard of the second, are accurate to a few parts in $10^{16}$ (see, e.g., Ref. [4] and references therein). Since 1960, the accuracy of atomic clocks has increased by about one order of magnitude per decade (see Fig. 1).

Optical frequency standards have, however, been catching up in terms of accuracy. The measurement of frequency in an optical frequency standard is similar to that in atomic clocks with the exception that, instead of a microwave oscillator, an ultrastable laser probes a narrow-band optical transition in an ensemble of (neutral) atoms or a single ion. Breakthroughs in optical frequency measurement [5], laser stabilization [6], and laser manipulation of quantum absorbers have greatly increased the accuracy of optical atomic frequency standards. And, optical clocks outperform the best cesium clocks with respect to relative frequency stability because they work at roughly $100 000$ times the frequency. Here, however, one has to be cautious. In the same way that you can’t time an event with better accuracy than the stopwatch you’re using, no clock can be more accurate than the best cesium clocks with which they are compared. Nevertheless, optical frequency standards can be shown to reproduce the unperturbed line center of an atomic transition much better than cesium atomic clocks.

The optical frequency standard that Madej and co-workers have developed is based on a laser-cooled, single $^{88} {Sr}^{+}$ ion, which is held in the electrodynamic field of a radio-frequency trap. In this case, the “standard” is the frequency to which they must tune a laser so that it matches the ion’s $5 s$ $^{2} S_{1 / 2}$ − $4 d$ $^{2} D_{5 / 2}$ transition—a transition with a natural line quality factor of about $10^{15}$ . (For comparison, this quality factor is twelve, eleven, and five orders of magnitude higher than that of a tuning fork, a quartz crystal in a wristwatch, and the transition in a primary cesium fountain clock, respectively.) But Madej et al. also have to have an accurate “ruler” with which to determine their laser frequency. Over the course of several months, they repeatedly measured the frequency of the tuned laser by referencing it to one of the precisely spaced optical lines of a “frequency comb”. The comb is produced by the femtosecond pulses of a laser, which itself is referenced to a hydrogen maser [4]. Completing the chain of frequency references, the maser is compared to the international SI second via time-coded signals from the satellites of the Global Positioning System. These signals are regularly monitored in a “common view” mode by researchers at time laboratories worldwide, who compare the signals with their own primary clocks.

From measurements made over a period of about $100$ days, Madej et al. have been able to derive a value for the frequency of the $^{88} {Sr}^{+}$ optical transition of $444 779 0444 095 485.5$ hertz with a fractional uncertainty of $2$ x $10^{- 15}$ . Here, the uncertainty is mainly limited by the time reference they used. The authors showed in an elaborate set of investigations that the fractional uncertainty of the strontium frequency standard contributed only $2$ x $10^{- 17}$ , which is an order of magnitude lower than the fractional uncertainty of the best cesium clocks.

There are other optical frequency standards based on single ions that come up with similarly low uncertainties, e.g. [7,8]. The most precise standard uses ${Al}^{+}$ ions and is based on a quantum logic scheme developed by this year’s Nobel Prize winner Dave Wineland [8]. Optical frequency standards based on a large number of neutral $Sr$ atoms are envisaged to lead to similarly low uncertainties [9], which means that one can now reproduce optical frequencies that are much more precise than they are accurate.

Consequently, in the long run, one can expect that optical frequency standards will replace the cesium hyperfine transition in the definition of the second in the International System of Units. In order to investigate the best candidates for a redefinition of the second, the International Committee of Weights and Measures has selected a handful of suitable standards to act as so-called a “secondary representations” of the second. The $^{88} {Sr}^{+}$ clock is among them [10]: as a result of the work in Madej’s group, the Consultative Committee for Time and Frequency has already suggested that the uncertainty of this standard as a secondary representation should be reduced.

As optical atomic frequency standards and clocks progress, they will have considerable impact on various fields in science and technology. More stable and accurate time scales will directly influence global navigation satellite systems, with potentially direct impact on deep space navigation. Better clocks boost new ways of testing fundamental theories, like the special and general theory of relativity and quantum electrodynamics, as well as the constancy of fundamental constants. Today, the theories of general relativity and quantum mechanics both work extremely well in their specific field of application, but they are not mutually compatible. Most of the attempts to find an overarching theory containing both predict a variation of the fundamental constants. The comparison of different optical clocks presently sets the most stringent limits for laboratory experiments on such a temporal variation [11].

The availability of better clocks will also lead to new fields of research and applications like relativistic geodesy, in which the Earth’s gravitational potential can be determined by the local change of a high-accuracy clock when compared with a remote reference clock. The availability of a frequency standard with $10^{- 18}$ fractional uncertainty—still beyond the accuracy of existing clocks—would allow one to measure Earth’s geoid (the shape of its gravitational potential) at a level of $1$ cm, with the proper application and calculation of general relativistic corrections for the clocks and their comparisons. Astronomy and space applications will benefit from better clocks allowing ultraprecise tracking of space crafts, from better reference systems, and maybe later, even from a master clock in space.

References

P. Schewe and B. Stein, “Berkeley Symposium Celebrates Laser Pioneer,” Phys. News Update, http://www.aip.org/pnu/2005/749.html
SI base units, http://www.bipm.org/en/si/base_units/
A. A. Madej, P. Dubé, Z. Zhou, J. E. Bernard, and M. Gertsvolf, “88Sr+ 445-THz Single-Ion Reference at the 10{-17} Level via Control and Cancellation of Systematic Uncertainties and Its Measurement against the SI Second,” Phys. Rev. Lett. 109, 203002 (2012)
S. Weyers, V. Gerginov, N. Nemitz, R. Li, and K. Gibble, “Distributed Cavity Phase Frequency Shifts of the Caesium Fountain PTB-CSF2 ,” Metrologia 49, 82 (2012)
Th. Udem, R. Holzwarth, and T. W. Hänsch, “Optical Frequency Metrology,” Nature 416, 223 (2002)
T. Kessler, C. Hagemann, C. Grebing, T. Legero, U. Sterr, F. Riehle, M. J. Martin, L. Chen, and J. Ye, “A Sub-40-mHz-Linewidth Laser Based on a Silicon Single-Crystal Optical Cavity,” Nature Photon. 6, 687 (2012)
N. Huntemann, M. Okhapkin, B. Lipphardt, S. Weyers, C. Tamm, and E. Peik, “High-Accuracy Optical Clock Based on the Octupole Transition in 171Yb+,” Phys. Rev. Lett. 108, 090801 (2011)
C. W. Chou, D. B. Hume, J. C. J. Koelemeij, D. J. Wineland, and T. Rosenband, “Frequency Comparison of Two High-Accuracy Al+ Optical Clocks,” Phys. Rev. Lett. 104, 070802 (2010)
T. L. Nicholson, M. J. Martin, J. R. Williams, B. J. Bloom, M. Bishof, M. D. Swallows, S. L. Campbell, and J. Ye, “Comparison of Two Independent Sr Optical Clocks with 1x10 ^-17 Stability at 10^3 s,” arXiv:1210.0064v1 (physics.atom-ph); Phys. Rev. Lett. (to be published)
Recommended values of standard frequencies, http://www.bipm.org/en/publications/mep.html
T. Rosenband et al., “Frequency Ratio of Al+ and Hg+ Single-Ion Optical Clocks; Metrology at the 17th Decimal Place,” Science 319, 1808 (2008)

About the Author

Fritz Riehle received the degrees of Dipl. Phys., Dr. rer. nat., and Dr. habil. rer. nat. from the Technical University of Karlsruhe, Karlsruhe, Germany, in 1975, 1977, and 1981, respectively. His research interests include the realization of optical length and frequency standards, high-resolution spectroscopy, laser cooling, and atom interferometry. Since 2000, he has been in charge of the Optics Division of the Physikalisch-Technische Bundesanstalt (PTB) in Braunschweig. He is an Honorary Professor of the Leibniz University Hannover, where he is engaged in the Centre for Quantum Engineering and Space-Time Research.