Modeling Quantum Field Theory

Jeff Steinhauer

Viewpoint

Modeling Quantum Field Theory

Department of Physics, Technion–Israel Institute of Technology, Technion City, Haifa 32000, Israel

November 26, 2012• Physics 5, 131

An analog of the dynamical Casimir effect has been achieved, where phonons replace photons and thermal fluctuations replace vacuum fluctuations.

Figure caption — **Figure 1:** A resonator for the dynamical Casimir effect. The initial length of the resonator is shown in the upper illustration. The sine wave represents one of the modes of the resonator, initially populated by vacuum fluctuations. The length of the resonator is suddenly changed (lower illustration). The wavelength and frequency of the sinusoidal mode changes rapidly. The change is nonadiabatic, so the vacuum fluctuations are amplified, creating real photons.

Empty space is constantly fluctuating with virtual photons, which come into existence and vanish almost immediately. While these virtual photons are all around us, they cannot be observed directly. However, in a special kind of environment with spatial or temporal inhomogeneity, virtual photons can become real, observable photons by means of a variety of effects. Unfortunately, creating such environments can be exceedingly difficult.

The challenge can be made easier by using a condensed-matter analog to the vacuum and its photon modes [1]. In Physical Review Letters, Jean-Christophe Jaskula and colleagues at the University of Paris-Sud, France, report that they have created such an analog for the dynamical Casimir effect, in which a rapidly changing resonator (Fig. 1) produces real particles [2]. In addition to being a condensed-matter system, their observation is an analogy in another way: The real particles they observe originate from thermal fluctuations rather than quantum fluctuations of the vacuum. Their work opens the door for the observation of the quantum vacuum version, in their condensed-matter analog system.

The phenomenon studied by Jaskula and co-workers was studied previously by Engels and colleagues [3], but the interpretation was strictly classical. The real particles created were referred to as Faraday waves, oscillatory patterns that appear at half of the driving frequency. Now, Jaskula and colleagues [2] show that the waves have pair correlations in momentum space, thus making the connection with quantum-mechanical pair production and the dynamical Casimir effect.

The real dynamical Casimir effect (not the analog effect) was observed in Ref. [4]. However, such observations of the production of real particles are scarce due to the experimental challenges. For each effect, including the dynamical Casimir effect, these challenges are formidable.

In the Schwinger effect, for example, a homogeneous electric field can pull apart pairs of oppositely charged virtual particles [5]. The electric field should be strong enough to give an acceleration of $m c^{3} / ħ$ , where $m$ is the mass of the particles. Thus, to produce an electron-positron pair, an electric field of $10^{18} V / m$ is required, giving an acceleration of $10^{29} m / s^{2}$ . To put this in perspective, if this acceleration were maintained in the laboratory reference frame, the electron would reach the speed of light from rest within a distance of $10^{- 13} m$ .

The event horizon of a black hole can also convert pairs of virtual particles (such as photons) to real particles, which are referred to as Hawking radiation [6]. One of the members of the pair has negative energy, and the other positive. Within the event horizon, the negative energy photon of the virtual pair can exist indefinitely, allowing the positive energy photon to exist also. This real photon travels away from the black hole as Hawking radiation. Unfortunately, the radiation is too weak to observe with current technology. Creating or finding a very small black hole would help the effort.

On the other hand, virtual photons can be detected by accelerating the detector of the photons (the Unruh effect) [7]. In the reference frame of the detector, the virtual photons of the vacuum will appear to be a thermal distribution of real photons. In other words, the virtual photons are Doppler shifted into reality. A detector accelerating at $10^{20} m / s^{2}$ would measure a radiation temperature of only $1 K$ .

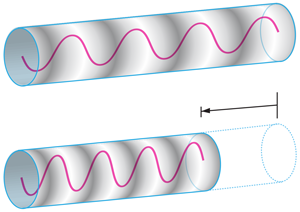
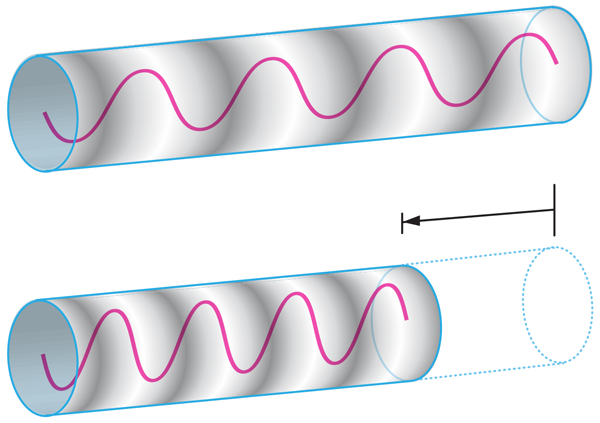
Another way to detect the virtual photons is to rapidly change the nature of the vacuum. In the dynamical Casimir effect, a resonator has a discrete spectrum of eigenmodes [8]. These modes are populated with the virtual vacuum fluctuations. One such mode is illustrated in Fig. 1. Suddenly, the length of the resonator is changed very rapidly, at a speed which is a significant fraction of the speed of light (the experimental challenge). The change is too fast to be adiabatic, so the population of the virtual vacuum fluctuations is amplified. The extra population consists of real, observable particles.

As we can see, it is a challenge to convert virtual particles into real, observable particles. In all cases, the experimental parameters which must be achieved are formidable. But what if we could replace the speed of light with the speed of sound? In a Bose-Einstein condensate, phonons could play the role of the photons, and the condensate itself could play the role of the quantum vacuum. This is the idea of the condensed-matter analog [1]. Following the suggestion of Carusotto et al. [9], Jaskula and colleagues used a cigar-shaped Bose-Einstein condensate as a resonator for the analog of the dynamical Casimir effect [2].

In the experiment of Jaskula et al., the Bose-Einstein condensate was confined by focused laser light. The atoms forming the condensate were attracted to the bright light like insects to a lamp. In one experiment, the authors suddenly increased the laser intensity by a factor of $2$ , which caused an abrupt increase in the speed of sound in the condensate, and a sudden decrease in the resonator length, as indicated in Fig. 1. Each thermally populated mode was unable to follow the sudden change adiabatically. This resulted in the production of pairs of phonons with equal and opposite momenta, and a wide distribution of momenta was observed. In another experiment, the laser intensity was modulated sinusoidally, with a variation of about $10 %$ . This resulted in pairs of phonons with frequencies equal to half of the modulation frequency, thus demonstrating the connection between the dynamical Casimir effect and parametric down-conversion of nonlinear optics [9].

The ongoing study of the dynamical Casimir effect is part of our effort to convince ourselves that empty space is truly filled with virtual particles. If they are really there, then we want to see them in the real vacuum, as well as in a Bose-Einstein condensate analog of vacuum.

References

W. G. Unruh, “Experimental Black-Hole Evaporation?” Phys. Rev. Lett. 46, 1351 (1981)
J-C. Jaskula, G. B. Partridge, M. Bonneau, R. Lopes, J. Ruaudel, D. Boiron, and C. I. Westbrook, “Acoustic Analog to the Dynamical Casimir Effect in a Bose-Einstein Condensate,” Phys. Rev. Lett. 109, 220401 (2012)
P. Engels, C. Atherton, and M. A. Hoefer, “Observation of Faraday Waves in a Bose-Einstein Condensate,” Phys. Rev. Lett. 98, 095301 (2007)
C. M. Wilson, G. Johansson, A. Pourkabirian, M. Simoen, J. R. Johansson, T. Duty, F. Nori, and P. Delsing, “Observation of the Dynamical Casimir Effect in a Superconducting Circuit,” Nature 479, 376 (2011)
R. Brout, S. Massar, R. Parentani, and Ph. Spindel, “A Primer for Black Hole Quantum Physics,” Phys. Rep. 260, 329 (1995)
S. W. Hawking, “Black Hole Explosions?” Nature 248, 30 (1974)
W. G. Unruh, “Notes on Black-Hole evaporation,” Phys. Rev. D 14, 870 (1976)
V. V. Dodonov, “Current Status of the Dynamical Casimir Effect,” Phys. Scr. 82, 038105 (2010)
I. Carusotto, R. Balbinot, A. Fabbri, and A. Recati, “Density Correlations and Analog Dynamical Casimir Emission of Bogoliubov Phonons in Modulated Atomic Bose-Einstein Condensates,” Eur. Phys. J. D 56, 391 (2010)

About the Author

Jeff Steinhauer is an associate professor at the Technion – Israel Institute of Technology. He specializes in condensed matter aspects of Bose-Einstein condensation, such as the Josephson effect and various types of excitations. This combination is not a coincidence, considering the subjects of his postdoctoral and doctoral research. Specifically, he did postdocs in atomic physics at the Weizmann Institute in Rehovot, Israel, as well as at MIT. In his doctoral work, he studied the Josephson effect and vortices in superfluid helium-3 and helium-4 at Berkeley, although his Ph.D. was officially from UCLA.