Matter-Wave Self-Interferometry
Since the early days of quantum mechanics, matter-wave interferences with their mind-boggling implications have fascinated generations of physicists. Today we can coherently split and combine beams of electrons, neutrons, atoms, or even large clusters, and make them interfere. The study of these interferometers is motivated by a wide variety of applications, ranging from fundamental physics, such as the study of gravity, to applications, such as global positioning and geodesy, and also provided part of the research honored with the Nobel Prize in physics this year (see 12 October 2012 Focus). The usual technique involves operating an interferometer with sources providing a high flux of particles to increase the signal, while reducing the shot noise. For this and other reasons, many people still think about coherent beam splitting in statistical terms.
However, quantum mechanics teaches us that one could operate an interferometer with single particles rather than beams because particles can interfere with themselves [1,2]. Now, writing in Physical Review Letters, Paul Parazzoli and colleagues [3] at Sandia National Laboratories, New Mexico, have realized a new scheme for an interferometer that demonstrates single-particle control in a free-space atom interferometer (Fig. 1). The principle of self-interfering atoms has even been demonstrated in traps [4], for example; however, demonstration of this effect in a free-space interferometer has not been reported until now.
The interferometer built by Parazzoli et al. presents a new method for sensing tiny forces with localized objects by a wave-based measurement. The ability to make these measurements is a direct consequence of the free-space geometry, which uses a free-falling particle as the sensing element. It also presents a beautiful textbook experiment for interferences established with a single particle.
While cooling the ensemble, they switched on a dipole trap with a tight focus at the optical resolution limit [5]. They used a so-called magic wavelength [6], at which the dynamical Stark effect induced by the trapping laser is identical for both the ground state and the excited state employed for laser cooling. This approach made the cooling across the Gaussian intensity profile of the trap as efficient as in free space. Its tight focus helped to reduce the number of trapped atoms and to end up with a single particle in a reliable way.
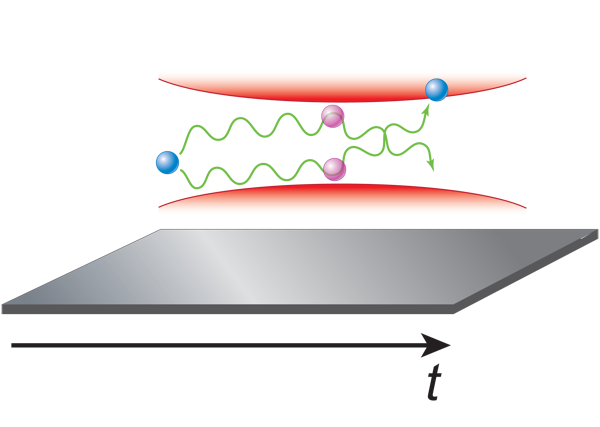
Their interferometer is based on a flexible and, today, wide-spread concept for an atom interferometer that was invented by Christian Bordé, Mark Kasevich, and Steven Chu [7,8]. In this approach, the superposition of two momentum states of an atom is created by driving its internal states with counterpropagating laser beams in a Raman-type, two-photon process. The interferometer employed by the authors comprises three Raman pulses. Depending on the pulse type, the particle ends up either (A) in a superposition state of moving with the initial momentum and at the same time being deflected by two photon recoil momenta or (B) being just deflected by two photon recoil momenta.
With these processes one can realize beam splitters and mirrors for atoms and combine these elements in a so-called Mach-Zehnder interferometer. The interferometer is composed of three consecutive Raman pulses, A-B-A, representing the following optical elements: a beam splitter, a mirror, and another beam splitter, where the two waves are recombined and mixed, forming two exit ports. Depending on the relative phase accumulated along the two trajectories, the atom ends up with a certain probability in one of the two exit ports of the interferometer. The interference pattern is revealed by repeating the experiment many times.
The temperature of the atom can be deduced from the coherence length. In order to determine the coherence length of the particle in their Mach-Zehnder interferometer, the authors varied the path length difference between both interferometer arms [9]. For this purpose, they changed the time between the first and the second, and the second and the third laser pulse. In each exit port of this asymmetric interferometer, two wave packets appear and are separated according to their path length difference. When the difference exceeds the coherence length, the contrast of the interference signal vanishes, and averaging over many experiments results in equal population in both output ports. The coherence length for thermal atoms is directly proportional to the expansion velocity of the cloud, due to the de Broglie relation, and thus it provides a measure for the statistical temperature of the atoms generated over many experiments.
The authors also employed their interferometer for measuring the gravitational acceleration of the freely falling atom and could in this way quantify the sensitivity of their device to measure a force. Moreover, they envision other interesting cases to exploit the “wavy” features of single particles, such as the measurement of the Casimir-Polder effect, which occurs between atoms close to a surface [10], or measuring gravity at close distances [11]. Their method might also be of interest for analyzing, with a high spatial resolution, the interactions between particles and surfaces, or for performing atomic quantum optics. For these purposes they suggest combining additional methods to enhance the sensitivity of their device. Having achieved a single-particle interferometer, they obviously do not want to do this by using more atoms, but rather by making them colder and reusing them by employing nondestructive detection techniques. Interferences obtained with a frequently reused single particle detected with this method will be even more intriguing, especially in light of similar experiments on single photons reused in nondemolition experiments.
References
- A. Tonomura, J. Endo, T. Matsuda, T. Kawasaki, and H. Ezawa, “Demonstration of Single-Electron Buildup of an Interference Pattern,” Am. J. Phys. 57, 117 (1989)
- H. Rauch, W. Treimer, and U. Bonse, “Test of a Single Crystal Neutron Interferometer,” Phys. Lett. A 47, 369 (1974)
- L. P. Parazzoli, A. M. Hankin, and G. W. Biedermann, “Observation of Free-Space Single-Atom Matter Wave Interference,” Phys. Rev. Lett. 109, 230401 (2012)
- C. Monroe, D. M. Meekhof, B. E. King, and D. J. Wineland, “A Schrödinger Cat Superposition State of an Atom,” Science 272, 1131 (1996)
- S. J. M. Kuppens, K. L. Corwin, K. W. Miller, T. E. Chupp, and C. E. Wieman, “Loading an Optical Dipole Trap,” Phys. Rev. A 62, 013406 (2000)
- Y.-N. Zheng, X.-J. Zhou, J.-B. Chen, X.-Z. Chen, “Magic Wavelength for Caesium Transition Line –” Chinese Phys. Lett. 23, 1687 (2006)
- M. Kasevich and S. Chu, “Atomic Interferometry Using Stimulated Raman Transitions,” Phys. Rev. Lett. 67, 181 (1991)
- Ch. J. Bordé, “Atomic Interferometry with Internal State Labeling,” Phys. Lett. A 140, 10 (1989)
- B. Saubaméa, T. W. Hijmans, S. Kulin, E. Rasel, E. Peik, M. Leduc, and C. Cohen-Tannoudji, “Direct Measurement of The Spatial Correlation Function of Ultracold Atoms,” Phys. Rev. Lett. 79, 3146 (1997)
- J. M. McGuirk, D. M. Harber, J. M. Obrecht, and E. A. Cornell, Phys. Rev. A 69, 062905 (2004)
- P. Wolf, P. Lemonde, A. Lambrecht, S. Bize, A. Landragin, and A. Clairon, “From Optical Lattice Clocks to the Measurement of Forces in the Casimir regime,” Phys. Rev. A 75, 063608 (2007)