Helium Puddles Near Absolute Zero
Helium has always been a bit of an outsider on the Periodic Table. Its two isotopes, helium- and helium- , remain liquid down to absolute zero and have the lowest liquefaction temperature among the gases. These features can be traced to the high zero-point energy relative to their attractive potential. In two dimensions, helium-4 will form a liquid and become superfluid at temperatures that depend on the density. Contrary to this, the state of helium- as a two-dimensional gas is not known. Many theories predict that in two-dimensions helium- is the only material that will stay gaseous in the ground state. However, a minority view is that a liquid phase in 2D helium- might indeed exist [1], and certain measurements seemed to support this idea [2]. New experiments looking at the specific heat of helium- adsorbed on a graphite surface provide additional evidence for helium-3 existing as puddles at temperatures below about millikelvin ( ) [3]. This may be the lowest density liquid in nature, say authors Daisuke Sato and colleagues from the University of Tokyo in Japan, reporting in Physical Review Letters. Understanding the nature of this transition will lead to a better understanding of the interactions that lead to the formation of this liquid phase—and perhaps other phases—much like understanding the interactions in ordinary gases leads to an understanding of the existence of their critical point.
Two-dimensional helium- cannot be realized experimentally unless one has a suitable substrate upon which to adsorb the atoms. Ideally, this substrate will let the helium- move freely in two dimensions—either spreading out over the surface as a gas or aggregating into a self-bound liquid. But invariably the substrate will play some role in the helium- behavior. For example, a crystalline substrate can cause the helium- to form a two-dimensional solid or registered phases.
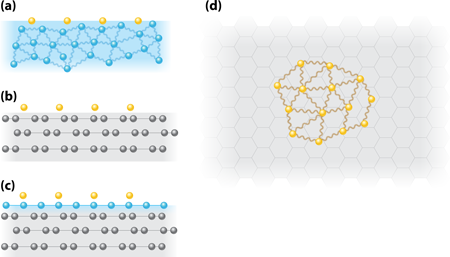
For this reason, a number of experiments on 2D helium- have used the free surface of bulk liquid helium-4 as a substrate [see Fig. 1(a)]. One might consider this helium- surface as ideal a substrate as one could have—a superfluid that, at low temperatures, is very nearly in its ground state and provides no underlying crystalline structure that might affect the helium- behavior. Studies in the 1970s of -on- found no evidence of liquid formation in measurements of the surface tension and surface sound (a two-dimensional density wave in the helium- ) for helium- surface densities of and particles per nanometer squared ( ) [4]. The data were understood in terms of the helium- acting as a 2D gas with an effective mass of times the bare mass and a surface binding energy of relative to dissolution into the underlying helium- . Besides this effective mass, other influences from the helium- substrate include interactions between helium- atoms mediated by native excitations of the helium- surface, called ripplons.
A variation of the -on- motif is to use multilayer films of liquid helium- on a solid substrate rather than the surface of the bulk. This reduces some of the bulk effects but also introduces new variables into the problem. Specifically, the density of the helium- adsorbed on a substrate does not vary smoothly with coverage but has oscillations in the density [5], and there are variations with coverage in the normal excitations of the helium- film. Thus helium- introduced on such film will have an environment that depends strongly on the underlying helium- thickness. The existence of a 2D surface state for helium- on films and the change in the spectrum of the excited states with helium- thickness were shown in Ref. [6]. Subsequent measurements (performed by myself and colleague Bidyut Bhattacharyya) of the specific heat of helium-3 on thinner films of helium-4 showed a transition, which was interpreted as the formation of a denser liquidlike phase [2]. This transition took place near for helium- densities below particle per . Later experiments [7] could not confirm the presence of a helium- liquid state, but neither were they analyzed according to the expected behavior of a 2D Fermi gas. Possible support for the condensation hypothesis has come from separate measurements of the superfluid fraction in - films [8].
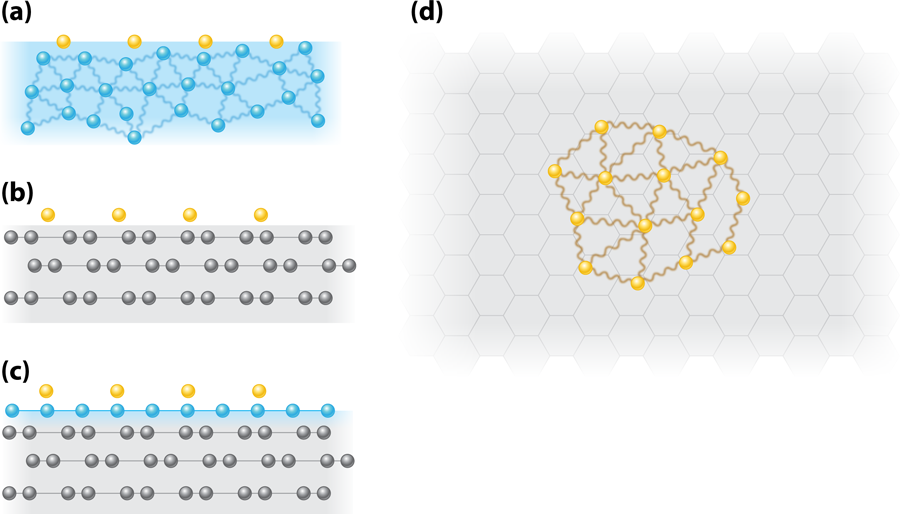
To address these issues again, Sato et al. [3] have revisited the specific heat measurements but with a new substrate. They begin by adsorbing helium- directly on a graphite surface [see Fig. 1(b)]. Graphite provides a more uniform surface than previously used solid substrates. This is important because heterogeneities can mask the 2D behavior by providing trapping sites for the helium- . The authors measure the heat capacity at various temperatures and densities using an adiabatic calorimetry technique whereby the sample is thermally isolated using a superconducting heat switch. This is effective up to a temperature of about . To determine whether a liquid phase is present, the authors measure how the heat capacity varies with temperature. The heat capacity of an ideal 2D degenerate Fermi gas or liquid on a surface of area is given by . This is independent of the number of atoms, but the extensive nature of is given by the proportionality to the occupied area . In a measurement with a given calorimeter the geometric area will be fixed. However, if there is condensation of the 2D gas into a liquid occupying a subset of the area [see Fig. 1(d)], then, with the assumption that the effective mass does not change, the slope of the heat capacity as a function of temperature will decrease. This is because the in the above equation is replaced by the smaller area .
Based on their analysis of the data, Sato and colleagues conclude that below temperatures of , the helium- is in a 2D liquid state with a density around particle per . This implies that the helium- atoms are binding together into a liquid despite having very large interatomic distances of roughly particle per . Subsequent measurements with layers formed on top of a monolayer of solid helium- also show similar behavior [see Fig 1(c)]. One may view the helium- as a buffer layer that eliminates any residual surface heterogeneity of the graphite. In all of these measurements, however, the heat capacity could not be measured above because of their particular superconducting heat switch. Thus Sato et al. are not able to observe the actual transition from the gaseous state into the liquid state, as was measured in Ref. [2].
So where is one left with this issue of 2D gas vs 2D liquid? Clearly these newly reported measurements must be extended to higher temperatures to see explicitly the transition from gas to liquid. It will be interesting to find out whether the heat capacity has a significant jump at the transition (as one would expect), or if it changes with a minimum jump as observed in Ref. [2]. The latter case would imply missing entropy, which could be bad or good: bad, because it might betray a metastability in the system; good, because it might suggest that other transitions occurring at yet lower temperatures are responsible for this missing entropy. These transitions could perhaps be a dimerization [9], or pairing, of the helium- atoms already in the liquid state. Further, these pairs—being Bosonic—could form a superfluid state [10]. This would be an exciting endgame.
What about theory? As pointed out by Sato et al., theoretical considerations weigh against the formation of a self-bound liquid state for . Thus a further confirmation of these results would pose a theoretical challenge for future calculations. Stay tuned.
References
- A. F. Andreev and D. A. Kompaneets, “Gas-liquid Phase Transition in the System of Surface Impurities of in Superfluid Solutions,” Zh. Eksp. Teor. Fiz. Pis’ma Red 17, 376 (1973) [JETP Lett. 17, 268 (1973)]
- B. K. Bhattacharyya and F. M. Gasparini, “Observation of Two-Dimensional Phase Separation in - Films,” Phys. Rev. Lett. 49, 919 (1982); “Phase Transition of Two-Dimensional from a Dilute to a Dense Phase,” Phys. Rev. B 31, 2719 (1985)
- D. Sato, K. Naruse, T. Matsui, and H. Fukuyama, “Observation of Self-Binding in Monolayer ,” Phys. Rev. Lett. 109, 235306 (2012)
- J. R. Eckhardt, D. O. Edwards, P. P. Fatouros, F. M. Gasparini, and S. Y. Shen, “Spin-Rotation Coupling in the Alkali—Rare-Gas Van der Waals Molecule KAr,” Phys. Rev. Lett. 32, 507 (1974); D. O. Edwards, S. Y. Shen, J. R. Eckhardt, P. P. Fatouros, and F. M. Gasparini, Phys. Rev. B12, 892 (1975)
- E. Krotscheck, “Liquid Helium on a Surface: Ground State, Excitations, Condensate Fraction, and Impurity Potential,” Phys. Rev. B 32, 5713 (1985)
- M. J. Di Pirro and F. M. Gasparini, “Two-Dimensional in Films,” Phys. Rev. Lett. 44, 269 (1980)
- Pei-Chung Ho and R. B. Hallock, “Heat-Capacity Studies of in - Mixture Films and the Coverage Dependence of the Two-Dimensional Landau Fermi-Liquid Parameters,” Phys. Rev. Lett. 87, 135301 (2001); H. Akimoto and R. B. Hallock, “Heat Capacity Measurements of - Mixture Films,” J. Low Temp. Phys. 138, 257 (2004)
- G. A. Csathy, E. Kim, and M. H. W. Chan, “Condensation of and Reentrant Superfluidity in Submonolayer - Mixture Films on ,” Phys. Rev. Lett. 88, 04530 (2002)
- E. P. Bashkin, ” van der Waals Molecular Dimers in Solutions of the Quantum Liquids -,” Zh. Eksp. Teor. Fiz. 78, 360 (1980) [Sov. Phys. JETP 51, 181 (1980)]; E. Krotscheck, J. Paaso, M. Saarela, and K. Schörkhuber, “Phases of - Mixtures in Two Dimensions,” Phys. Rev. B 64, 054504 (2001)
- A. V. Chubukov and A. Sokol, “Theory of -wave Pairing in a Two-Dimensional Fermi Gas,” Phys. Rev. B 49, 678 (1994)