A Cut Above the Rest
Experienced chefs know that to make a neat cut in a boiled egg or a piece of cheese, a thin wire, or even a fine piece of thread, can work better than a knife. But even a blunt knife can cut soft solids well if it is rocked back and forth while applying a gentle pressure. Understanding the balance of forces needed to make a clean cut into deformable materials could be important for developing highly efficient techniques in industrial-scale food processing, or new tools for cutting biological tissue for analysis or during surgery. Writing in Physical Review Letters [1], Etienne Reyssat, at Harvard University, and colleagues provide an intriguing analysis of the cutting of soft solids, applying a combination of theory and experiments to pinpoint the role played by shear in facilitating the fracture of a highly deformable material.
Why do soft materials require such a peculiar cutting technique? Part of the answer lies in the properties of certain types of soft solids [2], such as rubber, that exhibit a nonlinear relationship between applied stress and the resulting strain (deformation). They can, for instance, stiffen when they are deformed by a large amount. If one attempts to cut such a material by slicing it, the friction with the cutting blade induces a shear strain, which generates a normal stress (directed inward in the rubber) that is proportional to the square of the shear strain [2]. This effect can lead to counterintuitive behavior, akin to that observed in Chinese finger traps: in such toys, when the victim inserts a finger inside a rubber tube, the finger gets trapped. The more one tries to pull out the finger, the larger is the generated normal stress, which tightens the trap even more. This sort of nonlinear feedback can lead to a frictionally locked situation, especially when the friction coefficient (the ratio of normal to shear stress) is very high. If this nonlinearity is the dominant mechanism, as happens when cutting a strain-stiffening solid with a blade that is not sufficiently sharp, the locked state is released in a catastrophic way by the formation of cracks that develop at the interface and then penetrate the bulk of the solid, generally leading to a messy, improper cut. This is why using a thin cutting wire avoids the problem considerably: since its area of contact with the solid is much smaller than that of a knife, the relevance of friction-induced normal stress is reduced and the crack forms more precisely around the cutting wire.
This argument mainly applies to extremely nonlinear materials, but friction can impact the cutting of soft solids in other ways and a more complete analysis is required. Atkins et al. [3] argued that friction affects the optimal “slice-to-push” ratio needed for cutting the solid without squishing it too much, and highlighted the role of friction in the post-fracture stage, once the crack starts to develop. Now, the study of Reyssat et al. [1] shows that friction plays a crucial role in the very first stages of cutting, by enabling, right below a cutting blade, the large stress concentration that is needed for cracks to nucleate. The authors’ arguments apply to a broad class of soft solids, including gels, for which, within certain limits of applied strain, not much stiffening occurs, or the stiffening effect cannot be exploited, since friction with typical cutting materials does not reach a very high value. So how does a cutting wire generate the stress concentration that causes fracture? For hard, brittle solids, preexisting flaws can grow into cracks when an external force is applied. But in soft solids, such flaws are usually in the form of small air bubbles, which cannot readily grow into sharp cracks. In soft polymeric materials such as gels, one way for fracture to occur is via stress-assisted crack nucleation. In gels, the load bearing elements are the chains of the polymer network, which can break by the combined action of deformation forces and thermal fluctuations. If a polymer chain of spring constant ks is stretched by an amount x, the probability of its rupture increases by the factor exp(ksx2/2kBT), where kBT is the thermal energy [4]. When one polymer chain breaks, the nearby chains are further stretched and their fracture rate is increased in a cascading fashion. The process continues, accompanied by increase of tension in each surviving chain until the energy barrier to bond breakage is vanishingly small; at this point, all the remaining chains break simultaneously and a macroscopic crack is formed. If the stretch of the chain can be enhanced, the argument of the exponential term would increase (by a factor of 4 if the stretch is doubled), resulting in a dramatic enhancement of rupture rate, provided that the energy stored per chain is greater than kBT.
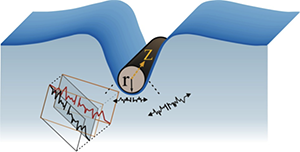
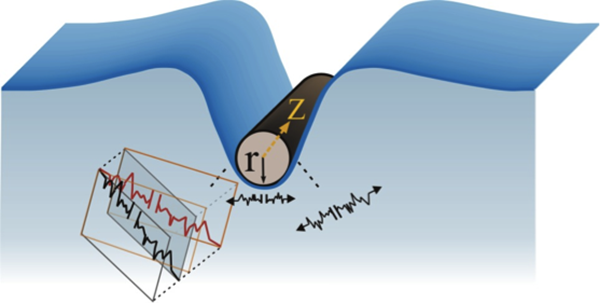
This type of fracture is exactly the focus of Reyssat et al.’s work, which analyzes how the polymer stretch (hence the efficiency of the cutting) can be optimized by applying the proper combination of the proper combination of slicing action and pressure. The authors use a simple setup in which a soft gel is cut by a thin metal wire that moves both towards the sample (thus applying a downward normal force) and in a tangential direction (thus providing slicing action). The occurrence of a fracture cut is studied as a function of the ratio of tangential to normal speed of the wire and interpreted by use of continuum-mechanics simulations, using an appropriate constitutive law for the nonlinear solid. When no slicing action (i.e., no shear) is applied, the authors find that a high normal force is needed before the wire cuts through the gel, as the wire has to indent into the gel very deeply to reach the tensile stress that induces fracture. However, in the slicing mode, the normal force needed to initiate a crack is reduced considerably: shear allows reaching the same local critical stress using a much smaller normal displacement and pushing force.
A possible explanation of this phenomenology is illustrated in Fig. 1. When a cylindrical wire is pushed down onto the solid (in a normal direction), its surface is stretched in the neighborhood of the wire perpendicular to its long axis and mostly the chains that are below the interface are stretched. But if the wire is moved simultaneously along the Z direction, the polymer chains under and around the wire experience additional tension. As a consequence, the induced stretching is more symmetrically distributed around the wire and the additional stretch, compared to the normal-pushing case, amplifies the fracture rate exponentially, as described above.
These results will inspire further research on the subject. For example, one can imagine embedding tracer particles in the solid and mapping out various properties of the system, such as the internal strain and stress fields, the crack patterns that are produced and their dependence on the relative weight of the slicing and pushing force. Finally, although the current analysis assumes a horizontal cutting wire, the framework proposed in this paper could be applied to analyze the more general case of an oblique wire, as in most cutting schemes, and to test the hypothesis [3] that cutting “downhill” is more efficient than cutting “uphill.”
The work of Reyssat et al. provides a quantitative explanation of cutting features encountered in many real-world examples of soft-solid cutting. More importantly, it may be a step towards a predictive framework that connects the outcome of a cutting operation with the geometry and materials of a given cutting apparatus.
References
- E. Reyssat, T. Tallinen, M. Le Merrer, and L. Mahadevan, “Slicing Softly with Shear,” Phys. Rev. Lett. 109, 244301 (2012)
- A. N. Gent, “Friction and Wear of Highly-Elastic Solids,” Wear 29, 111 (1974)
- A. G. Atkins, X. Xu, and G. Jeronimidis, “Cutting, by ‘Pressing and Slicing,’ of Thin Floppy Slices of Materials Illustrated by Experiments on Cheddar Cheese and Salami,” J. Mat. Sci. 39, 2761 (2004)
- H. Eyring, “Viscosity, Plasticity, and Diffusion as Examples of Absolute Reaction Rates,” J. Chem. Phys. 4, 283 (1936)