NMR Looks Deep Inside Nooks and Crannies

Beau Webber

Viewpoint

NMR Looks Deep Inside Nooks and Crannies

School of Physical Sciences, University of Kent, Canterbury CT2 7NJ, United Kingdom

January 31, 2012• Physics 5, 14

An NMR technique tracks the diffusion of water molecules to obtain micron-scale structural information about a porous material.

Figure caption — **Figure 1:** NMR can determine the size of pores in materials, such as this sandstone core, by analyzing the diffusion of water inside the pores.

Nuclear magnetic resonance (NMR) imaging is an attractive tool for studying structured matter because it is both nondestructive and can “see into” optically opaque materials. The technique has developed into an important diagnostic tool for analyzing geological systems (Fig. 1), particularly in efforts to recover oil and gas from rock beds.

Where magnetic resonance imaging is limited is in resolving structural details on the micron or nanometer scale, a capability that would be desirable for simulating the flow of oil, water, and gas through porous rocks. The main limitation is often signal to noise. To have sufficient signal, NMR samples typically need to have a volume of $100$ microliters, but in a $10$ micrometer ( $μ m$ ) diameter pore, the volume is less than a picoliter, and in a $10$ nanometer (nm) diameter pore the volume is down to less than $10^{- 21}$ liter. Any technique that could obtain information about the average pore size and shape in a structure by analyzing the entire sample, as opposed to trying to measure each pore individually, would be welcomed.

A paper appearing in Physical Review Letters from Noam Shemesh and his colleagues at Tel Aviv University in Israel describes such an advance in magnetic resonance imaging that may allow for imaging both the size and shape of micron-sized canals in a porous material [1]. Their technique, which they have tested on a bundle of microcapillaries containing water, uses NMR to gather information about the diffusion of water molecules that are bounded by pore walls. Though their new method has so far only been tested on an idealized structure containing identical capillaries, Shemesh et al.’s results represent a first for NMR imaging of microporous structures.

In a typical NMR experiment, the resonant frequency or relaxation time of nuclear spins in a material, in the presence of a magnetic field, is measured to learn about the environment of those spins. As applied to studying the structure of porous materials, the approach is fairly simple: pores are filled with water and NMR is used to study the behavior of the protons in the water.

Since the 1970s, the use of NMR to study liquids within porous materials has developed along two, mostly distinct, lines [2–4]: direct imaging and indirect, or diffusional, measurements. In its simplest form, direct imaging, which is probably the most familiar because of its applications in medicine, involves applying magnetic field gradients at a series of points in a sample, and performing a measurement at each point. An alternative that gives indirect information is a diffusion technique, where NMR tracks the effects of pore walls on the migration of water molecules. This can be used to study both the properties of the liquid in the pores and the size of the pores.

A number of other techniques have developed to study structure. NMR relaxometry, for example, takes advantage of the fact that if diffusion carries a water molecule into close proximity to a pore wall, then phase information about the molecule’s spin may be lost. Thus, in small pores, water has a shorter so-called transverse (spin-spin) relaxation time, or $T_{2}$ , than in bulk liquid. NMR relaxometry has been heavily applied to determining pore-size distributions in rock systems for oil recovery. The technique has two problems though: the pore surface relaxation parameters must be known [5] and an ill-defined inverse problem of converting a set of overlapping exponential time decays to a set of pore sizes has to be solved. Another approach is NMR cryoporometry (NMRC) [6], which measures how nanostructuring affects a property of water, such as its melting point.

Building on previous work [7], Shemesh et al. have brought together both the direct and indirect approaches to study a microporous structure. Their method is based on “spin echo” measurements, so it is worth explaining this basic technique first. As in most NMR experiments, the first step is applying a strong, constant, and uniform magnetic field, which will (at equilibrium) align the spins in a sample along the direction of the field (the $z$ direction). Applying a strong radio frequency (rf) pulse in the transverse direction flips the spins $90$ degrees and they precess in the $x$ - $y$ plane at the NMR resonant frequency. A sensitive pickup coil can measure the tiny rf signal from the precessing spins, but local magnetic fields cause the rotating spins to get out of phase with one another, with some spins precessing faster and some slower, so the net signal in the pickup coil starts to decay. However, it is also possible to apply a second rf pulse that refocuses the spins, giving rise to an observable spin echo in the pickup coil.

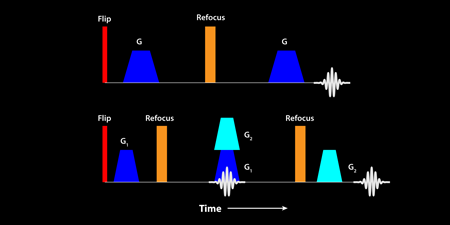
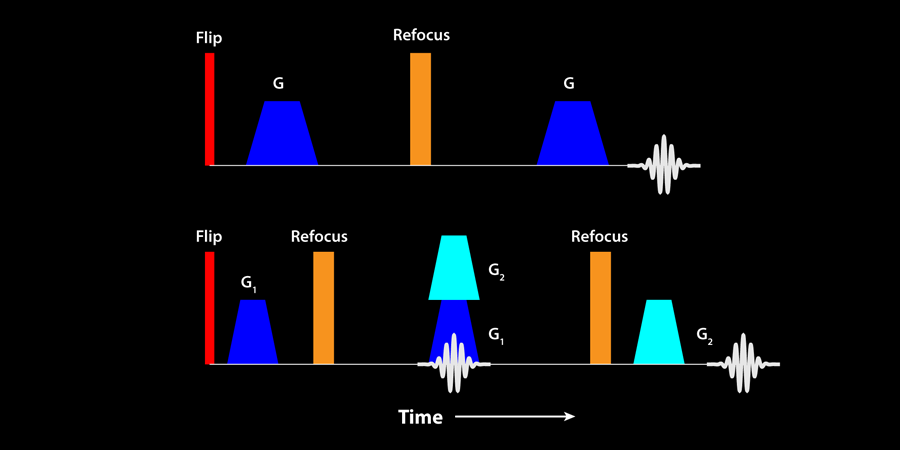
The time dependence of the spin-echo signal from water molecules confined to pores is known to provide some information about the size of the pores. More information can be gained by applying a pulsed magnetic field gradient before and after the refocusing pulse (Fig. 2, top). The first field gradient pulse acts to “wind up” the phase of the spins and effectively labels the position of the spins, based on the strength of the field. The second gradient pulse, which appears after a delay time, acts to unwind the spins. If the spins have not moved, an identical echo signal in the pickup coil is formed. However, if the spins have moved, the spins do not all re-phase as well, and the echo amplitude is reduced. By varying the delay between the two gradient pulses one can probe the distance the spins have moved, and if they are in a bounded pore, one can obtain information on the pore dimensions, but not the full pore shape, since phase information is lost.

It is also possible to do a double pulse-gradient spin-echo experiment, in which two further gradient pulses are added (Fig. 2, bottom). If the second and third gradient pulses are coincident, one has two characteristic times that may be varied to probe the system. If the porous system is highly ordered, then one can show (see Ref. [2]) that, because phase information is preserved in this experiment, the spin-echo signal contains information about the pore shape, as well as its size.

Shemesh et al. combine a conventional single pulse-gradient spin-echo (PGSE) measurement with a double PGSE measurement on the entire volume of water contained in a bundle of microcapillaries, each with an internal diameter of $23 μ m$ , and show they can extract both the size and the shape of these pores [4,8]. To obtain a one-dimensional projection image of the average pore microstructure, they divide the decaying spin-echo signal from the double-PGSE measurement by that from the single-PGSE experiment, and take a Fourier transform of the resulting function. To get a 2D projection of the pore, they project the 1D result through $360$ degrees.

There are interesting steps for the future. For example, one might ask whether the technique will produce a reasonable image of the “average” pore size in a more realistic system that has a range of pore diameters. Better yet, is there some manner in which a pore-image distribution can be obtained? Many systems, like porous rock, aren’t fully restricted by a simple boundary, and it will be important to establish if this new technique can still image an “average” pore and probe the structure of the tortuosity via the diffusion from the pore.

References

N. Shemesh, C-F. Westin, and Y. Cohen, Phys. Rev. Lett. 108, 058103 (2012)
Paul T. Callaghan, Principles of Nuclear Magnetic Resonance Microscopy (Clarendon Press, Oxford, 1993)[Amazon][WorldCat]
Rainer Kimmich, NMR Tomography, and Diffusometry, Relaxometry (Springer-Verlag, Berlin, 1997)[Amazon][WorldCat]
Paul T. Callaghan, Translational Dynamics and Magnetic Resonance Principles of Pulsed Gradient Spin Echo NMR (Oxford University Press, Oxford, 2011)[Amazon][WorldCat]
J. H. Strange, J. Mitchell, and J. B. Webber, Magn. Reson. Imaging 21, 221 (2003)
J. H. Strange, M. Rahman, and E. G. Smith, Phys. Rev. Lett. 71, 3589 (1993)
N. Shemesh and Y. Cohen, Magn. Reson. Imaging 195, 153 (2008)
J. Mitchell, T. C. Chandrasekera, M. L. Johns, L. F. Gladden, and E. J. Fordham, Phys. Rev. E 81, 026101 (2010)

About the Author

Beau Webber is an Honorary Research Fellow at the University of Kent’s School of Physical Sciences in England, and in recent years has held a similar position with the Institute of Petroleum Engineering at Heriot-Watt University in Scotland. He is the director of Lab-Tools in Canterbury. Lab-Tools is a micro-SME (the European Union’s term for small company) that does nanometric studies and nanometrology analyses for and with research organizations, universities, and companies, on a worldwide basis. His research interests include the study of matter that is structured on the nanoscale to microscale using NMR and neutron scattering.