A Glance at the Earliest Universe
Cosmological inflation, the hypothesis that the early Universe underwent an extremely rapid expansion, is a popular paradigm in modern cosmology. The theory successfully explains how quantum mechanical fluctuations of the vacuum, starting about 10-36 seconds after the big bang, could have given rise to the large-scale structure of our Universe, leading to predictions that have been confirmed by a range of cosmological observations. However, inflationary cosmology cannot be the ultimate theory of the Universe. If one projects the Universe backward in time, it gets so hot and dense that the laws of physics on which inflation is based (classical general relativity) break down. In the so-called Planck era, lasting up to one Planck second ( 10-43s) after the big bang, the force of gravity would have reached values comparable to the other fundamental forces. In this regime, quantum gravity effects would have been important, creating conditions that go beyond the conventional understanding of space and time.
What conditions existed prior to inflation and to what extent do they affect the predictions of the inflationary model? Such fundamental cosmological questions remain unanswered, since we don’t yet have a theory that can tackle the physics of the preinflation era and smoothly connect it to the inflationary period. Writing in Physical Review Letters, Ivan Agullo and colleagues at Pennsylvania State University in University Park, take loop quantum gravity (LQG)—one candidate theory of quantum gravity—and use it to extend the inflationary scenario all the way to the Planck era [1]. The authors also find that features of the preinflationary phase could result in observable cosmological signatures, thus providing an opportunity to test quantum gravity and probe preinflationary physics in future astronomical observations.
In the 1980s, Guth, Linde, Albrecht, and Steinhardt proposed the theory of cosmological inflation [2] to explain two puzzles in the big bang model of cosmology: why our Universe is approximately flat (i.e., it can be described as a Euclidian space, with a vanishingly small curvature) and why very distant regions in our Universe appear to have a nonrandom correlation in their temperatures (which suggests they were once causally connected). Inflation provides answers to these questions by postulating that the volume of the Universe rapidly expanded by a factor of at least 1078 in an early period of cosmic evolution. Many models of inflation exist, but qualitatively they all lead to similar physics: during inflation, quantum fluctuations of the vacuum lead to density fluctuations that acted as the seeds of the large-scale structure of the present Universe. Since these density fluctuations were accompanied by temperature fluctuations, they left an observable imprint on the cosmic-microwave-background (CMB) radiation—the thermal radiation released once the Universe expansion allowed photons to travel freely in space. The predictions made by the inflationary theory have been largely confirmed by state-of-the-art CMB measurements [3].
Despite its remarkable successes, the theory of inflation has several problems. The first is the so-called “singularity problem.” In 2003, Borde et al. showed that inflation predicts that the Universe, when evolved backward in time, would shrink to a point—the big bang singularity—at which energy density, spacetime curvature, and temperature are infinite [4]. Since general relativity breaks down under these conditions, the current inflationary theory cannot remain valid as the singularity is approached. Another difficulty is the “trans-Planckian” problem [5]: according to inflation, current cosmological scales could have developed from features that were smaller than the Planck length at the onset of inflation. The Planck length (the distance traveled by light in 1 Planck second) is the natural length scale in the Planck era. But on such a small scale, the classical description of spacetime and gravity is believed to be invalid.
At the high densities and energies of the preinflationary regime, it is expected that quantum effects on the force of gravity come into play. Under such conditions, a new quantum theory of gravity, yet to be completed, is needed to describe the “microstructure” of spacetime, similar to the way quantum mechanics describes the microstructure of matter. Loop quantum gravity is one such attempt to merge quantum mechanics and general relativity. In LQG, the classical continuum geometry of spacetime is replaced by a quantum discrete geometry: space can be viewed as made of a fine fabric of finite “loops.”
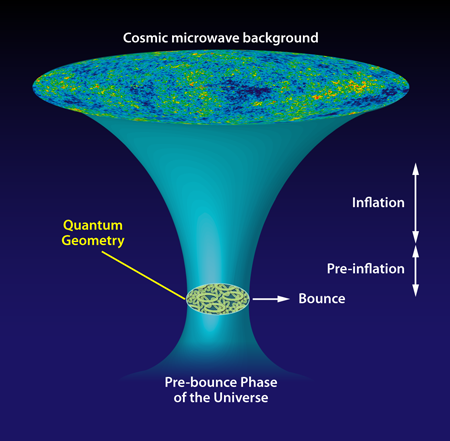
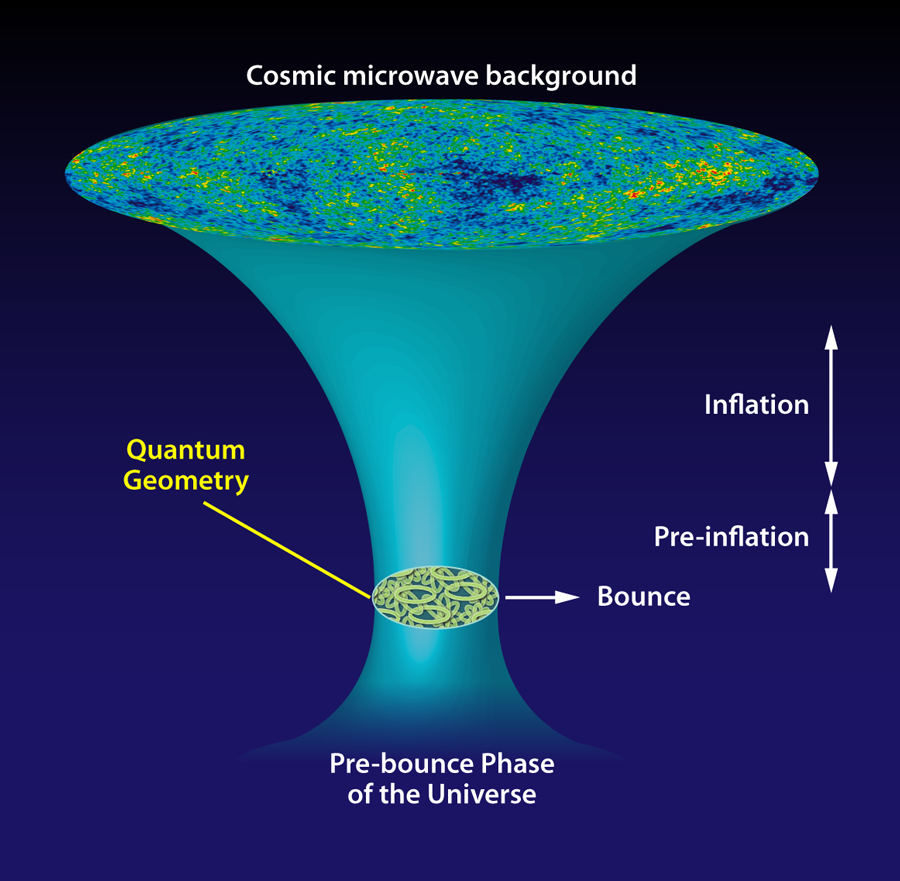
Over the past decade, LQG has been applied to cosmology (a field known as loop quantum cosmology), with the hope of understanding Planck-era physics and solving the singularity problems of different cosmological models, including inflation [6,7]. When the discreteness of space does not matter, the equations of LQG approximate classical models of cosmology extremely well (much like quantum mechanics merges into classical physics when quantum effects are negligible). Yet differences arise when the curvature of the spacetime starts to be significant. In LQG, the Universe does not emerge from a singularity. Instead, the big bang is replaced by a “big bounce”: the beginning of a period of expansion that followed a period of contraction of a previous phase of the Universe [6].
The work of Agullo et al. adopts the bounce paradigm of LQG and thus it is free of the singularity problem. Their key physical idea is that in the phase close to the bounce, vacuum fluctuations occurred over a nonclassical, quantized spacetime geometry in a tiny volume of approximately 103 cubic Planck lengths. These are the fluctuations that act as the seeds of the large-scale structure of our Universe. Since a full theory of quantum gravity is not yet available, the authors had to restrict themselves to an approximation: they treat fluctuations with standard quantum field theory (as in inflationary cosmology), but they take advantage of recent theoretical results [8] and study how these fluctuations evolve in a spacetime that is quantized by LQG techniques. Since the inflationary paradigm is extended via LQG to the Planck-era, trans-Planckian inconsistencies are also resolved, as LQG can treat rigorously sub-Planck lengths. One should note that the consistency of their analysis relies on one important assumption: the quantum vacuum fluctuations do not, in turn, affect the underlying quantum geometry. The authors show that this is true for a large class of possible initial conditions, for which vacuum fluctuations at the onset of inflation turn out to be essentially the same as the ones considered in the standard inflationary. Their LQG-based model, schematically illustrated in Fig. 1, is thus consistent with the predictions of inflationary theory and extends it in a continuous way to the Planck era.
However, for a narrow subset of such initial conditions, the LQG-predicted vacuum state can be subtly different from the one assumed in inflation. This would lead to potentially observable signatures of quantum gravity [9] that could be revealed in high-precision CMB experiments as non-Gaussian statistical properties of the temperature distribution (which are expected to be distinct from the predictions of standard inflationary models). Should future observations confirm LQG predictions, a so-far-inaccessible era of the early Universe would become accessible to observational cosmology.
Being able to look at the very early Universe, when gravity was on par with the other forces, may well hold the key for a fully consistent theory that unifies general relativity and quantum mechanics.
References
- I. Agullo, A. Ashtekar, and W. Nelson, “Quantum Gravity Extension of the Inflationary Scenario,” Phys. Rev. Lett. 109, 251301 (2012)
- A. Guth, “Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems,” Phys. Rev. D 23, 347 (1981); A. Linde, “A New Inflationary Universe Scenario: A Possible Solution of the Horizon, Flatness, Homogeneity, Isotropy, and Primordial Monopole Problems,” Phys. Lett. B 108, 389 (1982); A. Albrecht and P. J. Steinhardt, “Cosmology for Grand Unified Theories with Radiatively Induced 4 Symmetry Breaking,” Phys. Rev. Lett. 48, 1220 (1982)
- E. Komatsu et al. (WMAP Collaboration), “Seven-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation,” Astrophys. J. Suppl. 192, 18 (2011)
- A. Borde, A. H. Guth, and A. Vilenkin, “Inflationary Space-Times Are Incomplete in Past Directions,” Phys. Rev. Lett. 90, 151301 (2003)
- J. Martin and R. Brandenberger, “The Trans-Planckian Problem of Inflationary Cosmology,” Phys. Rev. D 63, 123501 (2001)
- A. Ashtekar and P. Singh, “Loop Quantum Cosmology: A Status Report,” Class. Quant. Grav. 28, 213001 (2011)
- M. Bojowald, “Loop Quantum Cosmology,” Living Rev. Relativity 11, 4 (2008)
- A. Ashtekar, W. Kaminski, and J. Lewandowski, “Quantum Field Theory on a Cosmological, Quantum Spacetime,” Phys. Rev. D 79, 064030 (2009)
- I. Agullo and L. Parker, “Non-Gaussianities and the Stimulated Creation of Quanta in the Inflationary Universe,” Phys. Rev. D 83, 063526 (2011); I. Agullo and S. Shandera, “Large Non-Gaussian Halo Bias from Single Field Inflation,” J. Cosmol. Astropart. Phys. 1209, 007 (2012); J. Ganc and E. Komatsu, “Scale-Dependent Bias of Galaxies and Mu-type Distortion of the Cosmic Microwave Background Spectrum from Single-Field Inflation with a Modified Initial State,” Phys. Rev. D 86, 023518 (2012)