Pairing with Spin Fluctuations
Superconductivity requires a “pairing interaction”—an indirect attractive force between the conduction electrons that can overcome their direct Coulomb repulsion. To prove which particular degrees of freedom provide this pairing interaction is supremely difficult: nearly 40 years elapsed between the discovery of superconductivity in 1911 and the “smoking gun” measurement of the isotope effect that proved that lattice distortions provide the pairing interaction in conventional superconductors, and 26 years have elapsed since the discovery of high-temperature superconductivity, and still the pairing mechanism in cuprates is hotly debated. Thus it is a remarkable step forward that NMR measurements reported in Physical Review Letters by Taisuke Hattori of Kyoto University, Japan, and colleagues [1] have provided strong evidence that ferromagnetic fluctuations provide the pairing force that leads to superconductivity in an exotic, and comparatively recently discovered [2], class of superconductors in which ferromagnetism and superconductivity seem to happily coexist. Knowledge of the pairing mechanism will lead to a deeper understanding of the superconducting states of these, and possibly other, unconventional superconductors.
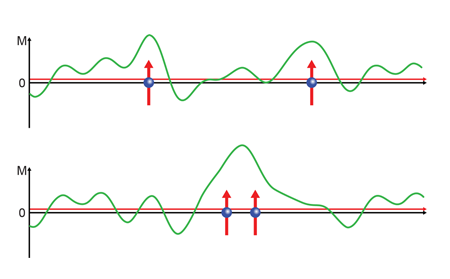
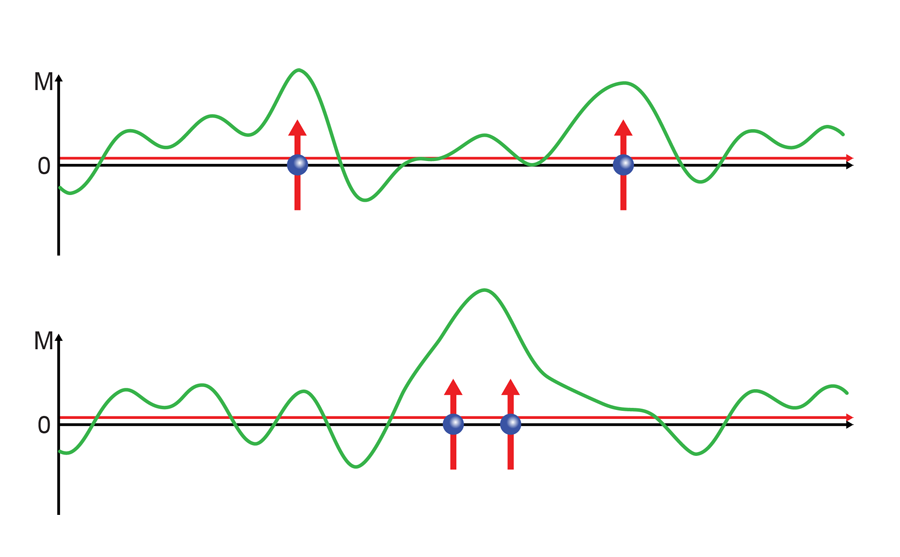
It is well known that superconductors don’t like magnetic fields. Application of a sufficiently large magnetic field will always destroy superconductivity, and in conventional superconductors such as niobium, even a tiny concentration of magnetic impurities kills superconductivity. Thus it is no surprise that ferromagnetic superconductors are very rare: only four are known, and all four are variations on a common theme. The three best studied of these, UGe2 [2], URhGe [3], and UCoGe [4], discovered in 2000, 2001, and 2007, respectively, share a number of characteristics: they all contain uranium ( U), they have very similar crystal structures, and they have rather specific magnetic properties. For example, in all three materials, the magnetism is extremely anisotropic: the magnetic moments on the uranium atoms are constrained to point parallel or antiparallel to the c axis of the crystal. Moreover, all three materials are so-called “itinerant” ferromagnets, meaning that the magnetism comes from an imbalance between the number of spin-up and spin-down conduction electrons. (This is as opposed to conceptually simpler cases such as gadolinium ( Gd), in which the magnetism comes from 4f electrons that are localized on the Gd ions, while the conduction electrons occupy s, p, and d orbitals.) It is common for itinerant ferromagnets with low magnetic ordering temperatures to have large magnetic fluctuations. That is, there can be a local imbalance of up- and down-spin electrons for a short time span that is much larger than the average imbalance (see Fig.1). UCoGe is magnetically ordered only below about 2.5 K, and when superconductivity sets in at a lower temperature of about 0.5 K, the ordered magnetic moment per U atom has only grown to about 0.05μB, much smaller than the free-ion value. The tiny magnetic moment signals that magnetic fluctuations are large, and they are directly seen in the measurements of Hattori et al.
Hattori et al. have used nuclear magnetic resonance to observe the fluctuating magnetism in UCoGe. In their measurement a magnetic field is applied which polarizes the nuclear spins on the cobalt ( Co) sites. They perturb the nuclear polarization with radio-frequency pulses and then watch it relax back to equilibrium. The key to their work is that the relaxation rate of the nuclear polarization is determined by the amplitude of magnetic fluctuations in directions perpendicular to the applied field.
With the field applied perpendicular to the c axis, Hattori et al. see rapid relaxation of the polarization, indicative of large amplitude fluctuations of the magnetization along the c axis. However, as the field is rotated towards the easy axis, the spin fluctuations are very rapidly killed off, presumably because the field converts the fluctuating moments into large static moments.
Hattori et al. are able to correlate this field-angle-dependence of the magnetic fluctuations with another striking property of UCoGe, which is that its superconductivity is exceptionally sensitive to the direction of an applied magnetic field. When the magnetic field is perpendicular to the c axis the superconductivity is very robust, surviving to around 10 tesla; however, as the field direction is rotated towards the c axis, the critical field for destruction of superconductivity falls precipitously. An obvious interpretation of this behavior would be that the component of the applied field that is parallel to the c axis induces a large magnetic polarization, and the large internal field thus generated disrupts the paired electrons either through coupling to their spins or their orbital motion. This sort of physics is very well understood (indeed this is why ordinary superconductors don’t like magnetic fields) so it can be modeled quite accurately and, surprisingly, it doesn’t fit the measurements in UCoGe. Rather, Hattori et al. argue that their results are better explained if the magnetic field is disrupting not the pairs directly, but rather the underlying pairing mechanism. This, in particular, explains the striking parallel in the suppression of the magnetic fluctuations and the suppression of the superconductivity as the magnetic field is rotated towards the c axis. It is strong evidence that magnetic fluctuations are the ones doing the pairing.
It was believed from the start [2] that fluctuating magnetism may play a key role in the superconductivity of ferromagnetic superconductors. The initial hint came from the fact that all of the ferromagnetic superconductors are very close to the border between a ferromagnetic and a nonmagnetic ground state, close to a ferromagnetic quantum critical point at which magnetic fluctuations are maximized. Indeed, theoretical proposals along these lines go back to long before the discovery of ferromagnetic superconductivity (e.g., Ref. [5]), and in another case of theoretical prescience that is very rare in the history of superconductivity, Monthoux and Lonzarich pointed out in 1999 that uniaxial anisotropy would be favorable for the occurrence of superconductivity in close proximity to itinerant ferromagnetism [6].
Figure 1 shows a cartoon version of how two electrons can be paired by longitudinal magnetic fluctuations. A material on the border of ferromagnetic order is very easily polarized. Conduction electrons have a spin, thus they polarize the surrounding background. It can be imagined that it is energetically favorable for two electrons to travel in a shared polarization cloud, and thus they become paired.
But suggesting a pairing mechanism and proving it are two very different things, hence the excitement of the new measurements [1]. In comparison with the isotope effect, which showed a systematic dependence of the superconducting transition temperature upon substitution of one isotope of an element with another, the NMR evidence is still slightly circumstantial. Eventually, detailed calculations may be able to turn this into a rigorous proof, but even if it is not yet a smoking gun, we can say that ferromagnetic fluctuations have left their fingerprints all over the scene.
References
- T. Hattori, Y. Ihara, Y. Nakai, K. Ishida, Y. Tada, S. Fujimoto, N. Kawakami, E. Osaki, K. Deguchi, N. K. Sato, and I. Satoh, Phys. Rev. Lett. 108, 066403 (2012)
- S. S. Saxena et al., Nature 406, 587 (2000)
- D. Aoki, A. Huxley, E. Ressouche, D. Braithwaite, J. Flouquet, J.-P. Brison, E. Lhotel, and C. Paulsen, Nature 413, 613 (2001)
- N. T. Huy, A. Gasparini, D. E. de Nijs, Y. Huang, J. C. P. Klaasse, T. Gortenmulder, A. de Visser, A. Hamann, T. Görlach, and H. v. Löhneysen, Phys. Rev. Lett. 99, 067006 (2007)
- D. Fay and J. Appel, Phys. Rev. B 22, 3173 (1980)
- P. Monthoux and G. G. Lonzarich, Phys. Rev. B 59, 14598 (1999)