Cloaking Comes Out of the Shadows

Ross McPhedran; Alexander Movchan

Viewpoint

Cloaking Comes Out of the Shadows

Ross McPhedran

CUDOS ARC Centre of Excellence and School of Physics, University of Sydney, New South Wales 2006, Australia

Alexander Movchan

Department of Mathematical Sciences, University of Liverpool, Liverpool L69 7ZL, United Kingdom

January 3, 2012• Physics 5, 2

Cloaking devices made of a composite of soft and hard materials can divert elastic vibrational waves around an object as though it wasn’t there.

Figure caption — **Figure 1:** A device for cloaking an object from elastic waves in a flexible medium. (a) The cloaking ring designed by Stenger *et al.* consists of concentric rings of a hard plastic, punctured with holes that are filled with a softer silicone-based material. (b) Images of $200 Hz$ elastic waves passing around an inclusion (dark circle). Without the cloak (left), the waves break up; with the cloak (right), shown here by a dotted line, the waves pass by mostly undisturbed. (The white scale bar is 5 cm.)

Though cloaking devices are mainly associated with hiding objects from light, the concept of cloaking is not restricted to electromagnetic waves. Experimentalists have shown they can cloak objects from surface water waves [1] and electron waves on the surface of metals (plasmons) [2]. Now, Nicolas Stenger at the Karlsruhe Institute of Technology in Germany and his colleagues have designed and tested a cloak that makes an object in a flexible medium invisible to elastic vibrational waves [3]; that is, the waves pass by the object as though it wasn’t there. The work, which is presented in Physical Review Letters, describes a cloaking device that is both more efficient and covers a wider bandwidth than any other existing cloak.

Theoretical and experimental work developing cloaks for electromagnetic waves has progressed impressively. Early experiments by physicists at Duke University [4] showed that the scattering of microwaves near a copper cylinder could be reduced if the cylinder was surrounded by a suitably structured cloak. More recently, Jensen Li and John Pendry [5] at Imperial College London introduced the idea of carpet cloaking, where the cloak is placed in front of a mirror to hide the existence of a protuberance that would otherwise be detected by reflected light. The designs of most cloaks are based on transformation optics—the mathematics describing how light waves bend around an object (see 16 November 2009 Trends)—and make use of composites made of two or more materials that have an inhomogeneous index of refraction. In practice, the cloaks are typically simplified versions of an “ideal” cloak, so as to facilitate fabrication.

Extending these ideas to the realm of waves in solids, Stenger et al. consider elastic waves moving in a thin membrane. For such waves, and under certain approximations, the important physical parameter is the Young’s modulus of the membrane, which determines the speed of the waves. One important fact utilized by Stenger et al. is that appropriate materials, with a ratio of $1000$ : $1$ in Young’s modulus, are available; such a ratio is highly advantageous in bending waves round obstacles and would be difficult, if not impossible, to achieve in the corresponding optical situation.

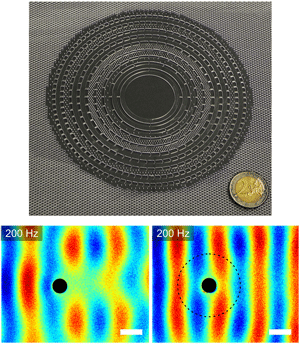
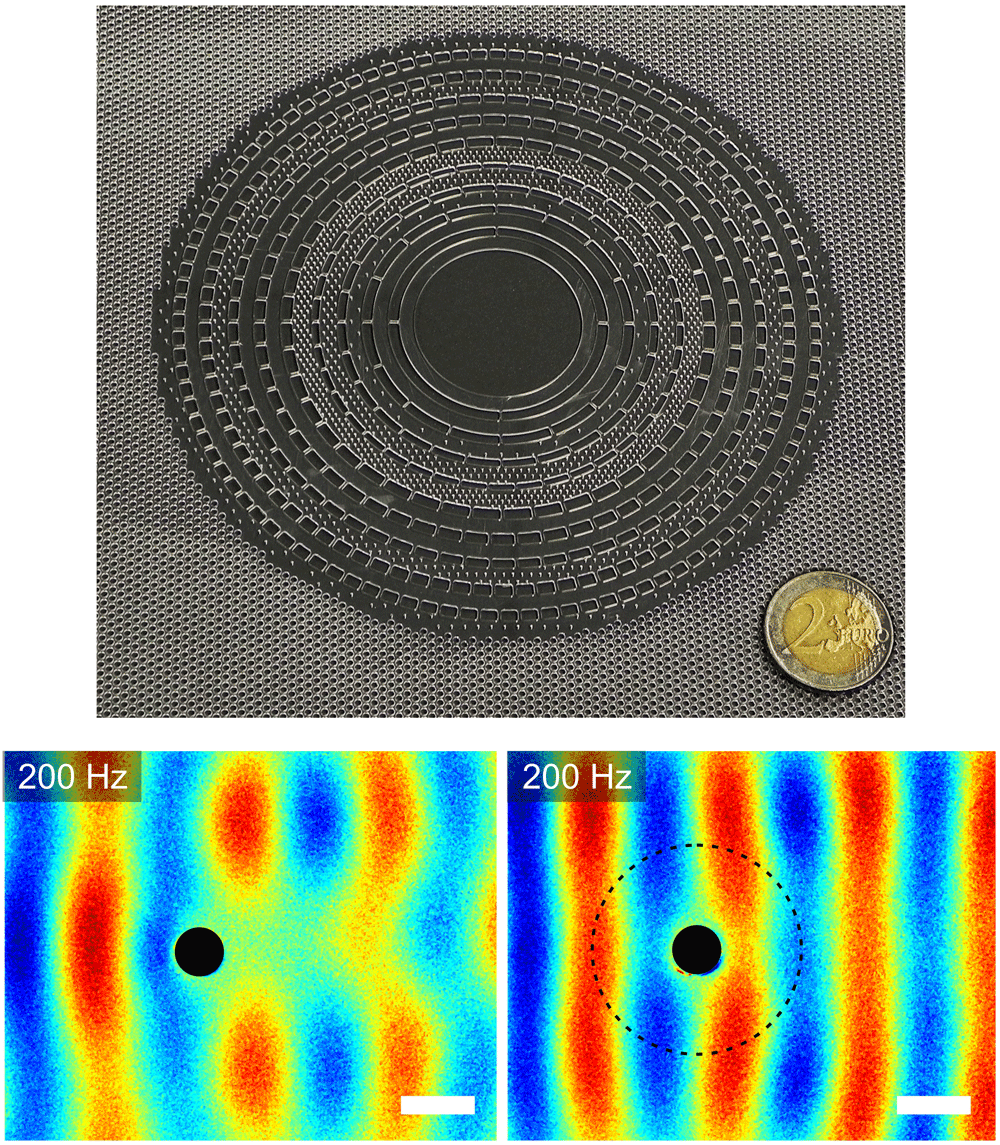
Stenger et al.’s cloak is based on a theoretical proposal [6] (coauthored by one of us) that adapted the ideas of transformation optics to the cloaking of elastic waves. This initial design of a cloaking ring consisted of ten rings and six different materials. Stenger et al. simplified this design with a composite structure consisting of only two materials with strongly contrasting Young’s moduli, and achieved the necessary spatial variation in the Young’s modulus by adjusting how much of each material they used. To guide their design, they modeled each composite ring of the structure numerically to achieve an effective Young’s modulus for a given composition ratio, and experimentally verified that this effective parameter was accurate. They then took a set of $20$ concentric rings, each with an adjustable composition ratio and thickness, and adjusted these $40$ parameters to achieve optimal cloaking using a so-called genetic algorithm, which uses a mechanism akin to natural selection to improve a design. They used these parameters to construct the physical cloak by drilling many small holes in a thin plate of the stiffer of the two materials (PVC, a common plastic), and filling the holes with the softer material (PDMS, a form of silicone). The entire cloak [Fig. 1(a)] is embedded in a thin, porous PVC plate.

Stenger et al. generated vibrations (at selected frequencies) in the thin plate using a loudspeaker placed at one side of the plate. They created absorbing boundary conditions at the other sides of the plate by lining them with soft foam, which acted like a perfectly matched layer. The pattern of waves passing over a rigid inclusion in the plate is markedly different with and without a cloak surrounding it: without the cloak, the wave fronts are broken up as they pass over the inclusion, like waves encountering a buoy; with the cloak, the waves seem to pass by undisturbed [Fig. 1(b)]. Stenger et al. find the cloak is most effective at a wave frequency of $200$ hertz ( $Hz$ ), and slowly deteriorates as the frequency is raised to $400 Hz$ (the highest frequency they tested). The bandwidth over which their cloaking device works—an octave in frequency—is impressive, considering that optical cloaks must only cover the visible spectrum from $400 nm$ to around $680 nm$ (a factor of $1.7$ in frequency).

In the supplementary material that accompanies their paper, Stenger et al. quantified the effectiveness of the cloak at different frequencies. At a fixed distance in the shadow region behind the inclusion they measured the average vibration amplitude for positions in the transverse direction. They then constructed the normalized variance of the vibration amplitude away from its mean value with the cloak present and with no cloak. In this analysis, at the $200 Hz$ frequency where the cloak is most effective, the cloak reduces the strength of vibrations in the shadow behind the inclusion by a factor of $8$ . A similar numerical analysis, interestingly, predicts the cloak will only attenuate the vibrations by a factor of $4$ . So far, only one other group has performed this type of analysis for another type of cloak: plasmonic carpet cloaks [2]. There the authors measured the bandwidth of a plasmonic carpet cloak and found a frequency ratio (highest frequency to lowest) of $1.38$ , while their figure for the effectiveness of cloaking was $3.7$ . It is thus clear that Stenger et al. have presented the clearest demonstration of effective cloaking in the literature to this point.

New research opportunities may result from the availability of elastic wave metamaterials. One example is the use of a simple elastic wave device consisting of three rows of clamped pins, which can provide an equivalent to a quantum mechanical effect called induced electromagnetic transparency (IET) [7]. IET occurs in atoms in an ultracold gas: the atoms normally absorb light in a particular frequency range, but the absorption can be blocked by a laser tuned to just the right frequency. Similarly, the three rows of pins in the device described in [7] can create just the right interference between elastic waves so that waves with nominally perfect transmission are completely attenuated. This type of elastic wave manipulation provides a new research area in which there will be many opportunities for developing striking wave effects and devices. Elastic waves offer materials parameters and fabrication possibilities which are not easily matched with other wave types, and thus provide an exciting test ground for new techniques to control waves in unprecedented ways for a whole range of demanding applications, such as cloaking, filtering, and ultraslow propagation. Such opportunities will enable cloaking to come out of the shadows.

References

M. Farhat, S. Enoch, S. Guenneau, and A. B. Movchan, Phys. Rev. Lett. 101, 134501 (2008)
J. Renger, M. Kadic, G. Dupont, S. S. Aćimović, S. Guenneau, R. Quidant, and S. Enoch, Opt. Express 18, 15757 (2010)
N. Stenger, M. Wilhelm, and M. Wegener, Phys. Rev. Lett. 108, 014301 (2012)
D. Schurig, J. J. Mock, B. J. Justice, S. A. Cummer, J. B. Pendry, A. F. Starr, and D. R. Smith, Science 314, 977 (2006)
J. Li and J. B. Pendry, Phys. Rev. Lett. 101, 203901 (2008)
M. Farhat, S. Guenneau, S. Enoch, and A. B. Movchan, Phys. Rev. B 79, 033102 (2009)
S. G. Haslinger, N. V. Movchan, A. B. Movchan, and R. C. McPhedran, Proc. R. Soc. London A 468, 76 (2012)

About the Authors

Ross McPhedran holds a personal chair in Electromagnetic Physics at the University of Sydney. He is well known internationally for his work on many aspects of the science of waves, including diffraction physics, composite materials, photonic band gap materials and photonic crystal fibers, metamaterials, multipole formulations, and elastodynamics.

Alexander Movchan holds a Chair of Applied Mathematics, and he is the Head of Department of Mathematical Sciences at the University of Liverpool. He is known for his work on asymptotic models of defects in solids and wave propagation and structured elastic media. He has more than 200 publications in this area of research.