Precision Measurement with Cold Atoms
The precise measurement of time and space, two of the most basic attributes of our universe, allows us to test some of the most fundamental aspects of physics, such as local Lorentz invariance, the gravitational redshift, and the universality of free fall, and allows us to look for temporal drifts of fundamental constants. In a more applied setting, the precise measurement of time and space allows us to measure inertial quantities—linear acceleration, rotation, gravity, and their gradients—that are critical to exploration and navigation both for civilian and defense applications.
Over the last two decades, light-pulse atom interferometry has been developed and applied to inertial measurements [1]. Writing in Physical Review Letters, Shau-Yu Lan at the University of California at Berkeley and colleagues employed a tip-tilt mirror to mitigate the Coriolis effect on an atom-light interferometer, caused by Earth’s rotation [2]. The development is significant because it enabled the group to demonstrate a cold-atom interferometer operating with the largest enclosed spacetime area to date. The sensitivity of measurements based on this kind of interferometer scales linearly with the enclosed area. As the authors discuss, the Coriolis effect has limited both the accuracy and precision of measurements of this kind.
Cold atoms provide universally available stable oscillators that can be applied to precision measurement. Atom-based technology revolutionized the measurement of time with the realization of the first atomic microwave clock in 1955 [3]. The principle of the measurement is straightforward: Write the phase of a countable microwave oscillator to a stable atomic oscillator. Let the countable oscillator and atomic oscillator evolve independently and compare their phases after a period of free evolution. If the countable oscillator has drifted in frequency during the free evolution time, the drift will manifest as a phase shift that can be measured by an atom interferometer. The interferometer output is converted to an error signal and fed back to stabilize the countable oscillator. The cycles of the stabilized countable oscillator are the clock output. Such technology allows the realization of clocks that are stable to better than part in in a second measurement. The highest precision microwave clocks isolate the stable atomic oscillators from the environment by employing atoms in free fall that are derived from an atomic fountain.
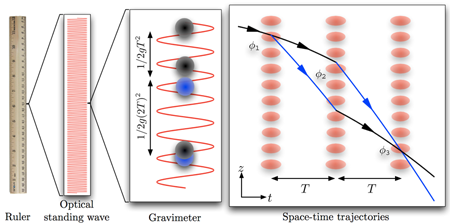
Inertial quantities, broadly termed accelerations (but including gravity and rotations), can be measured by similar cold-atom technology. Acceleration of the lab frame that carries the probing lasers is measured with respect to an inertial frame provided by freely falling cold-atom test masses. If the lab frame accelerates while the atoms are in free fall, the location of the atoms will change, as measured by a ruler tied to the accelerating frame. This is the principle of cold-atom inertial measurement. In the work reported by Lan et al., the ruler is provided by a standing wave formed from two counterpropagating lasers. An example of such measurement similar to either the lower path or upper path interferometer in the paper by Lan et al. is given in Fig. 1.
The phase of the laser ruler exhibits a strong spatial phase dependence, evolving by every half optical wavelength. Space is now encoded as phase, and the phase difference of the Bragg beams provides the ticks on the ruler. Again, it is an interferometric comparison of laser phase and atomic phase after a free evolution time that forms the basis of the measurement. A relative phase shift of lasers and freely falling atoms manifests as a population difference in the two output ports of the atom interferometer. The laser ruler (Bragg beams) provides the beam splitters and mirrors. The relative population in the output ports encodes the phase shift and ultimately allows a measurement of the acceleration.
The sensitivity of light-atom interferometric measurements is limited fundamentally by the flux of the atomic source, the quantum noise that characterizes the atomic source, the beam splitting angle (momentum imparted in the Bragg beam splitting process), and the free evolution or free fall time. All four fundamental parameters are worth consideration. Unless we find a new route to cool atoms to sub microkelvin temperatures, it would seem unlikely that we will see orders of magnitude improvement in the flux of cold-atom sources. Investigating alternative cooling mechanisms is an active field of research [4]. Although squeezing the quantum noise on an atomic source is difficult and must be coupled with low losses and high quantum efficiency detection if it is to be useful for metrology, there have been some exciting advances in recent years, at least for small samples of atoms [5,6]. The challenge is to squeeze a large number of atoms so the result is significant to metrology.
For Earth-based measurements, the only way to very substantially increase the interrogation time is to use a trapped test mass rather than a freely falling test mass. Trapped masses are strongly coupled to the environment for the entire duration of the measurement, and it is unclear whether this is a viable route to vastly improved sensitivity. The sensitivity of atom interferometers to inertial quantities increases linearly with the enclosed spacetime area, that is, it increases with the momentum imparted in the beam splitting process. This is a promising path forward to significantly improved precision, and it is in this context that the paper by Lan et al. represents a significant step forward.
Large momentum transfer (LMT) beam splitters have been developed and investigated by several groups, but in all cases, the contrast of the fringes that provide the phase measurement decreases rapidly with the momentum transferred in the process and decreases rapidly with the free fall time [7–11]. The work of Lan et al. makes it clear that the Coriolis effect due to Earth’s rotation is a major contributor to the loss of fringe contrast that limits the efficacy of LMT beam splitters. The tip-tilt mirror they have employed improves the contrast obtained with a ten-photon beam splitter and decreases the systematic shift associated with the Coriolis effect.
The principle of operation of the tip-tilt mirror is as follows: The moving standing wave that forms the ruler is aligned vertically in the direction of local gravity. The atoms are released and subjected to a series of light pulses that act as the beam splitters and mirrors that are the basis of the atom interferometer. In the ideal situation, the light pulses would all propagate along the same vertical axis. Rotation of the lab frame due to Earth’s rotation during the free fall time of the atoms means that the axis defined by the optical ruler rotates in the freely falling atom frame.
This has two effects: There is a systematic offset in the measurement because the atoms free fall trajectory and the axis of the ruler do not coincide throughout the measurement. In addition, there is a loss of fringe contrast and a concomitant loss of precision because the atomic wave packets do not overlap, or are not perfectly mode matched at the output beam splitter. The fix employed by Lan et al. to counteract Earth’s rotation is to tilt the retroreflection mirror that provides the counterpropagating beam in the optical ruler. The momentum transferred in the mirror and beam splitter operations, as seen from the atom’s inertial frame, is now in a constant direction, and is parallel to the direction of gravity at the initial release point, despite Earth’s rotation.
Lan et al. also observe a loss of fringe contrast with increasing free fall time and attribute it to wave front distortion in the optical ruler. This effect has been observed in every LMT experiment performed to date [7–11]. It would seem reasonable that the requirement on wave-front flatness would be alleviated by the very narrow divergence provided by atom lasers sourced from Bose condensed samples. The authors also note in their paper that an increase in wave-packet size (coherence length) provided by Bose condensed sources would also mitigate the loss of fringe contrast due to the Coriolis effect but would not remove the systematic shift. A promising path forward may well be to employ the tip-tilt mirror described by Lan et al. with Bose condensed or atom laser sources [11,12].
References
- A. D. Cronin, J. Schmiedmayer, and D. E. Pritchard, Rev. Mod. Phys. 81, 1051 (2009)
- S-Y. Lan, P-C. Kuan, B. Estey, P. Haslinger, and H. Müller, Phys. Rev. Lett. 108, 090402 (2012)
- L. Essen and J. V. L. Parry, Nature 176, 280 (1955)
- S. Magkiriadou, D. Patterson, T. Nicolas, and J. M. Doyle, New J. Phys. 13, 023012 (2011)
- M. F. Riedel, P. Böhi, Y. Li, T. W. Hänsch, A. Sinatra, and P. Treutlein, Nature 464, 1170 (2010)
- C. Gross, T. Zibold, E. Nicklas, J. Estève, and M. K. Oberthaler, Nature, 464,1165 (2010)
- H. Müller, S. W. Chiow, Q. Long, S. Herrmann, and S. Chu, Phys. Rev. Lett. 100, 180405 (2008)
- H. Müller, S. W. Chiow, S. Herrmann, and S. Chu, Phys. Rev. Lett. 102, 240403 (2009)
- P. Cladé, S. Guellati-Khelifa, F. Nez, and F. Biraben, Phys. Rev. Lett. 102, 240402 (2009)
- S.-W. Chiow, T. Kovachy, H.-C. Chien, and M. A. Kasevich, Phys. Rev. Lett. 107,130403 (2011)
- J. E. Debs, P. A. Altin, T. H. Barter, D. Döring, G. R. Dennis, G. McDonald, R. P. Anderson, J. D. Close, and N. P. Robins, Phys. Rev. A 84, 033610 (2011)
- S. Szigeti, J. E. Debs, J. J. Hope, N. P. Robins, and J. D. Close, New J. Phys. 14, 023009 (2012)
- J. E. Debs, Ph.D. Thesis, The Australian National University (2012)