New Twist in Chiral Magnets

Catherine Pappas

Viewpoint

New Twist in Chiral Magnets

Delft University of Technology, Faculty of Applied Sciences, Mekelweg 15, 2629 JB Delft, The Netherlands

March 5, 2012• Physics 5, 28

A new state of matter involving twisting magnetic moments has been observed for the first time, possibly opening up novel applications in information technology.

Figure caption — **Figure 1:** The magnetic moments in ${Cr}_{1 / 3} {NbS}_{2}$ rotate around in a left-handed helix (top). When an external magnetic field is applied (bottom), a chiral magnetic soliton lattice appears, in which the helical shape is stretched out wherever the moments and field are aligned.

Chiral magnets have fascinating properties that could make them important ingredients for future data storage and other information technology applications. The internal magnetic fields in these magnets are typically spirals or swirls, but new experiments with the chiral magnet, ${Cr}_{1 / 3} {NbS}_{2}$ , have uncovered a never-before-seen type of magnetic twisting called a chiral magnetic soliton lattice. Yoshihiko Togawa of Osaka Prefecture University in Japan and his colleagues—reporting in Physical Review Letters—showed that they could control the shape of this lattice with an external magnetic field [1]. This capability could provide a new kind of control switch in future spintronic devices.

Chirality is commonly found in nature, from particle physics to molecular chemistry. It is characterized by a reflection asymmetry that we are most familiar with in terms of our left hand being the mirror opposite of our right hand. When this kind of handedness appears in the structure of atoms in a solid, it affects the way that the magnetic moments of unpaired electrons organize themselves through the relativistic spin-orbit Dzyaloshinskii-Moriya (DM) interactions. These antisymmetric interactions have the form $- D \cdot {\vec{S}}_{i} \times {\vec{S}}_{j}$ , where $D$ is the strength of the DM coupling and ${\vec{S}}_{i}$ and ${\vec{S}}_{j}$ are the spins of different electrons. In a symmetric structure, these interactions cancel out, but in a chiral lattice they do not. The DM interactions favor a screwlike arrangement of the magnetic moments, but they must compete with ferromagnetic exchange, which tries to align all the magnetic moments in the same direction. The result is a helical magnetic arrangement with a winding period of several tens of nanometers, which is much longer than the lattice constant. Therefore, even though the chiral properties depend on the symmetry of the lattice, they can be understood and manipulated at the larger nanoscale, and even the mesoscopic level, independently of the structural details.

Chiral magnets—in particular the prototypical chiral magnet manganese silicide ( $MnSi$ )—have attracted interest over the last few years due to their exciting properties. Potentially, they might one day reach a degree of functionality similar to that of chiral liquid crystals. This speculation is based on some strong parallels between chiral magnets and liquid crystals. Both materials have helical structures, and they both contain extremely stable excitations called solitons. Solitons are nonlinear excitations that behave like particles, maintaining their shape and energy as they propagate, as exemplified by tsunamis that travel across entire oceans. In chiral magnets, solitons take the form of one-dimensional kinks or two-dimensional vortices called skyrmions. These solitonic excitations are stabilized by temperature and magnetic fields [2]. They are extremely robust and can be manipulated by electric currents [3] or even condense to form a regular lattice, such as the lattice of skyrmions found in MnSi and other related systems [4].

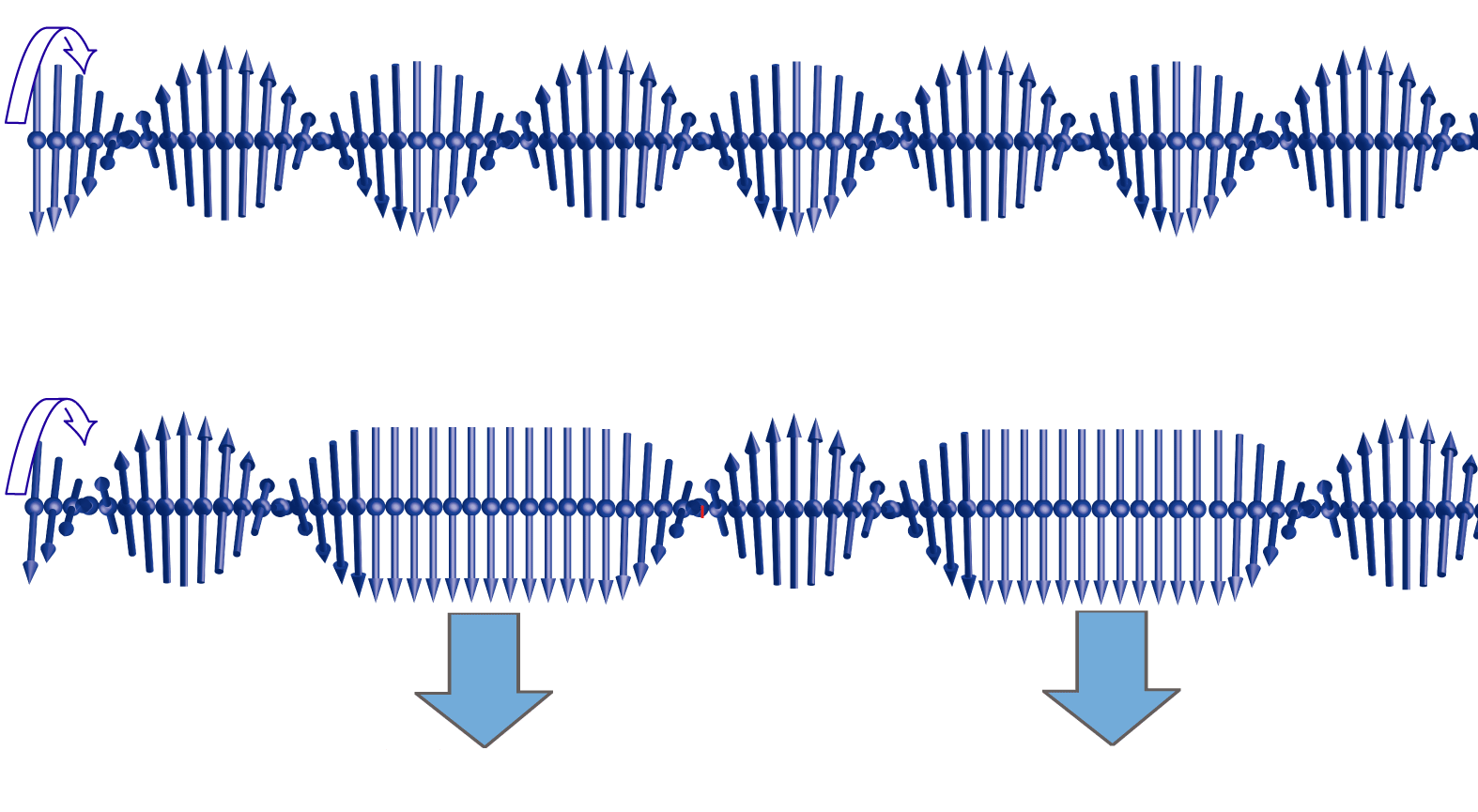
$MnSi$ is cubic and nearly isotropic, but the situation is very different for hexagonal ${Cr}_{1 / 3} {NbS}_{2}$ . Below $127$ K, ${Cr}_{1 / 3} {NbS}_{2}$ takes the form of a left-handed helimagnet, whose magnetic moments spiral around the lattice’s principle axis with a pitch of $48$ nanometers. It is possible to apply a magnetic field either parallel or perpendicular to the helical axis—thus providing an additional “control switch” that does not exist in the highly symmetric cubic chiral magnets such as $MnSi$ . Togawa and co-workers take advantage of this switch by applying a magnetic field perpendicular to the helical axis of a thin slab of ${Cr}_{1 / 3} {NbS}_{2}$ . Using electron diffraction and Lorentz microscopy, they observe an increase in the distance it takes for the magnetic moments to complete a full spiral. Essentially, the helix stretches out, but only where the moments are aligned with the external magnetic field (see Fig. 1). These “kinks” define a chiral magnetic soliton lattice. The researchers found that they could tune the shape of this lattice by varying the strength of the magnetic field.

Theory had anticipated that chiral magnetic soliton lattices would exist and that they would exhibit a variety of interesting functions. Togawa et al.’s work provides the very first direct observation of this new state of matter. These pioneering experiments show that it is possible to generate and tailor such structures by adequate use of the lattice symmetry and the applied magnetic field. This opens up new perspectives in nanomagnetism and spintronics applications. As the authors point out, these chiral magnetic features function as a tunable effective potential for itinerant electron spins, which are the current-carriers in spintronic devices. The high stability, robustness, and tunability of soliton kinks—and similar textures like skyrmions—open the door to a fascinating functionality at the nanoscale. They could be the building blocks of macroscopic nanoscaled magnetic structures and the three-dimensional memories of the future [5].

References

Y. Togawa, T. Koyama, K. Takayanagi, S. Mori, Y. Kousaka, J. Akimitsu, S. Nishihara, K. Inoue, A. S. Ovchinnikov, and J. Kishine, Phys. Rev. Lett. 108, 107202 (2012)
U. K. Rößler, A. N. Bogdanov, and C. Pfleiderer, Nature 442, 797 (2006)
F. Jonietz et al., Science 330, 1648 (2010)
X. Z. Yu, Y. Onose, N. Kanazawa, J. H. Park, J. H. Han, Y. Matsui, N. Nagaosa, and Y. Tokura, Nature 465, 901 (2010)
S. S. P. Parkin, M. Hayashi, and L. Thomas, Science 320, 190 (2008)

About the Author

Catherine Pappas is a condensed-matter experimentalist with interests in chiral, frustrated, and disordered magnetism. Her expertise is in the fields of polarized neutron scattering and instrumentation. She received her Ph.D. in 1984 from the University Paris-Sud in Orsay, France, and then moved to Berlin, first to the Free University and later to the Hahn-Meitner Institute, nowadays Helmholtz Zentrum Berlin. Since 2009 she has been a professor at the Faculty of Applied Sciences, Delft University of Technology, The Netherlands.