Ultrafast Phase Control in Oxide Thin Films
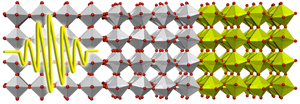
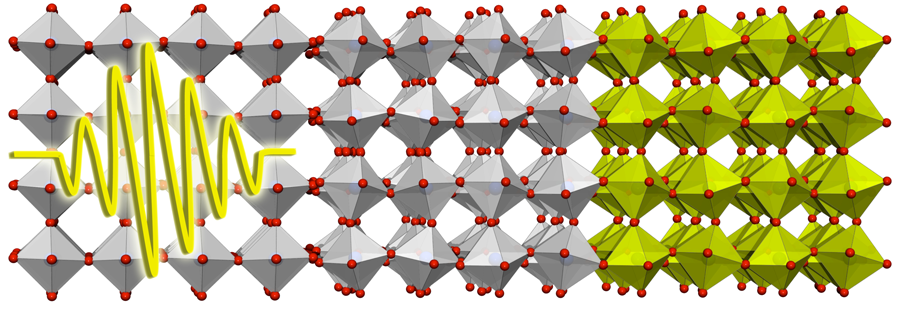
Complex oxides have complicated phase diagrams as a function of temperature, doping, pressure, or applied external fields. In a strained film, the interplay between the electrons and the lattice often leads to the stabilization of an ordered state different from that found in bulk in the same material. This issue is particularly important in the versatile oxide heterostructures, where one may find electronic phases occurring at interfaces that are distinct from electronic phases in bulk. Both strain and external pressure can modify the lattice of an oxide. An alternative is to optically excite particular vibrational modes in the material. Now, reporting in Physical Review Letters, Andrea Caviglia at the University of Hamburg, Germany, and co-workers [1] have shown that a long-lived five orders of magnitude increase of the conductivity of a nickelate ( NdNiO3) can be produced by optically exciting a vibrational mode on the substrate. The propagation of a vibrational mode from a substrate to a thin film grown on it (see Fig. 1) potentially opens up a new way to explore and manipulate the electronic reconstruction that takes place at the interfaces between different oxides.
Celebrated examples of complex oxides include the high-temperature superconducting cuprates, colossal magnetoresistance manganites, ferroelectrics, and multiferroics (materials that combine two or more ferroic orders). This diversity of properties and functionalities arises in systems with a complicated energy landscape, with small energy barriers between different local minima, due to the intricate interplay among spin, charge, orbital, and lattice degrees of freedom. This electronic softness may lead to phase separation [2] and phase coexistence [3]. Phase transitions can then be produced by inducing small changes in the system parameters. For instance, a metal to insulator transition can take place if the ratio between the kinetic energy of the carriers and localizing interactions is reduced.
In the last decade or so, the interest in oxides has been extraordinarily boosted by the technical possibility of growing very high quality oxide heterostructures where ultrathin layers (down to atomic scale) with different chemical compositions can be combined. In these heterostructures, phases distinct from those expected in bulk have been observed at the interfaces: one of the most studied examples is that of the metallic interface between two insulators LaAlO3 and SrTiO3, from which electronic devices have been nanopatterned by means of the field effect. This reminds us of the well-known two-dimensional electron gases in semiconductor heterostructures, but interactions in the oxides make these electron gases even more interesting with the appearance of superconductivity or magnetism in certain cases [4]. Good quality oxide interfaces also allow the exploration of the interaction between ordered states that are usually mutually exclusive, e.g., ferromagnetism and superconductivity, by growing convenient heterostructures. And it is possible to compensate for the scarcity of bulk multiferroic materials by forcing alternate layers of ferromagnets and ferroelectrics to couple. With so many known oxides to choose from, recent literature abounds with interesting examples [5].
Most of these oxides are ternary compounds (chemical composition ABO3, where B is a transition metal) with a perovskite structure. In perovskites, the oxygen atoms form corner-sharing octahedra around the B atoms, and the A atoms sit in the spaces in between. The ideal perovskite structure would have cubic symmetry, but in practice there are many distortions the lattice suffers: the octahedra rotate and tilt to adapt to the atomic sizes and can also undergo different cooperative distortions sometimes associated with charge disproportionation and orbital modulations. Different vibrational modes (phonons) thus occur in the perovskites. The rotations and deformations of the oxygen octahedra modify the overlap between orbitals in neighboring atoms, affecting the kinetic energy of the carriers in the system and its ratio with the localizing interactions. With this picture in mind, one can easily see that manipulating the lattice can sometimes be an effective means to stabilize different ground states.
The lattice distortions occurring in bulk are modified when thin films are grown on a substrate with a different lattice parameter [5]. This corresponds to applying a biaxial pressure where the in-plane lattice parameters of the thin film are expanded or contracted to the atomic spacing imposed by the substrate. If the substrate is electrostrictive, its shape can be altered by applying an electric field, providing us with a switch to modify the thin-film ground state. Another switch can be realized by exciting different modes of vibration (phonons) using resonant radiation: By applying very short (a few femtosecond long) pulses, it is possible to produce a transient electronic response (up to 1 nanosecond long). This technique has been successfully applied before to dramatically decrease the resistance of a nominally insulating manganite [6] and to induce superconductivity in a stripe-ordered cuprate [7]. In these cases, time-resolved measurements could provide valuable information about the electronic phases involved.
Nickelates are another example of oxide perovskites where the electronic degrees of freedom and the lattice are coupled. In particular, NdNiO3 is an antiferromagnetic insulator below 200K; above this temperature, it becomes metallic with a sharp drop in resistivity of many orders of magnitude. The nature of this metal-to-insulator transition is still under debate. So far this transition has been explored with static experiments involving strain, pressure, or electric fields. Caviglia et al. [1] have produced the transition in a thin film of NdNiO3 grown on another oxide perovskite ( LaAlO3) by optically exciting a vibrational mode, not of the nickelate but of the substrate. The transient modification of the substrate lattice produces an ultrafast change of the strain on the insulating nickelate, which becomes metallic in less than 1 picosecond and survives in that state for more than 1 nanosecond. This fast charge dynamics has also been found in manganites and cuprates.
Similar experiments could, in principle, be done on many other oxide thin films and heterostructures. For instance, we could try to modify the orbital pattern observed in an interface between a manganite and a cuprate where superconductivity is suppressed [8] or affect the magnetoelectric coupling between ferromagnetic and ferroelectric layers in composite multiferroics [9]. Studying the dynamical response to changes in the lattice can give us a clue to the role of the electron-phonon interaction in the new phases arising at interfaces while allowing us to explore the possibilities of fast electronic phase switching for applications. Oxide thin films and heterostructures may still be full of surprises.
References
- A. D. Caviglia, R. Scherwitzl, P. Popovich, W. Hu, H. Bromberger, R. Singla, M. Mitrano, M. C. Hoffmann, S. Kaiser, P. Zubko, S. Gariglio, J-M. Triscone, M. Först, and A. Cavalleri, Phys. Rev. Lett. 108, 136801 (2012)
- E. Dagotto, Science 309, 257 (2005)
- G. C. Milward, M. J. Calderón, and P. B. Littlewood, Nature 433, 607 (2005)
- J. Mannhart, D. H. A. Blank, H. Y. Hwang, A. J. Millis, and J.-M. Triscone, MRS Bulletin 33, 1027 (2008)
- P. Zubko, S. Gariglio, M. Gabay, P. Ghosez, and J.-M. Triscone, Annu. Rev. Condens. Mat. Phys. 2, 141 (2011)
- M. Rini, R. Tobey, N. Dean, J. Itatani, Y. Tomioka, Y. Tokura, R. W. Schoenlein, and A. Cavalleri, Nature 449, 72 (2007)
- D. Fausti, R. I. Tobey, N. Dean, S. Kaiser, A. Dienst, M. C. Hoffmann, S. Pyon, T. Takayama, H. Takagi, and A. Cavalleri, Science 331, 189 (2011)
- J. Chakhalian, J. W. Freeland, H.-U. Habermeier, G. Cristiani, G. Khaliullin, M. van Veenendaal, and B. Keimer, Science 318, 1114 (2007)
- J. Ma, J. Hu, Z. Li, and C.-W. Nan, Adv. Mater. 23, 1062 (2011)