Rydberg Atoms Jump in Bunches
When an atom is excited to a high-lying electronic state, virtually all of its properties become vastly exaggerated. The size of these so-called Rydberg atoms scales quadratically with the principal quantum number , while the electron motion slows down by the same fraction, drastically increasing the time it takes for the atom to radiatively decay. As a result, Rydberg atoms feel a strong van der Waals attraction or repulsion to one another that scales as ; a tenfold increase of the atom’s excitation level therefore enhances the potential energy between two Rydberg atoms by orders of magnitudes. These strong interactions shift the energy levels of the atoms and are sufficient to affect optical Rydberg excitation over distances as large as several micrometers—an effect [1] that forms the basis for a number of fascinating phenomena and promising applications. In a theoretical paper appearing in Physical Review Letters, Tony Lee at the California Institute of Technology, Pasadena, and his colleagues now show that this effect, which is known to alter the way an ensemble of Rydberg atoms coherently interacts with light [1], can also dramatically change how such atoms radiate [2].
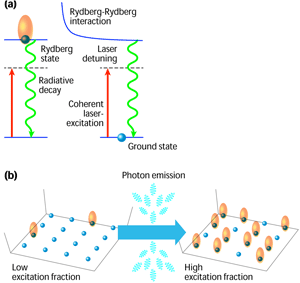
While highly excited atoms have long been of interest since the early days of atomic physics, the advent of techniques to trap and cool atoms down to a few microkelvin or less has given birth to a subfield of Rydberg atom physics [3]. At ultralow temperatures, Rydberg atoms are a model building block for making a neutral-atom quantum computer [1]: the atoms have long radiative lifetimes (good for preserving quantum information) and the interactions between atoms are strong (good for manipulating information rapidly). This capability was recently demonstrated experimentally for two atoms [4] (see 8 January 2010 Synopsis). Systems containing many Rydberg atoms act as an effective spin ensemble, where the ground and Rydberg state of each atom represents the down and up states, respectively, of a fictitious spin. The local dynamics of such spins can be controlled by the intensity and frequency of a laser tuned to the excitation energy of the Rydberg atom, while coupling between spins is mediated by the long-range interactions between Rydberg atoms [Fig. 1(a)]. These ensembles can be used as quantum simulators of exotic Hamiltonians [5], for engineering long-range interactions in Bose-Einstein condensates [6] or to prepare entangled, i.e., quantum correlated, many-body states [7,8].
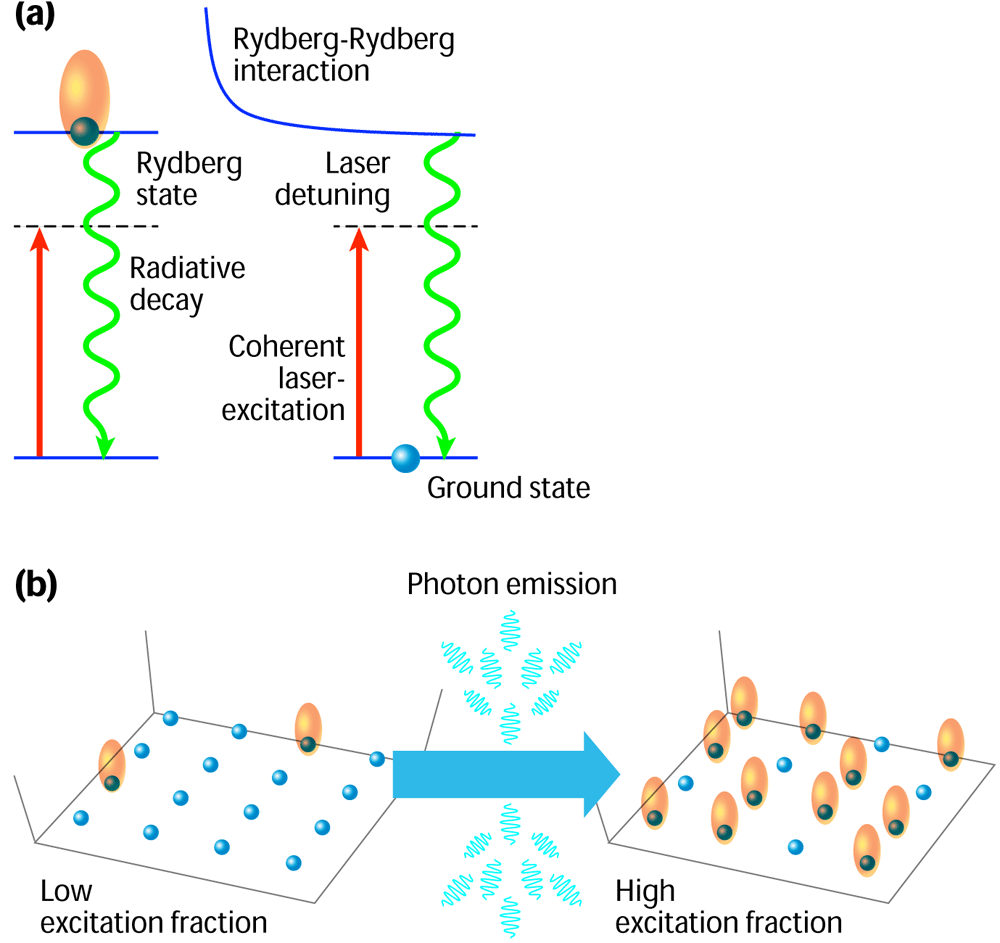
Most of these schemes rely on the long radiative lifetime of highly excited atoms and therefore can typically operate no longer than a few microseconds. On the other hand, Lee et al. turn this limitation into a feature. Investigating the excitation dynamics of cold Rydberg gases over much longer times, they have uncovered a connection between entanglement among multiple Rydberg atoms and the way these excited states lose energy, which leads them to an unexpected result. If they start with a small fraction of excited atoms, the radiative decay of one atom tends to increase the probability for finding the remaining atoms in a Rydberg state. This enhances the subsequent decay of other atoms and culminates in an avalanchelike population of a large fraction of excited states [Fig. 1(b)]. This behavior comes as a surprise, as one might reasonably think that excited-state decay decreases, rather than increases, the number of excited atoms.
Lee et al. explain this seemingly counterintuitive finding using the notion of so-called quantum jumps: photons emitted from an atom during its spontaneous decay can, in principle, be measured (by an external observer) such that the atom is continuously monitored by its environment. Each emission, consequently, abruptly projects the respective atom into its ground state. For two atoms, this quantum jump projects the doubly excited state containing two Rydberg excitations to the singly excited state with one excitation, and so on. Without interactions, the atoms decay independently of each other and the corresponding projection can only decrease the fraction of excited atoms, as expected. However, this restriction no longer holds in the presence of entanglement, i.e., with the atoms interacting. Consider, for example, a simple entangled state, which contains mostly the two-atom ground state plus a small amplitude of the doubly excited, two-atom Rydberg state, corresponding to a probability for finding a particular atom in the excited state. Once an atom decays, the other atom has to be in the Rydberg state, which increases its excitation probability to unity and thereby greatly enhances its subsequent decay. Lee et al. show that such a population inversion and the resulting collective decay can indeed be observed for a properly chosen intensity and frequency of the excitation laser.
This simple configuration illustrates the sometimes weird effects that arise from quantum correlations. It also captures the essential physics behind the dynamics of larger systems driven by the coherent build-up of many-body entanglement and incoherent quantum jumps. Lee et al. describe this more complex situation by approximating the Rydberg-Rydberg atom interaction by constant level shifts that are identical for all Rydberg atom pairs, irrespective of their mutual distances. Their analysis starts from a mean-field treatment, which neglects atom-atom correlations and instead mimics atomic interactions by an average potential, related to the mean number of Rydberg excitations in the sample. Using this approximation, the many-body system can be described by a single set of optical Bloch equations, plus a nonlinearity arising from the Rydberg-Rydberg interactions. This nonlinearity makes the steady state of these equations bistable for certain laser parameters, meaning the system can eventually settle into one of two stable fixed-points. Lee et al. find that they correspond to two distinct states—one with a low and one with a high fraction of Rydberg excitations—and are closely linked to the collective dynamics of the ensemble.
Such bistabilities are common in classical nonlinear systems, which are known to switch spontaneously between two stable points upon stochastic driving. Here, Lee et al. discover similar behavior, but with the all-important difference that the switches are nonclassical in nature and induced by the interplay of quantum entanglement and spontaneous single-atom decay. They demonstrate this point via numerical simulations of the fully correlated quantum dynamics of small atomic ensembles. Their results show that, under conditions of classical bistability, the Rydberg atom number indeed jumps between two distinct values, which correspond precisely to the two stable fixed points of the mean-field model.
The close agreement between the mean-field prediction and the exact quantum dynamics is surprising. On the one hand, the mean-field approach neglects any atomic correlations, producing a fictitious nonlinearity that gives rise to the observed bistability. On the other hand, the collective quantum jumps rest entirely on quantum correlations that emerge from the linear time-evolution of interacting atoms.
However, mean-field approximations are known to work best for the infinitely ranged interactions used by Lee et al. Their success may well motivate future work to elucidate the importance of more realistic interaction potentials or establish links between classical bistabilities and collective quantum jumps in other systems, such as cavity arrays [9].
Related work [10] has suggested that collective quantum jumps of Rydberg atoms could be a source of correlated, nonclassical light—a core objective of quantum optics research. In this context, the authors’ findings will likely foster new ideas for current efforts to utilize cold Rydberg gases for deterministic few-photon entanglement [8,11] and as highly nonlinear optical media [12]. The constructive interplay between coherent and—often disregarded—dissipative processes points up interesting new directions for the still emerging field of cold Rydberg atom physics.
References
- D. Jaksch et al., Phys. Rev. Lett. 85, 2208 (2000); M. D. Lukin et al., 87, 037901 (2001)
- T. E. Lee, H. Häffner, and M. C. Cross, Phys. Rev. Lett. 108, 023602 (2012)
- M. Saffman, T. G. Walker, and K. Mølmer, Rev. Mod. Phys. 82, 2313 (2010); D. Comparat and P. Pillet, J. Opt. Soc. Am. B 27, A208 (2010); T. Pohl, C. S. Adams, and H. R. Sadeghpour, J. Phys. B 44, 180201 (2011)
- T. Wilk et al., Phys. Rev. Lett. 104, 010502 (2010); L. Isenhower et al., 104, 010503 (2010)
- H. Weimer et al., Nature Phys. 6, 382 (2010)
- N. Henkel, R. Nath, and T. Pohl, Phys. Rev. Lett. 104, 195302 (2010); F. Cinti et al., 105, 135301 (2010); F. Maucher et al., 106, 170401 (2011)
- B. Olmos, R. González-Férez, and I. Lesanovsky, Phys. Rev. Lett. 103, 185302 (2009)
- T. Pohl, E. Demler, and M. D. Lukin, Phys. Rev. Lett. 104, 043002 (2010)
- A. D. Greentree, C. Tahan, J. H. Cole, and L. C. L. Hollenberg, Nature Phys. 2, 856 (2006)
- J. D. Pritchard, C. S. Adams, and K. Mølmer, arXiv:1108.5165
- I Friedler, D. Petrosyan, M. Fleischhauer, and G. Kurizki, Phys. Rev. A 72, 043803 (2005); A. V. Gorshkov et al., Phys. Rev. Lett. 107, 133602 (2011)
- J. D. Pritchard et al., Phys. Rev. Lett. 105, 193603 (2010); D. Petrosyan, J. Otterbach, and M. Fleischhauer, 107, 213601 (2011); S. Sevinçli, N. Henkel, C. Ates, and T. Pohl, 107, 153001 (2011)