Electrons Weigh in on Ferroelectricity

Matthew Dawber

Viewpoint

Electrons Weigh in on Ferroelectricity

Department of Physics and Astronomy, Stony Brook University, Stony Brook, NY 11794-3800, USA

June 4, 2012• Physics 5, 63

New experiments on an organic ferroelectric verify that its electric polarization is driven primarily by an electron shift, rather than the ion shift that characterizes most other ferroelectrics.

Figure caption — **Figure 1:** Schematics illustrating the contrasting role of electronic ferroelectricity in ${BaTiO}_{3}$ and TTF-CA. (a) The cubic unit cell of ${BaTiO}_{3}$ is shown with $Ti$ in green, $Ba$ in blue, and $O$ in red. Some of the $2 p$ electron orbitals for the oxygen ions are drawn schematically in light blue. (b) Below $120^{\circ} C$ , the $Ti$ ion shifts upwards relative to the other ions, creating a dipole, ${\vec{p}}_{ion}$ . The electronic weight in the oxygen $2 p$ orbitals also shifts but, in this case, downwards, resulting in an additional electronic polarization, ${\vec{p}}_{ele}$ . (c) The TTF-CA crystal structure is composed of alternating stacks of TTF and CA molecules. In between, the hybridized electron orbitals are represented in light blue. (d) Below $81 K$ , the TTF molecules donate an electron to nearest neighboring CA molecule, and at the same time, shift upwards, producing an ionic polarization. A corresponding upward shift in the electronic weight of the hybridized orbitals creates a strong electronic dipole that points in the opposite direction to the ionic one.

If you opened up a solid-state physics textbook and read the chapter on ferroelectricity, you would be forgiven for thinking that the permanent electric polarization in ferroelectric materials is driven purely by relative shifts of ions within the structure. In reality, this polarization is partially due to a redistribution of electrons, as demonstrated in several studies over the last two decades. The extreme case, in which the ferroelectricity is dominated by displacement of the electronic weight, has been hinted at in theory but never experimentally verified until now. Kensuke Kobayashi from the High Energy Accelerator Research Organization (KEK) in Tsukuba, Japan, and colleagues performed detailed electric and x-ray measurements on an organic ferroelectric, as described in Physical Review Letters [1]. The results show that the electronic polarization is $20$ times the ionic polarization and that the two point in opposite directions. Ferroelectrics that have predominantly electronic polarization like this may exhibit new and unusual relationships between their polarization and their mechanical and/or magnetic properties.

Ferroelectrics are characterized by a spontaneous polarization (analogous to the spontaneous magnetization in ferromagnets), which occurs when the atoms within the material are arranged in a noncentrosymmetric structure. The polarization can be switched from one direction to another by the application of a sufficiently strong electric field, but once this is done the polarization will remain in that direction until an equally strong field is applied in the opposite direction. This property makes these materials very attractive as nonvolatile memories in electronic devices. Ferroelectrics also have a coupling between strain and polarization, making them good piezoelectrics, and sometimes have a coupling between magnetic order and polarization, which in the last decade has driven an intense research effort into multifunctional materials called multiferroics.

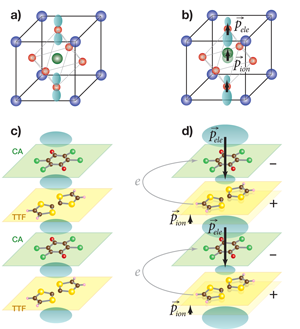
When first discussing ferroelectricity, the typical example presented is barium titanate ( ${BaTiO}_{3}$ ). Like many other ferroelectrics, this material has a perovskite structure (see top of Fig. 1). Above $120^{\circ} C$ , barium titanate is cubic, with one titanium in the center of the unit cell, a barium at each corner, and an oxygen on each face of the cube. If each atom were fully ionized, the bariums would be $2 +$ ions, the titanium would be a $4 +$ ion and the oxygens would each have a charge of $2 -$ . The combination of ${Ba}^{2 +}$ and $O^{2 -}$ ions act as a virtual ion of charge $4 -$ at the same position that is occupied by the ${Ti}^{4 +}$ ion, so the crystal is both neutral and nonpolar under these conditions. However, if barium titanate is cooled below $120^{\circ} C$ , a phase transition occurs, in which the unit cell elongates in one direction, causing the titanium ion to occupy an off-center position with respect to the virtual ion defined by the oxygen-barium cage. This ion shift leads to an electric dipole moment in the unit cell, and the sum of these dipoles gives an overall polarization to the crystal.

The positions of the ions can be measured using either x-ray or neutron diffraction, or calculated from first principles. With those ionic positions in hand, we might think we could calculate the dipole moment $\vec{p}$ of a unit cell using our freshman physics formula: $\vec{p} = Z Δ \vec{u}$ , where $Z$ is the charge of the ions and $Δ \vec{u}$ is their relative displacement from their nonpolar positions. But the sum over these dipoles underestimates the overall polarization, the true value of which can be determined experimentally from electrical measurements or calculated from the modern Berry-phase theory of polarization [2]. The reason for this discrepancy is a shift of the electronic weight around the titanium ion and the oxygen ions that lie along the dipole direction. Effectively, the $2 p$ electron orbitals belonging to the oxygens move off-center in the direction opposite that of the titanium ion (see Fig. 1), creating additional polarization in the same direction as that generated by the titanium displacement [3].

This shift of the electronic weight in the crystal is referred to as electronic ferroelectricity. One way of dealing with this effect is to ascribe each atom with an effective charge, named the Born effective charge, $Z^{⋆}$ , which, more formally, is the first derivative of polarization with respect to atomic displacement. Using this effective charge in our freshman physics formula: $\vec{p} = Z^{⋆} Δ \vec{u}$ , gives a more accurate estimate of the polarization [4].

The electronic ferroelectricity in barium titanate points in the same direction as the ionic ferroelectricity, but this is not true in all materials. For example, in ${HoMn}_{2} O_{5}$ , where the polarization is driven by magnetic ordering, the electronic contribution to the polarization is in the opposite direction to the ionic contribution, but the two have nearly the same value, so the overall polarization is low for this material [5].

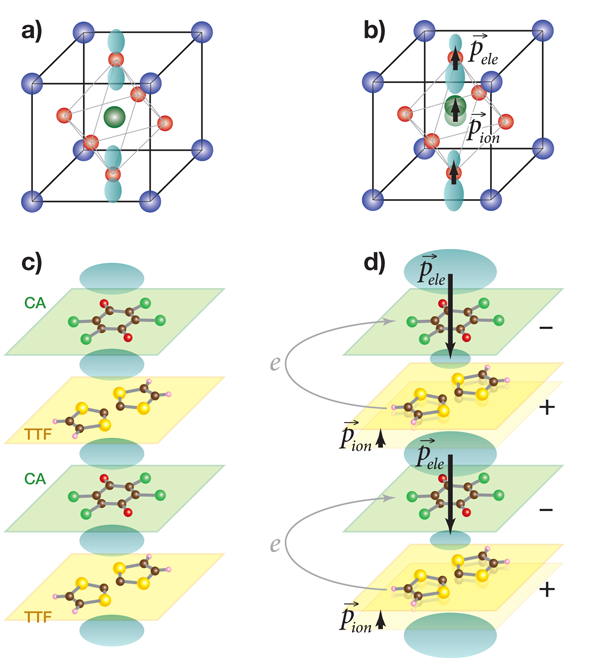
To find a case where the electronic contribution has a dominant effect, one must look to a different type of ferroelectric than the oxide compounds mentioned above. The organic molecular crystal tetrathiafulvalene-p-chloranil (TTF-CA) is a ferroelectric composed of alternating stacks of TTF [a double-ring molecule with formula ( $H_{2} C_{2} S_{2} C)_{2}$ ] and CA (a single-ring molecule with formula $C_{6} {Cl}_{4} O_{2}$ ). Above $81 K$ , each of the molecules in the stack is neutral, but below this temperature, the TTF donates an electron to CA in a neutral to ionic transition [6]. The ionized molecules shift relative to each other, creating alternating long and short bonds between the stacks (see bottom of Fig. 1).

As in other ferroelectric materials, there is also a shift of the electronic weight, but for TTF-CA it was predicted by first-principles density-functional theory that the electronic polarization could not only oppose the ionic polarization but also be greater in magnitude. As a consequence, the overall polarization direction should presumably be in the opposite direction to the ionic displacement [7], or to say it in another way, the sign of the Born effective charge, $Z^{⋆}$ , of the molecules in the crystal should be opposite to their ionic charge! This overpowering of the ionic polarization by the electronic polarization has been convincingly demonstrated for the first time by Kobayashi et al. [1]. They have performed synchrotron x-ray diffraction measurements of the crystal structure in TTF-CA and linked them to electrical measurements of the polarization. The comparison shows that the polarization direction is indeed in the opposite direction to what the ionic displacements would predict. Furthermore, the polarization they measure is quite large, and hence potentially useful, for example, as a way of storing information in a nonvolatile memory device.

The results of Kobayashi et al. give us much to think about. The switching that is demonstrated here is from one polarized state to another equivalent state, i.e., when the electronic polarization switches, the ionic polarization also switches to oppose the applied electric field. However, if a sufficiently high electric field were applied, it may be possible that the ionic polarization would switch its direction to align with the field and the electronic polarization as well. We might then see the triple hysteresis loop that is the hallmark of ferrielectricity, in which dipoles on different sites within a crystal have different magnitudes and antiferroelectric ordering (most commonly seen in liquid crystals [8]). Finally, it would be fascinating to combine TTF-CA with more conventional ferroelectrics in a multilayer to see what happens when ionic ferroelectricity and electronic ferroelectricity meet at an interface.

References

K. Kobayashi, S. Horiuchi, R. Kumai, F. Kagawa, Y. Murakami, and Y. Tokura, Electronic Ferroelectricity in a Molecular Crystal with Large Polarization Directing Antiparallel to Ionic Displacement, Phys. Rev. Lett. 108, 237601 (2012)
R. D. King-Smith and D. Vanderbilt, “Theory of Polarization of Crystalline Solids,” Phys. Rev. B 47, 1651 (1993)
Ph. Ghosez, J.-P. Michenaud, and X. Gonze, “Dynamical Atomic Charges: The Case of ABO3 Compounds,” Phys. Rev. B, 58, 6224 (1998)
A much more detailed discussion of ferroelectricty in perovskite oxide ferroelectrics can be found in Physics of Ferroelectrics: A Modern Perspective, edited by C. H. Ahn, K. M. Rabe, and J.-M. Triscone (Springer, New York, 2007)[Amazon][WorldCat]; or M. Dawber, K. M. Rabe, and J. F. Scott, “Physics of thin-film ferroelectric oxides,” Rev. Mod. Phys. 77, 1083 (2005)
G. Giovannetti and J. van den Brink, “Electronic Correlations Decimate the Ferroelectric Polarization of Multiferroic HoMn{2}O{5},” Phys. Rev. Lett. 100, 227603 (2008)
J. B. Torrance, J. E. Vazquez, J. J. Mayerle, and V. Y. Lee, “Discovery of a Neutral-to-Ionic Phase Transition in Organic Materials,” Phys. Rev. Lett. 46, 253 (1981)
G. Giovannetti, S. Kumar, A. Stroppa, J. van den Brink, and S. Picozzi, “Multiferroicity in TTF-CA Organic Molecular Crystals Predicted through Ab Initio Calculations,”Phys. Rev. Lett. 103, 266401 (2009)
A. Fukuda, Y. Takanishi, T. Isozaki, K. Ishikawa, and H. Takezoe, “Antiferroelectric chiral smectic liquid crystals,” J. Mater. Chem. 4, 997 (1994)

About the Author

Matt Dawber is an Assistant Professor in the Department of Physics and Astronomy at Stony Brook University. He has held this position since 2008, after completing his Ph.D. at the University of Cambridge, UK, in 2003, and postdoctoral work at the University of Geneva, Switzerland. All of which is very far from his original home town of Sydney, Australia. Matt’s research involves ferroelectric materials, mostly as thin films, with a current focus on artificially layered ferroelectric superlattices.