Matter Waves and Quantum Correlations

Mihai A. Macovei

Viewpoint

Matter Waves and Quantum Correlations

Max-Planck-Institut für Kernphysik, Saupfercheckweg 1, D-69117 Heidelberg, Germany

June 25, 2012• Physics 5, 70

Colliding matter waves from a Bose-Einstein condensate violate a relation called the Cauchy-Schwarz inequality, proving that such interactions must be considered quantum mechanically.

Figure caption — **Figure 1:** (Top panel) Spherical halo of scattered atoms created by four-wave mixing processes. (Bottom panel) The CSI coefficient $C$ as a function of the number of zones $M = V_{data} / V$ . The atomic sphere was cut into $8$ polar and $2$ – $80$ azimuthal zones. The arrangement of zones for $M = 16$ and $M = 32$ is depicted in the upper bottom panel [3].

Quantum effects in light-matter interaction have always intrigued scientists. Such effects may result in quantum particle-particle correlations, for instance. The first measurement of an intensity-intensity correlation function was performed by Hanbury-Brown and Twiss [1], while the theoretical basis for the full quantum characterization of light was introduced by Glauber [2]. Therefore, researchers now have efficient tools in their hands to probe light fields for quantum signatures. Remarkably, these correlations have now been measured for matter waves too, as described in Physical Review Letters by Karen Kheruntsyan at the University of Queensland, Australia, and colleagues [3]. In this paper, they report violation of an important relation for atom number correlations, called the Cauchy-Schwarz inequality, which indicates clear quantum effects in the interaction of matter waves. The correlated atoms have large spatial separations and therefore this work opens new opportunities for extending fundamental quantum-nonlocality tests to ensembles of massive particles.

To understand the character of these correlations, consider a “two-mode problem,” described by boson creation and annihilation operators $a_{i}^{†}$ and $a_{j}$ ( $i, j = 1, 2$ ), where the modes could be populated photons of different frequencies or momenta, for example. The creation operator would correspond to the emission of a particle and the annihilation operator accounts for particle absorption. In this case, the normalized second-order correlation functions are defined as follows [4]: $g_{i j}^{(2)} (τ) = G_{i j}^{(2)} (τ) / (n_{i} n_{j}) \equiv 〈 a_{i}^{†} a_{j}^{†} (τ) a_{j} (τ) a_{i} 〉 / (〈 a_{i}^{†} a_{i} 〉 〈 a_{j}^{†} a_{j} 〉)$ . The quantity $g_{i j}^{(2)} (τ)$ can be interpreted as a measure of the probability of detecting one particle emitted in mode $i$ and another particle emitted in mode $j$ , with time delay $τ$ . $g_{i j}^{(2)} < 1$ characterizes sub-Poissonian, $g_{i j}^{(2)} > 1$ super-Poissonian, and $g_{i j}^{(2)} = 1$ Poissonian statistics. $g_{i j}^{(2)} (τ) > g_{i j}^{(2)} (0)$ is the condition for antibunching, whereas $g_{i j}^{(2)} (τ) < g_{i j}^{(2)} (0)$ means particle bunching. Sub-Poissonian statistics, together with antibunching, are characteristics of nonclassical effects. Superbunching is the situation where $g_{i j}^{(2)} (0) > 2$ . More specifically, correlation functions with $i = j$ describe the particle statistics of the field emitted in one mode, and $g_{i \neq j}^{(2)} (0)$ the cross-correlations between the field emission in two different modes, respectively. Anticorrelation (correlation) occurs when $g_{i j}^{(2)} (0)$ is less (larger) than unity.

In tests of whether a system exhibits quantum correlations, the Bell inequalities are widely known. A less familiar and less stringent test between quantum theory and classical electromagnetic theory is called the Cauchy-Schwarz inequality (CSI). However, assessing the CSI is a precursor to more restrictive tests of nonclassical behavior and quantumness. It is defined as follows: $[g_{i \neq j}^{(2)}]^{2} \leq g_{i i}^{(2)} g_{j j}^{(2)}$ . Stronger-than-classical correlation violating this inequality would require $[g_{i \neq j}^{(2)}]^{2} > g_{i i}^{(2)} g_{j j}^{(2)}$ , i.e., the cross-correlations between particles emitted in two different modes are larger than the correlation between particles emitted in the individual modes. As a consequence, the violation of the CSI is a nonclassical characteristic of light fields. We further define the degree of violation of CSI by introducing the correlation coefficient, $C = G_{i j}^{(2)} / \sqrt{G_{i i}^{(2)} G_{j j}^{(2)}}$ , that is smaller than unity for classical processes, but can be larger than unity for states with stronger-than-classical correlations.

The first observation of a violation of this inequality, i.e., CSI, was obtained by Clauser by using an atomic two-photon cascade system [5]. Large violations created by four-wave mixing have been obtained in the photon-counting [6] and macroscopic regimes [7], respectively. It was predicted that photon scattering by a collection of few-level atoms in incoherent environments also leads to violation of CSI [8].

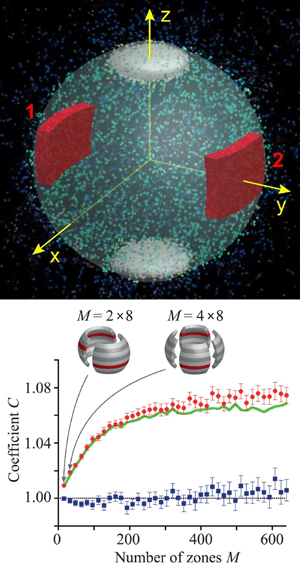
Now, these correlations have been exported to matter waves. Kheruntsyan et al. [3] have demonstrated a violation of CSI via four-wave mixing in matter-wave optics using pair-correlated atoms formed in a collision of two Bose-Einstein condensates (BEC) of metastable helium. A cigar-shaped BEC containing about $10^{5}$ metastable helium atoms was split by Bragg diffraction into two parts traveling at $\pm 2 v_{rec}$ , where $v_{rec} = 9.2 cm/s$ is the recoil velocity. Some of the atoms remain at rest with zero velocity. The binary collision take place between all atoms producing scattering halos populated by pairs of atoms of opposing velocities (see Fig. 1). The detected nearly spherical halo has a radius in velocity space of about the recoil velocity. The halo diameter in position space at the detector was about $6 cm$ . To focus only on those atoms that were spontaneously scattered, the strength of correlations was quantified in a spherical shell of radial thickness $0.9 < v / v_{rec} < 1.1$ that defines the total volume of the analyzed region, $V_{data}$ .

An important issue here is that the above two-mode particle-particle correlations have to be generalized to a multimode situation. This generalization includes the fact that in matter-wave optics, the correlations are a function of the particle’s momentum. Therefore, one must define an appropriate integration domain over multiple momentum modes. As a consequence, it was found that the peak cross-correlation for pairs of atoms scattered in opposite directions is smaller than the peak autocorrelation for pairs of atoms propagating in the same direction. Thus the CSI is not violated if one uses the peak heights of correlation functions, i.e., the two-mode approximation.

In order to detect violation of the CSI, the authors [3] came up with the nice idea to use integrated correlation functions that correspond to an atom number $n$ in a particular volume $V$ . When the two volumes correspond to diametrically opposed correlated pairs of zones (red boxes in Fig. 1, top panel), the parameter $C$ is greater than unity, violating the CSI (red and green curves in Fig. 1, bottom panel). In contrast, for the two identical neighboring volumes containing uncorrelated atom pairs, the CSI is not violated (blue line in Fig. 1, bottom panel). Furthermore, large integration volumes (that is, when the halo is cut into a small number of zones for analysis) results in weak violation, while using smaller volumes (many zones) increases the violation. This behavior is due to the fact that larger volumes tend to behave classically. An intuitive picture of this effect is that the opposite scattered atom pairs get correlated via four-wave mixing processes. The observed nonclassical effects prove that scattering atoms should be treated quantum mechanically and cannot be described by classical stochastic random variables theory.

Finally, a potential interesting property of these results is that the atom pairs have large spatial separations (several cm) and are well suited for further investigations of Einstein-Podolsky-Rosen entanglement and Bell’s inequalities using atoms. Thus matter wave optics has reached the point where quantum correlated atomic states can be successfully created and their fascinating features can be explored.

References

R. Hanbury Brown and R. Q. Twiss, ”Correlation between Photons in two Coherent Beams of Light,” Nature 177, 27 (1956)
R. J. Glauber, ”The Quantum Theory of Optical Coherence,” Phys. Rev. 130, 2529 (1963); ”Coherent and Incoherent States of the Radiation Field,” 131, 2766 (1963)
K. V. Kheruntsyan, J-C. Jaskula, P. Deuar, M. Bonneau, G. B. Partridge, J. Ruaudel, R. Lopes, D. Boiron, and C. I. Westbrook, ”Violation of the Cauchy-Schwarz Inequality with Matter Waves,” Phys. Rev. Lett. 108, 260401 (2012)
D. F. Walls, and G. J. Milburn, Quantum Optics (Springer-Verlag, New York, 1995)[Amazon][WorldCat]
J. F. Clauser, ”Experimental distinction between the quantum and classical field-theoretic predictions for the photoelectric effect,” Phys. Rev. D 9, 853 (1974)
P. Kolchin, S. Du, C. Belthangady, G. Y. Yin, and S. E. Harris, ”Generation of Narrow-Bandwidth Paired Photons: Use of a Single Driving Laser,” Phys. Rev. Lett. 97, 113602 (2006)
A. M. Marino, V. Boyer, and P. D. Lett, ”Violation of the Cauchy-Schwarz Inequality in the Macroscopic Regime,” Phys. Rev. Lett. 100, 233601 (2008)
M. Macovei, J. Evers, and C. H. Keitel, ”Quantum correlations of an atomic ensemble via an incoherent bath,” Phys. Rev. A 72, 063809 (2005)

About the Author

Since 2004, Mihai Macovei has been a researcher at the Max Planck Institute for Nuclear Physics, Heidelberg, Germany. He received his Ph.D. at the Institute of Applied Physics, Academy of Sciences of Moldova, and was a fellow of the Alexander von Humboldt Foundation while at Freiburg University, Germany. His research interests include collective phenomena in quantum optics, quantum interference and decoherence, and quantum correlations.