High Currents, When Hot

Jan van Ruitenbeek

Viewpoint

High Currents, When Hot

Kamerlingh Onnes Laboratory, Leiden University, The Netherlands

July 30, 2012• Physics 5, 85

Experiments on electron transport across single molecules show evidence of enhancement of the current at higher temperatures due to suppression of destructive quantum interference.

Figure caption — **Figure 1:** One of the molecules studied by Ballmann *et al.* is schematically represented above, as coupled between gold metal leads. The nearest molecular orbital is quasidegenerate, such that electrons can chose between two orbitals to cross the molecule. The two paths in orbital space interfere destructively, and this interference is destroyed by interactions in one of the arms with molecular vibrations.

The initial concepts of molecular electronics were formulated many decades ago, but it was not until the 1990s that the tools became available for experiments. The prospects of utilizing the design and synthesis capabilities of organic chemistry for employing molecules as the active elements in electronic circuits are tantalizing. This past decade, experimental research has been mostly concerned with the very challenging problem of bridging the size gap between the smallest structures feasible by nanofabrication for the leads, and the size of the molecules to be studied. Self-assembly is a key element in this endeavor, but since we cannot control nor image this process in detail, much depends on a proper characterization of the devices produced. The present state of affairs has been nicely summarized in the book by Cuevas and Scheer [1], and we may conclude that we have advanced to the point that single-molecule junctions can now be fabricated reliably.

The starting theoretical model in molecular transport goes back to the models developed for quantum dots that have been studied in detail before in mesoscopic physics, such as those defined by gates in two-dimensional electron gas systems. This model considers a number of discrete electronic states, which may include the electron-electron interactions within the dot, and a coupling of the dot to two metallic leads by a characteristic coupling energy. The quantum dot states are occupied up to the level just below the Fermi energy of the leads, and they are broadened by the coupling. Many of the results obtained to date have been interpreted in terms of this picture.

Writing in Physical Review Letters, Stefan Ballmann at the University of Erlangen-Nürnberg, Germany, and colleagues [2] present clear experimental evidence of the limited applicability of this simplified picture. They show that interesting new physics comes from those properties that distinguish molecules from typical quantum dots: First, molecules have a high degree of regular structure and symmetry. This implies that the levels are not randomly positioned, but their distribution reflects the real-space symmetry of the molecule. Of central importance to the results discussed by Ballmann et al. is the fact that such symmetry gives rise to (near) degeneracy of energy levels as a rule, not an exception. The second distinguishing characteristic of a molecular conductor is its floppyness: many vibration modes are active and they are strongly coupled to the electronic degrees of freedom.

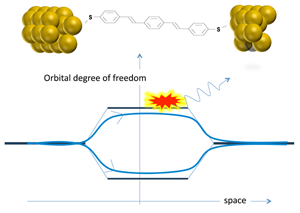
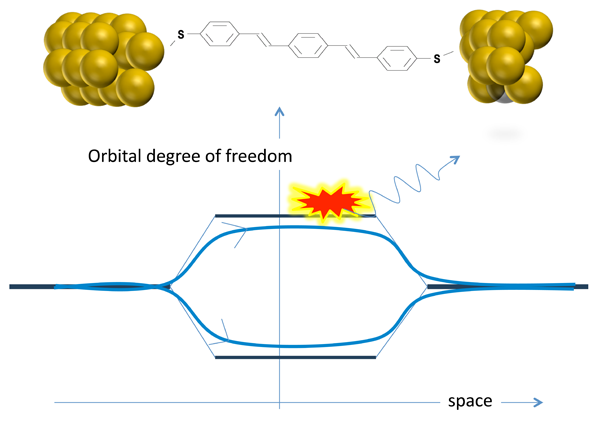
The third ingredient in the authors’ discussion of the results [2] is the interference of electron paths. This concept is at the heart of quantum mechanics and we have all been introduced to its principles through such famous examples as Young’s double slit experiment and the Aharonov-Bohm effect. However, the type of interference considered here is slightly more subtle: The electrons follow essentially the same trajectory in space, but they can choose between different types of molecular orbitals (Fig. 1). The orbitals differ in their symmetry, but the broadening of the levels gives rise to an overlap in the relevant energy window close to the Fermi energy, so that the electrons essentially see degenerate levels [3]. Guédon et al. [4] have recently presented experimental evidence for quantum interference effects in electron transport through a molecular bridge containing degenerate orbitals.

Quantum interference of electron trajectories can be suppressed when information about the choice of path is communicated in some form to the world outside. A very instructive demonstration of this principle in mesoscopic physics can be seen in the experiments by Buks et al. [5], where one of the arms of an Aharonov-Bohm ring was coupled to a point-contact detector through a tunable coupling, which allows the interference to be gradually quenched. In a recent theoretical analysis, Härtle et al. [6] have proposed that quantum interference of electron channels in molecules becomes suppressed when the electrons are coupled to the vibration modes of the molecule. This effect has now been demonstrated by Ballmann et al., albeit in a slightly indirect manner.

Their experiment involved the measurement of three different types of molecules in a so-called break junction configuration. For each of the molecules, the authors presented density-functional theory (DFT) calculations to show that the nearest molecular levels are quasidegenerate, which produces the destructive interference in the regions of overlap. At the lowest temperatures ( $< 10 K$ ), Ballmann et al. measured the differential conductance, $d I / d V$ , as a function of the potential difference applied between the two electrodes. At low bias they observed a very low current, but as the voltage bias window was opened wider, a pronounced step to higher conductance was observed, which then was seen to level off at still higher bias. This is the behavior expected from the naive starting model. However, as they raised the temperature to about $40 K$ , the current at bias values above the step was seen to increase significantly. Simple phonon-assisted tunneling effects would not produce such a large response. Artifacts, such as thermal expansion of the device, were eliminated by blind tests; in fact, the remarkable stability of the break junction devices allows for this experiment to be performed. The interpretation in terms of thermal breaking of interference was then put to the test by selecting a fourth molecular species having a different anchoring group, which DFT calculations predict to have just regular, nondegenerate levels near the Fermi energy. Indeed, the temperature dependence in this case was found to be absent.

In further tests of the interpretation, the authors made an interesting additional observation: stretching of the molecular junction gives rise to an increase of conductance. Normally, one would expect the stretching of the junction to weaken the contacts and reduce the conductance, but such enhancements have been observed previously and have been attributed to the effects of changes in bond angles entirely within the framework of the starting model. However, by considering interference of orbitals, a more interesting interpretation of “interference tuning” was proposed: stretching reduces the overlap of the orbitals and thereby reduces destructive interference.

The way the coupling to phonons breaks the interference is slightly subtle. The “which-path effect” in the theory by Härtle et al. is hidden in the assumption of an asymmetry in the electron-phonon coupling between the two orbitals involved. For the effects to be observable, such asymmetry must be present in the system. In view of the many vibration modes available for each molecule, one should not be surprised that some of them couple more strongly to one of the two orbitals than to the other.

As an experimentalist working with molecular wires, one of the questions that puzzles me most is the following: Ballman et al. recorded changes of conductance with temperature at fairly high bias voltages, of the order of $1 V$ . At such high bias, the effective lattice temperature for the ion cores in the molecule is expected to be raised to very high values, which could be much above $1000 K$ according to some estimates. If so, why would a relatively small increase in temperature of only $30 K$ produce such a large effect? Clearly, there are still many questions to be answered and these results will stimulate further experiments in several laboratories, including our own, to probe interference effects and the role of the electron-phonon coupling.

References

J. C. Cuevas and E. Scheer, Molecular Electronics: An Introduction to Theory and Experiment (World Scientific, Singapore, 2010)[Amazon][WorldCat]
S. Ballmann, R. Härtle, P. B. Coto, M. Elbing, M. Mayor, M. R. Bryce, M. Thoss, and H. B. Weber, ”Experimental Evidence for Quantum Interference and Vibrationally Induced Decoherence in Single-Molecule Junctions,” Phys. Rev. Lett. 109, 056801 (2012)
G. C. Solomon et al., “Molecular Origins of Conduction Channels Observed in Shot-Noise Measurements,” Nano Lett. 6, 2431 (2006)
C. M. Guédon et al., “Observation of Quantum Interference in Molecular Charge Transport,” Nature Nanotech. 7, 305 (2012)
E. Buks, R. Schuster, M. Heiblum, D. Mahalu, and V. Umansky, “Dephasing in Electron Interference by a ‘Which-Path’ Detector,” Nature 391, 871 (1998)
R. Härtle, M. Butzin, O. Rubio-Pons, and M. Thoss, Quantum Interference and Decoherence in Single-Molecule Junctions: How Vibrations Induce Electrical Current,” Phys. Rev. Lett. 107, 046802 (2011)

About the Author

Jan van Ruitenbeek received his Ph.D. in physics from the Radboud University of Nijmegen, Netherlands, in 1985. He performed his postdoctoral research work with the Max-Planck Institute at the High Field Magnet Laboratory in Grenoble, France. Since 1988 he has held an appointment with the Leiden Institute of Physics at Leiden University, The Netherlands, and in 2003 he became full professor. In 1994 he spent his sabbatical with the Quantronics group at the CEA in Saclay, France. He pioneered the break junction technique for atomic and molecular wires. His current research interests are in the field of low-temperature experimental physics with a focus on electron transport in nanostructures.