Transition Path Times for DNA and RNA Folding from Force Spectroscopy

Gerhard Hummer; William A. Eaton

Viewpoint

Transition Path Times for DNA and RNA Folding from Force Spectroscopy

Laboratory of Chemical Physics, National Institute of Diabetes and Digestive and Kidney Diseases, National Institutes of Health, Bethesda, MD 20892-0520, USA

August 6, 2012• Physics 5, 87

Experiments show that the times required to cross the barrier for the folding and unfolding of different nucleic acids are consistently about a few microseconds, despite many orders of magnitude differences in rate coefficients.

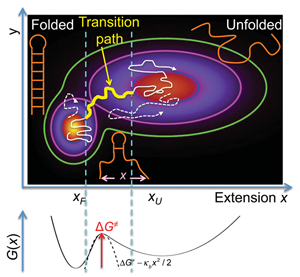
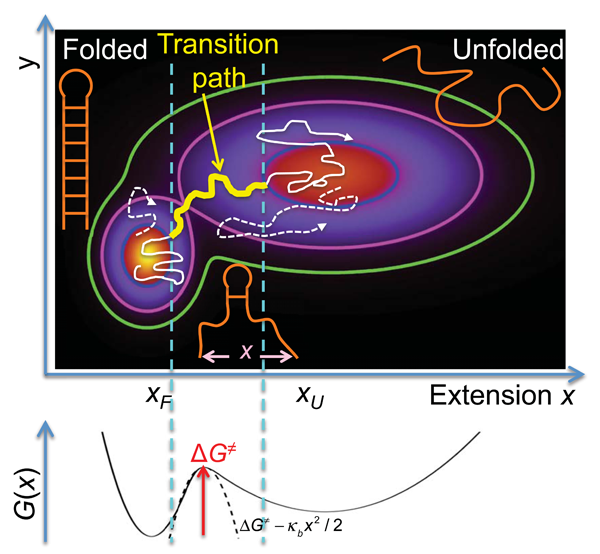
Figure caption — **Figure 1:** Transition path projected on schematic two-dimensional free-energy surface. The surface is indicated by contour lines and coloring, with the red and yellow areas bounded by blue contours corresponding to low (favorable) free energies. The molecular extension $x$ in the horizontal direction and a coordinate $y$ , not observed directly in experiment, together separate the folded (left) and unfolded basins (right), shown with representative structures (orange) of a DNA hairpin (folded: left; folding transition state: middle; coil: right). The molecule spends the vast majority of time in one or the other basin, with very rare but very rapid transitions between them. The transition path is the (yellow thick) segment of the unfolding trajectory (continuous white), directly connecting the folded ( $x < x_{F}$ ) and unfolded states ( $x > x_{U}$ ), whose boundaries are indicated by dashed vertical lines. Thin white dashed lines indicate trajectories failing to cross the barrier. The bottom panel shows the corresponding one-dimensional free-energy surface, obtained by integrating out also $y$ , to define the relevant quantities entering the approximate expression Eq. ( $2$ ) used by Neupane *et al.*[1] for the mean transition path time [4, 8].

The folding of proteins and nucleic acids from disordered to highly ordered structures serves as a prime example of complex conformational dynamics in the condensed phase. Beyond establishing the connection between the one-dimensional information contained in the sequences of these biopolymers and their three-dimensional structures in the folded state, a central problem in biological physics is the development of a rigorous and quantitative understanding of folding mechanisms. All the mechanistic information on how a biopolymer folds is contained in its transition paths, the tiny segments of an equilibrium trajectory during which the molecule actually crosses the barrier between folded and unfolded states, after a very large number of failed attempts (see Fig. 1).

Folding transition paths are a single-molecule property and have not been observed by experiment for either proteins or nucleic acids, but this situation is rapidly changing [1,2]. Using single-molecule fluorescence experiments, Chung et al. [2] measured average transition path times that are within a factor of $5$ for proteins whose folding rates differ by $4$ orders of magnitude. Given the complexity of the structural rearrangements involved in folding, this finding is surprising but, interestingly, can be readily explained by the theory for diffusion of a single particle on a one-dimensional free-energy surface [3,4]. Now, in a paper in Physical Review Letters, Krishna Neupane at the University of Alberta, Canada, and colleagues [1] exploit this theory to greatly extend the work of Chung et al. [2]. In technologically demanding optical-tweezer experiments analyzed using energy landscape theory, they find remarkably similar low-microsecond transition times for a wide range of nucleic acids, whose theoretically extrapolated unfolding rates in the absence of force range over $18$ orders of magnitude [1]. These single-molecule fluorescence and force spectroscopic experiments represent a major step forward toward the goal of observing transition paths in experiments, i.e., of watching proteins and nucleic acids fold one molecule at a time.

Chung et al. [2] determined the transition path time from a photon-by-photon analysis [5] of hundreds of transition events observed in fluorescence resonant energy transfer experiments. In the new work, Neupane et al. [1] studied folding transition paths by mechanical pulling on the ends of nucleic acids tethered by DNA handles to optically trapped beads. With this setup, a constant piconewton (pN) force was exerted on the nucleic acid, and the folding and unfolding events were detected by monitoring the bead distance, which reported on the nanometer (nm) changes in the molecular extension. Impressive statistics only partly explain their success, since the time resolution of the experiments is inherently limited. For a laser trap with a spring constant $k \sim 0.1$ pN/nm and a bead of radius $R \sim 1$ micrometers, the diffusional relaxation time, assuming Stokes-Einstein friction, is on the order of $100$ microseconds, setting a limit on what can be resolved directly without using smaller beads and/or stiffer traps. To overcome this limit, Neupane et al. [1] employed formalisms of energy landscape theory.

Theory [3], simulation [6], and ensemble experiments [7] for proteins with two-state behavior support the postulate of the energy landscape formalism that (un)folding transitions can be described by diffusive dynamics on a low-dimensional, free-energy surface with a single barrier separating the folded and unfolded states. For the two-dimensional free-energy surface in Fig. 1, $x$ is the molecular extension probed by the pulling experiments [1], and $y$ is an unresolved coordinate that helps separate the two states, folded and unfolded. Along the transition path, which may include transient visits to low-population intermediates, the mechanistically relevant changes occur; so the transition path is by far the most important trajectory segment.

For dynamics described by the Smoluchowski diffusion equation, an analytic expression relates the duration of the transition path between two states on a one-dimensional free-energy surface to the barrier height $Δ G^{\neq}$ and diffusivity $D$ [4]. An accurate approximation derived by Szabo [8] shows that the average transition path time $\bar{τ_{T P}}$ grows only logarithmically with $Δ G^{\neq}$ for a high and parabolic free-energy barrier, in contrast to the exponentially growing average time that a molecule resides or “waits” in a state before a “lucky” series of thermal kicks results in passage over the barrier. The rate coefficient, the reciprocal of this average time, provides the conventional measure of speed of a process in kinetic experiments.

To employ this formalism, Neupane et al. [1] monitored fluctuations in the extension $x$ of the molecules in presence of a constant external force. The molecular extensions are a reasonable choice of reaction coordinate for the folding by zipping and unfolding by unzipping of nucleic acid hairpins and similar structures (see Fig. 1). The corresponding one-dimensional free-energy surface, $G (x)$ vs $x$ (schematically shown in Fig. 1, bottom) was estimated from the observed distributions, corrected for the effects of the trap and DNA handle and instrument response by deconvolution. Knowing $G (x)$ , the diffusivity $D$ could be estimated from the measured rate coefficients for (un)folding (the reciprocal of the mean residence time), and then from $G (x)$ and $D$ , the mean transition path time $\bar{τ_{T P}}$ could be calculated (see also Fig. 1).

Neupane et al. [1] validated their estimates of $Δ G^{\neq}$ and $D$ by measuring unfolding times under a continuously increasing force, interpreted with a different, but related theory [9]. By fitting theoretical expressions to the measured data, Neupane et al. obtained independent estimates of the unfolding barrier height $Δ G^{\neq}$ and the diffusivity $D$ that led to consistent transition path times for the DNA hairpins. For the more complex RNA structures, only this latter technique was used to estimate $\bar{τ_{T P}}$ . Neupane et al. further backed up their calculated low-microsecond transition path times by estimating an upper bound of $\sim 50$ microseconds directly from the observed bead trajectories, consistent with the rough estimate of the bead relaxation time above. Moreover, the observed diffusion coefficients $D$ are consistent with earlier estimates for DNA hairpin zipping and unzipping.

Measuring average transition path times is only a first step. Future studies will aim to characterize the evolution of structure during transition paths. At present, researchers can only address this by molecular simulations [10,11]. However, we are optimistic that observation of individual transition paths will soon become possible in experiment, through continued improvements in time resolution and the application of methods to probe several intramolecular distances simultaneously.

References

K. Neupane, D. B. Ritchie, H. Yu, D. A. N. Foster, F. Wang, and M. T. Woodside, ”Transition Path Times for Nucleic Acid Folding Determined from Energy-Landscape Analysis of Single-Molecule Trajectories,” Phys. Rev. Lett. 109, 068102 (2012)
H. S. Chung, K. McHale, J. M. Louis, and W. A. Eaton, “Single-Molecule Fluorescence Experiments Determine Protein Folding Transition Path Times,” Science 335, 981 (2012)
J. D. Bryngelson and P. G. Wolynes, “Intermediates and Barrier Crossing in a Random Energy Model (with Applications to Protein Folding),” J. Phys. Chem. 93, 6902 (1989)
G. Hummer, “From Transition Paths to Transition States and Rate Coefficients,” J. Chem. Phys. 120, 516 (2004)
I. V. Gopich and A. Szabo, “Decoding the Pattern of Photon Colors in Single-Molecule FRET,” J. Phys. Chem. B 113, 10965 (2009)
R. B. Best and G. Hummer, “Coordinate-Dependent Diffusion in Protein Folding,” Proc. Natl. Acad. Sci. USA 107, 1088 (2010)
J. Kubelka, E. R. Henry, T. Cellmer, J. Hofrichter, and W. A. Eaton, “Chemical, Physical, and Theoretical Kinetics of an Ultrafast Folding Protein,” Proc. Natl. Acad. Sci. USA 105, 18655 (2008)
H. S. Chung, J. M. Louis, and W. A. Eaton, “Experimental Determination of Upper Bound for Transition Path Times in Protein Folding from Single-Molecule Photon-by-Photon Trajectories,” Proc. Natl. Acad. Sci. USA 106, 11837 (2009)
O. K. Dudko, G. Hummer, and A. Szabo, “Theory, Analysis, and Interpretation of Single-Molecule Force Spectroscopy Experiments,” Proc. Natl. Acad. Sci. USA 105, 15755 (2008)
P. G. Bolhuis, D. Chandler, C. Dellago, and P. L. Geissler, “Transition Path Sampling: Throwing Ropes over Rough Mountain Passes, in the Dark,” Annu. Rev. Phys. Chem. 53, 291 (2002)
K. Lindorff-Larsen, S. Piana, R. O. Dror, and D. E. Shaw, “How Fast-Folding Proteins Fold,” Science 334, 517 (2011)

About the Authors

Gerhard Hummer received his Ph.D. in physics for work done jointly at the University of Vienna and at the Max Planck Institute for Biophysical Chemistry. He is a Senior Investigator in the Laboratory of Chemical Physics at the National Institutes of Health, and a recipient of the 2010 Raymond and Beverly Sackler International Prize in Biophysics. His research in biological physics focuses on the theory and simulation of biomolecular systems, including the theory of force spectroscopy.

William Eaton received his M.D. and Ph.D. in molecular biology from the University of Pennsylvania. He is an NIH Distinguished Investigator in the Laboratory of Chemical Physics at the National Institutes of Health, and recipient of the 2012 Max Delbrück Prize in Biological Physics of the American Physical Society. His research in biological physics focuses on single molecule fluorescence and statistical mechanical models for protein folding.