Getting into a Proper Jam

Eric Corwin

Viewpoint

Getting into a Proper Jam

Eric Corwin

Department of Physics, University of Oregon, Eugene, OR 97403, USA

August 27, 2012• Physics 5, 97

Numerical simulations are revealing general properties of jammed states of matter.

Figure caption — **Figure 1:** Pictorial energy ( $U$ ) landscape for a finite-size set of soft spheres for which thermal fluctuations can be neglected. $| r 〉$ denotes the degree of freedom of particle positions, and $Δ L$ the deformation of the shape of the simulation box. Dagois-Bohy *et al.* show that jammed states identified by compression-only (CO) methods minimize the energy with respect to the particles’ positions only and may be unstable to shear. Shear-stabilized packings (SS) minimize the energy with respect to both particle positions and the box shape and are thus properly jammed. Goodrich *et al.* analyze how the properties of shear- and compression-stable states scale with size, finding the evidence that jamming can be described as a true phase transition.

The study of jammed systems began as a culinary curiosity in 1727, when the Reverend Stephen Hales studied how peas pack when compressed in an iron pot [1]. Fill a pot with peas and you can run your hand through them, because they can flow out of the way much like a liquid would. But as pressure, and thus the density, is increased, you will find that there is a critical point, above which the peas “jam” into a stable amorphous solid. This behavior is very general. Pretty much everything composed of discrete chunks large enough that thermal fluctuations can be ignored can go through a jamming transition: colloids in solution, a pile of sand, a jar full of candies, even cars in a traffic jam.

Since the work of Hales, and at an accelerating pace since the late 1950s, jamming has emerged as a fascinating research topic and as a paradigm for studying the formation of amorphous solids, in particular, glasses [2]. Many experimental techniques have been applied to the study of jammed states. However, experimentally, it is extremely difficult to access the complex dynamics of systems very near the jamming transition. Instead, researchers increasingly rely on numerical simulations, which allow them to explore situations extraordinarily close to the jamming threshold. Unfortunately, simulations are limited to a finite (and small) number of particles. One kilogram of beach sand can easily contain $30$ billion individual grains, far beyond the capabilities of even the largest computing schemes. As a consequence of such experimental and computational hurdles, a general theory for the description of jammed systems is still lacking.

By simulating the jamming behavior of finite-size systems, two papers in Physical Review Letters come to general conclusions on the nature of jamming transitions that may help shape a unified theory of jamming. Simon Dagois-Bohy, at Leiden University in the Netherlands, and co-workers expose the pitfalls of interpreting simulations in finite-size systems, showing that properly jammed systems must be stable not only to compression but also to shear [3]. In an independent but related paper, Carl Goodrich, at the University of Pennsylvania, Philadelphia, and co-workers investigate the scaling behavior of finite-size systems jammed under varying constraints and provide strong evidence that the jamming transition can in fact be considered a phase transition [4].

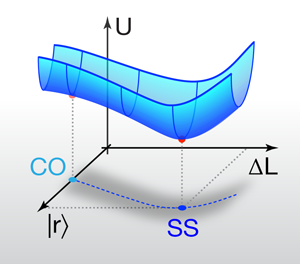
Dagois-Bohy et al. demonstrate that widely used simulation approaches for finite numbers of particles can produce arrangements of packed particles which appear to be jammed and yet will fall apart at the slightest shear. Such simulations assume two-dimensional geometries with periodic boundary conditions, in which particles at the top of the system press against those at the bottom, and particles on the left side press against those on the right (think of the surface of a torus). The results can be easily generalized to three dimensions. Typically, to simulate the density increase that leads to jamming, spheres are inflated until a nonzero pressure is achieved in the system, a protocol that Dagois-Bohy and colleagues label compression-only. Until now, it has been widely believed that this condition corresponds to a jammed state, i.e., one that is stable to both compression and shear. And, indeed, Dagois-Bohy et al. found that this approach yields packings that are stable to compression, as evidenced by the fact that these arrangements have positive bulk moduli: increased pressure results in decreased volume. However, when they subjected these seemingly jammed systems to shear stresses they found that an alarmingly large number of them were unstable and simply fell apart. Worse yet, the probability of finding improperly jammed systems approached unity for simulations carried out at vanishingly small pressures, close to the jamming threshold.

How can this be? After all, a finite global pressure means that there is an energy cost associated with moving any particle within the system, and thus the system should be stable to shear stresses. The insight of Dagois-Bohy et al. was to realize that shear is created not only by the movement of individual particles within the simulation volume but also by a deformation of the boundaries of the volume itself. This deformation is an additional degree of freedom—one whose energy has not been accounted for and minimized in the simulation, as illustrated in Fig. 1. As such, it should be no surprise that these packings can be unstable to shear. To remedy this problem Dagois-Bohy and colleagues introduce an elegant and simple algorithm that they term shear stabilized, which allows the boundaries of the simulation box to deform as part of the energy minimization, leading to slightly nonsquare unit cells. By this trick, they are able to pinpoint those jammed packings that are stable to both compression and shear.

In their work, Goodrich and colleagues have turned the limitations of numerical simulations of finite-sized systems to their benefit. By varying the size of their simulations, and requiring both shear and compression stability for proper jamming, they provide insights into the nature of the jamming transition that fixed-size simulations, even for an arbitrarily large size, cannot deliver. For a system of $N$ particles in $d$ dimensions, jamming means that every degree of freedom (with the exception of the $d$ degrees of freedom related to bulk translations) must be constrained. In a jammed system these constraints are provided by contacts between particles. A naive accounting would lead to $d \cdot N - d$ contacts. Goodrich and colleagues demonstrate that this isn’t enough. They demonstrate that in finite-sized systems one additional contact is needed for the system to have a positive bulk modulus (as in the compression-only packings above) and yet another $\frac{1}{2} d \cdot (d + 1) - 1$ contacts are needed to have a positive shear modulus (as in the shear-stabilized packings above).

They tested these predictions by simulating two- and three-dimensional systems ranging from the very small ( $N = 64$ ) to the relatively large ( $N = 4096$ ). Simulating systems under smaller and smaller pressures, and thus closer and closer to the jamming transition point, they found that the onset of stable jamming corresponds precisely to the number of contacts they predicted. As they increased the density above jamming, they showed that the bulk properties of their packings, such as the bulk and shear moduli, all scale with the excess number of contacts between particles. Remarkably, for all system sizes they are able to collapse these dependencies onto a master curve by scaling the data with exponents determined by their counting argument. Such finite-size scaling is the hallmark of a phase transition [5]. The idea that jamming is a collective phenomenon related to an underlying phase transition has emerged in recent work [2,6,7] and the paper by Goodrich et al. further supports this claim. Their results are consistent with jamming being either a random first-order or a mean-field second-order transition.

The papers of Dagois-Bohy et al. and Goodrich et al. deliver two key messages. Dagois-Bohy and colleagues show that properly jammed states must be stable to both compression and shear, raising a potentially troubling question: Will the existing body of computational work, overwhelmingly based on compression-only methods, stand the test of shear-stabilized simulations and, more importantly, of jamming experiments? Given the observations of Dagois-Bohy et al., it will be important to reexamine older theoretical results. Goodrich and colleagues support the important conclusion that jamming is in fact a phase transition. The fact that it has taken so long to reach such a sensible conclusion is indicative of the extreme difficulty in describing systems for which a well-defined statistical mechanics framework is not yet available. Researchers will now be called to answer a set of even harder questions: What will a mean-field theory that describes jamming look like? Will it be based on approaches that have proven useful for the study of the glass transition, such as mode coupling [8], and the replica method [9], or will it be something entirely different? Will a unifying theory emerge for the jamming and glass transition?

While the horizons of physics have stretched to encompass the extremes of the universe, it is remarkable that there are still fundamental puzzles awaiting us at the bottom of a bucket of sand.

References

S. Hales, Vegetable Staticks (W. and J. Innys and T. Woodward, London, 1727)[Amazon][WorldCat]
A. J. Liu and S. R. Nagel, “Jamming is Not Just Cool Any More,” Nature 396, 21 (1998)
S. Dagois-Bohy, B. P. Tighe, J. Simon, S. Henkes, and M. van Hecke, ”Soft-Sphere Packings at Finite Pressure but Unstable to Shear,” Phys. Rev. Lett. 109, 095703 (2012)
C. P. Goodrich, A. J. Liu, and S. R. Nagel, ”Finite-Size Scaling at the Jamming Transition,” Phys. Rev. Lett. 109, 095704 (2012)
R. J. Creswick, H. A. Farach, and C. P. Poole, Jr., Introduction to Renormalization Group Methods in Physics, (J. Wiley and Sons, London, 1992)[Amazon][WorldCat]
L. Berthier, G. Biroli, J.-P. Bouchaud, L. Cipelletti, D. El Masri, D. L’Hôte, F. Ladieu, and M. Pierno, ”Direct Experimental Evidence of a Growing Length Scale Accompanying the Glass Transition,” Science 310, 1797 (2005)
A. S. Keys, A. R. Abate, S. C. Glotzer, and D. J. Durian, ”Measurement of Growing Dynamical Length Scales and Prediction of the Jamming Transition in a Granular Material,” Nature Phys. 3, 260 (2007)
W. Götze, Complex dynamics of glass-forming liquids: A mode-coupling theory, International Series of Monographs on Physics Vol. 143 (Oxford University Press, Oxford, 2009)[Amazon][WorldCat]
G. Parisi and F. Zamponi, “Mean-Field Theory of Hard Sphere Glasses and Jamming,” Rev. Mod. Phys. 82, 789 (2010)

About the Author

Eric Corwin is an assistant professor of physics at the University of Oregon. He received his Ph.D. in physics from the University of Chicago and has worked in the Center For Soft Matter Research at New York University. His current research focuses on jamming and geometric frustration, in soft-condensed matter and in biophysics. For more information about his research visit phasmid.uoregon.edu.