Metal-Coated Waveguide Stretches Wavelengths to Infinity

Wenshan Cai

Viewpoint

Metal-Coated Waveguide Stretches Wavelengths to Infinity

School of Electrical and Computer Engineering, and School of Materials Science and Engineering, Georgia Institute of Technology, Atlanta, GA 30332, USA

January 2, 2013• Physics 6, 1

A zero refractive index at optical frequencies, as demonstrated in a new nanoscale waveguide, enables opportunities for better control and enhancement of light propagation in waveguides, as well as development of photonic nanocircuits.

Figure caption — **Figure 1:** (Top) Light-bending behaviors in materials with positive, near-zero, and negative indices of refraction. In the index-near-zero medium, the electromagnetic fields become homogeneous with a uniform phase distribution. (Bottom) The dispersion relations of a dielectric strip waveguide with an air cladding (green) and a plasmonic waveguide with a dielectric core surrounded by a metallic cladding (red). The black circles indicate the cutoff conditions. The two straight lines correspond to the light lines of vacuum ( $ω / k = c$ ) and glass ( $ω / k = c / n$ ), respectively, and the dashed line represents the dispersion curve of surface plasmons. The inset shows the electric field (arrows) and magnetic field (color map) of the zero-index mode at the cutoff frequency.

The index of refraction is arguably the most important parameter for an optical medium and is critically pertinent to most, if not all, of the phenomena of light in optical materials and devices. Recent advances in metamaterials, which are artificially structured media with engineered electromagnetic properties, have provided us with an unprecedented ability to realize unconventional values of the refractive index that were not considered possible in the past. Now, writing in Physical Review Letters [1], Ernst Vesseur of the FOM Institute for Atomic and Molecular Physics (AMOLF), Netherlands, and his colleagues have demonstrated a metallic waveguide that exhibits a zero refractive index at visible frequencies. Light in such a material has a spatially uniform phase, characterized by a quasi-infinite wavelength.

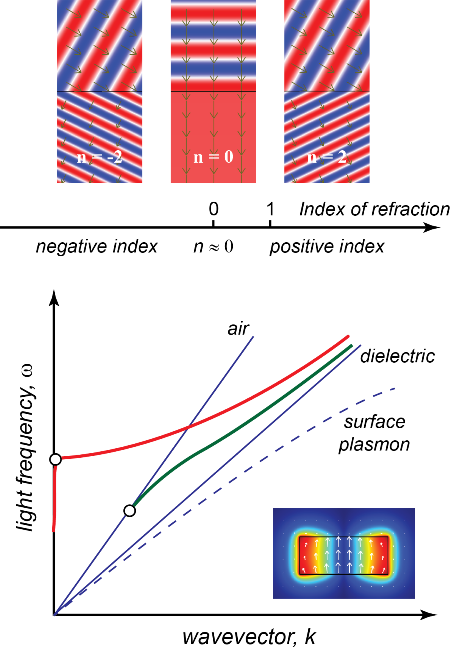
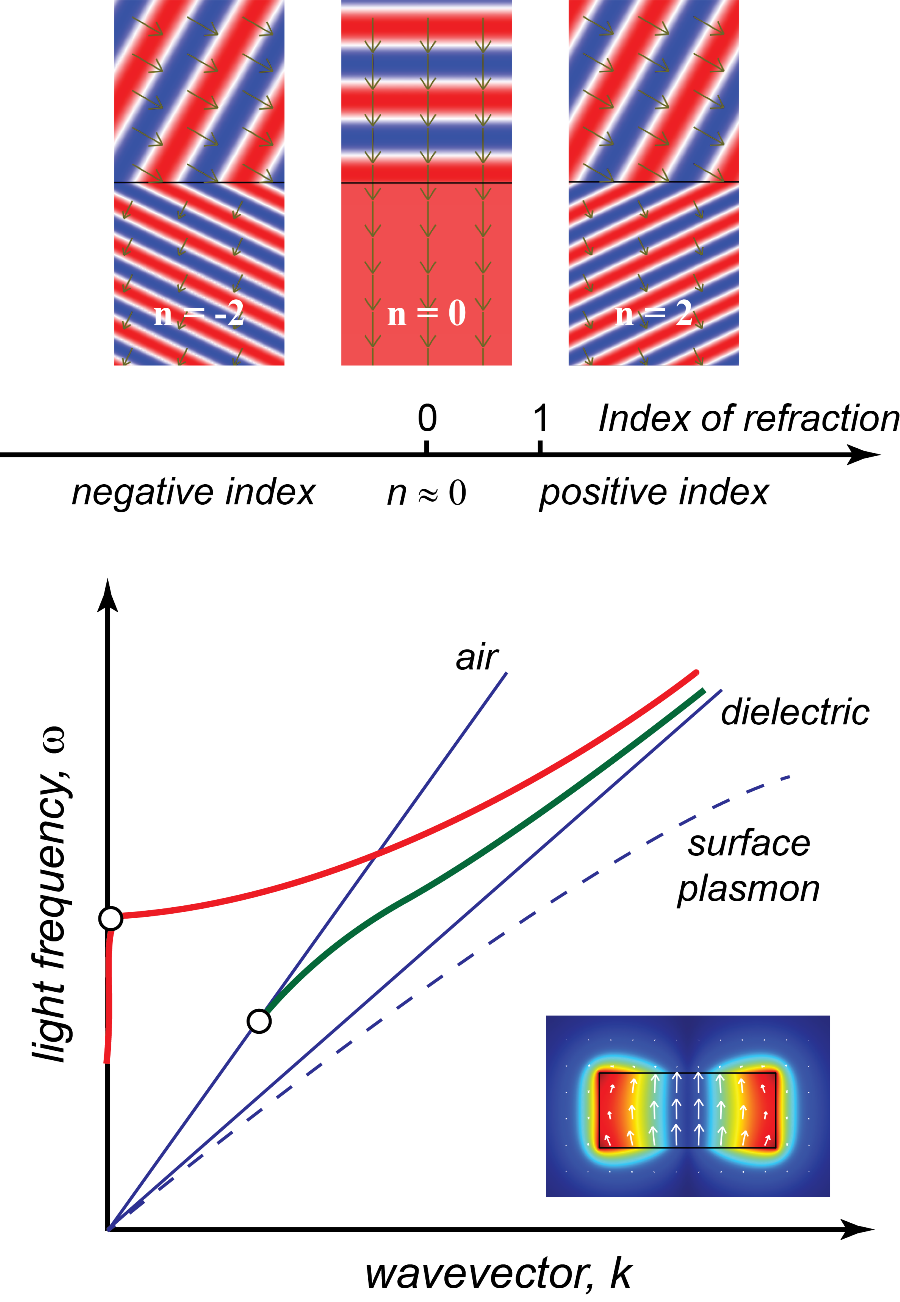
What we know about the index of refraction of various materials has progressed over many centuries. Early investigations into geometrical optics introduced this dimensionless quantity as a way to characterize the ability of a material to bend light rays, as described by Snell’s law. Later it was discovered that the refraction of light in an anisotropic material is direction sensitive, and in this situation the refractive index possesses the form of a tensor rather than a scalar value. With the development of wave optics, the refractive index is now recognized as a measure describing the reduction of the speed and wavelength of light compared to their free-space counterparts, following the simple relations $ν = c / n$ and $λ = λ_{0} / n$ . (The frequency $ω = 2 π c / λ_{0} = 2 π ν / λ$ doesn’t vary in a “linear” optical material.) In a general case where the wave has a propagation factor $e^{- i (ω t - k z)}$ , the refractive index (and consequently the wave vector $k = ω n / c$ ) assumes a complex value $n = n^{'} + i n^{''}$ , where $exp (i 2 π n^{'} z / λ_{0})$ describes the phase advance the wave acquires during its propagation, and $exp (- 2 π n^{''} z / λ_{0})$ gives the exponential decay of the field magnitude. The past decade has witnessed an explosive development of metamaterials, as researchers have striven to develop and utilize man-made materials with anomalous refractive indices, ranging from the negative to the infinite (Fig. 1, top), with exotic applications such as super-resolution lenses and invisibility cloaks [2].

Recently, growing attention has been devoted to materials with near-zero index of refraction, which are sometimes referred to as epsilon-near-zero (ENZ) materials due to the connection between the refractive index and the dielectric constant $n = \sqrt{ϵ}$ . Within an ENZ material, the wave exhibits little or no spatial variation, as the wavelength $λ = λ_{0} / n$ approaches infinity (see Fig. 1, top middle). In addition, the speed of light in the material, as indicated by $ν = c / n$ , becomes superluminal, posing an apparent contradiction to relativity. However, this velocity is the “phase velocity,” which describes the rate at which the phase of the wave propagates. In contrast, the optical power or information travels at the “group velocity,” which is limited by relativity, so causality still holds. To give a specific example, consider noble metals like silver or gold, whose conducting electrons can be approximated as an electron gas. In this case, the index of refraction is $n = \sqrt{1 - (ω_{p} / ω)^{2}}$ , where $ω_{p}$ is the so-called plasma frequency. Based on the definitions of the phase velocity $ν_{p} = ω / k$ and the group velocity $ν_{g} = d ω / d k$ , we obtain $ν_{p} = c / \sqrt{1 - (ω_{p} / ω)^{2}}$ and $ν_{g} = c \sqrt{1 - (ω_{p} / ω)^{2}}$ . Consequently, a zero index occurs at the plasma frequency, where $ν_{p} \to \infty$ and $ν_{g} \to 0$ . In general, any material with $| n | < 1$ will be dispersive (with the index of refraction depending on wavelength), and any modulated signal in the material will travel below the speed of light in vacuum, albeit with a superluminal phase velocity for certain frequencies.

Besides noble metals, other homogeneous materials may exhibit a near-zero index in a specific wavelength range, such as polar dielectrics, heavily doped semiconductors, and some metal oxides. Artificially structured materials also have a long history as a viable route to near-zero refractive index. Examples include a metallic wire mesh that mimics an electric plasma with tailored plasma frequency [3], stratified structures with alternating metallic and dielectric layers that provide an anisotropic ENZ medium, and metamaterials with resonant inclusions that allow impedance matching [4]. Moreover, the recent developments in negative-index metamaterials offer zero index as a by-product. The reasoning is as follows: all negative-index media are dispersive, and the refractive index is a continuous function of wavelength, so there must exist a frequency between the negative-index band and the (positive-index) nonresonant spectral range at which the effective index is exactly zero.

In the present work, Vesseur et al. demonstrate a near-zero index utilizing the cutoff frequency in a metallic (plasmonic) waveguide built at the nanoscale. The basic idea dates back to earlier microwave studies from half a century ago, but it has been revived very recently at optical frequencies [5]. An ENZ material in a waveguide configuration opens up many applications, such as subwavelength channel propagation [6]. The strategy takes advantage of the particular dispersion relation between frequency and wave vector in a metallic waveguide. A normal dielectric waveguide has a dispersion relation that cuts off at the point where it crosses the light line ( $ω / k = c / n$ ) of the low-index cladding medium (which is air in the example given in Fig. 1, bottom). Below this cutoff frequency, light leaks out of the waveguide. In contrast, a metallic hollow waveguide possesses a dispersion curve that starts near the light line of the embedded dielectric and ends at the vertical axis where $k = 0$ (Fig. 1, bottom). A vanishingly small wave vector at a nonzero frequency indicates a waveguide mode with near-zero index $n_{e f f} = k / k_{0}$ , as well as a phase velocity $ν_{p} = ω / k$ approaching infinity.

The waveguide used by Vesseur et al. has a rectangular glass core ( $85$ by $190$ nanometers), surrounded by a silver cladding on all sides. Embedding an emitting source inside an ENZ material can be challenging, but the researchers overcame this by using an electron beam to excite the plasmonic waveguide and thus probe the optical density of states. They observed the near-zero-index mode occurring near the far-red end of the visible spectrum, but they can potentially tune this wavelength by altering the dimensions of the dielectric slot. This tunability in the waveguides is a significant advantage over other ENZ materials, like noble metals and polar dielectrics, where the wavelength of zero index is fixed. There also exists the possibility of packing many of these waveguides together into an array to form a bulk metamaterial with a zero effective index [7].

A vanishing refractive index is certainly more than a mathematical trick. It enables far-reaching possibilities for both fundamental physics and exciting novel applications. The spatially uniform phase distribution (or vanishing phase advance) for the zero-index mode implies directed and enhanced radiation from emitters either embedded inside the medium [8], or externally excited as shown by Vesseur and coauthors. Potential applications of zero-index materials include arbitrary wave front design, supercoupling with subwavelength channels, air-core waveguides, innovative lenses, insulating media for optical lumped nanocircuits, and many more [9,10]. By stretching the wavelength of light at optical frequencies, zero-index materials provide an interesting contrast to surface plasmons, which have a flat dispersion relation (see Fig. 1, bottom) that shrinks light at optical frequencies down to x-ray wavelengths. Once again, the ever-evolving field of nanophotonics challenges our traditional understanding of optics, and offers unconventional means to manipulate light waves.

References

E. J. R. Vesseur, T. Coenen, H. Caglayan, N. Engheta, and A. Polman, “Experimental Verification of n=0 Structures for Visible Light,” Phys. Rev. Lett. 110, 013902 (2013)
W. Cai and V. M. Shalaev, Optical Metamaterials: Fundamentals and Applications (Springer, New York, 2010)[Amazon][WorldCat]
J. Brown, “Artificial Dielectrics Having Refractive Indices Less Than Unity,” Proc. IEEE 100, 51 (1953)
S. Yun, Z. H. Jiang, Q. Xu, Z. W. Liu, D. H. Werner, and T. S. Mayer, “Low-Loss Impedance-Matched Optical Metamaterials with Zero-Phase Delay,” ACS Nano 6, 4475 (2012)
W. Rotman, “Plasma Simulation by Artificial Dielectrics and Parallel-Plate Media,” IRE Trans. Antennas Propag. 10, 82 (1962)
M. G. Silveirinha and N. Engheta, “Theory of Supercoupling, Squeezing Wave Energy, and Field Confinement in Narrow Channels and Tight Bends Using Epsilon Near-Zero Metamaterials,” Phys. Rev. B 76, 245109 (2007)
S. P. Burgos, R. de Waele, A. Polman, and H. A. Atwater, “A Single-Layer Wide-Angle Negative-Index Metamaterial at Visible Frequencies,” Nature Mater. 9, 407 (2010)
S. Enoch, G. Tayeb, P. Sabouroux, N. Guerin, and P. Vincent, “A Metamaterial for Directive Emission,” Phys. Rev. Lett. 89, 213902 (2002)
M. Silveirinha and N. Engheta, “Tunneling of Electromagnetic Energy through Subwavelength Channels and Bends Using Epsilon-Near-Zero Materials,” Phys. Rev. Lett. 97, 157403 (2006)
N. Engheta, “Circuits with Light at Nanoscales: Optical Nanocircuits Inspired by Metamaterials,” Science 317, 1698 (2007)

About the Author

Wenshan Cai joined the faculty of Georgia Institute of Technology as an associate professor in January 2012. Prior to this, he worked as a postdoctoral fellow at Stanford University for three years after receiving his Ph.D. from Purdue University in 2008. His impact on the evolving field of plasmonics and metamaterials is exemplified by over 3,000 citations of his recent papers. He authored the book Optical Metamaterials: Fundamentals and Applications (Springer, 2010), which is used as a textbook or reference at many universities around the world. He leads the Laboratory for Advanced Photonics and Optoelectronics (LAPO) at Georgia Tech, which is focused on the design and implementation of nanophotonic materials and devices.