It’s a Good Time for Time-Bin Qubits
In contrast to classical bits of information that are either 0 or 1, quantum bits—or “qubits”—can be in superposition states of 0 and 1. Just like classical bits, however, qubits are physical objects that have to be implemented in real physical systems. Researchers have used single photons as physical qubits, with the quantum information encoded in terms of polarization, angular momentum, and many other degrees of freedom. The time-bin degree of freedom (that is, encoding quantum information in terms of relative arrival times of light pulses) offers a particularly robust kind of single-photon qubits, and two recent papers have advanced the use of time-bin qubits in dramatic ways.
Writing in Physical Review Letters, Peter Humphreys and colleagues at the University of Oxford, UK, have developed a technique for optical quantum computing using time-bin qubits [1]. In principle, their concept allows photonic quantum computing using a single optical path (or fiber) rather than a maze of multiple paths, thereby drastically reducing the overall complexity of these kinds of systems. Also in Physical Review Letters, John Donohue and colleagues at the Institute for Quantum Computing, University of Waterloo, Canada, have demonstrated an ultrafast measurement technique for time-bin qubits that could enable higher data rates and fewer errors in photonic systems [2]. These two developments represent a huge step towards the realization of practical quantum information processing devices using single-photon qubits.
Time-bin qubits were originally developed by a group at the University of Geneva, Switzerland [3]. To understand the basic form of these qubits, consider a single-photon wave packet passing through a two-path Mach-Zehnder interferometer: if the two paths have different lengths, the photon wave packet will exit the interferometer in a quantum-mechanical superposition of an “early time bin” and “later time bin.” By adjusting the parameters of the interferometer to control relative phase and amplitude, one can accurately produce arbitrary time-bin qubits. The Geneva group famously showed that these time-bin qubits could propagate over long distances in optical fibers with very little decoherence, allowing much more robust quantum communication systems than those based on polarization-encoded qubits [4,5].
Extending these ideas from the realm of quantum communication, Humphreys et al. have now shown that it is possible to use time-bin qubits for quantum computing [1]. Their approach is based on the well-known linear optics quantum computing (LOQC) paradigm that uses large numbers of ancilla photons and measurement-based nonlinearities to realize near-deterministic quantum logic gates [6]. Previous work on the LOQC approach has primarily been based on polarization qubits and spatial modes that can quickly escalate into extremely unwieldy nested interferometers with very large numbers of paths that need to be stabilized to subwavelength precision [6–8]. In contrast, Humphreys et al. have now shown that the use of time-bin qubits enables the LOQC approach in a single spatial mode, offering the possibility of far less experimental complexity and a potential for reduced decoherence mechanisms.
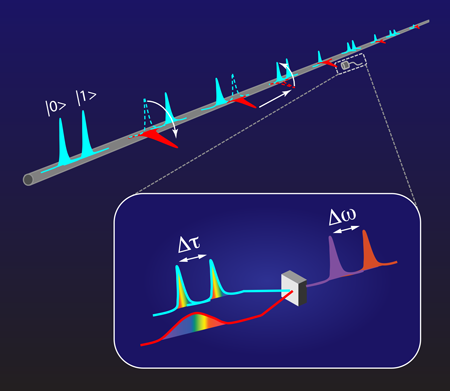
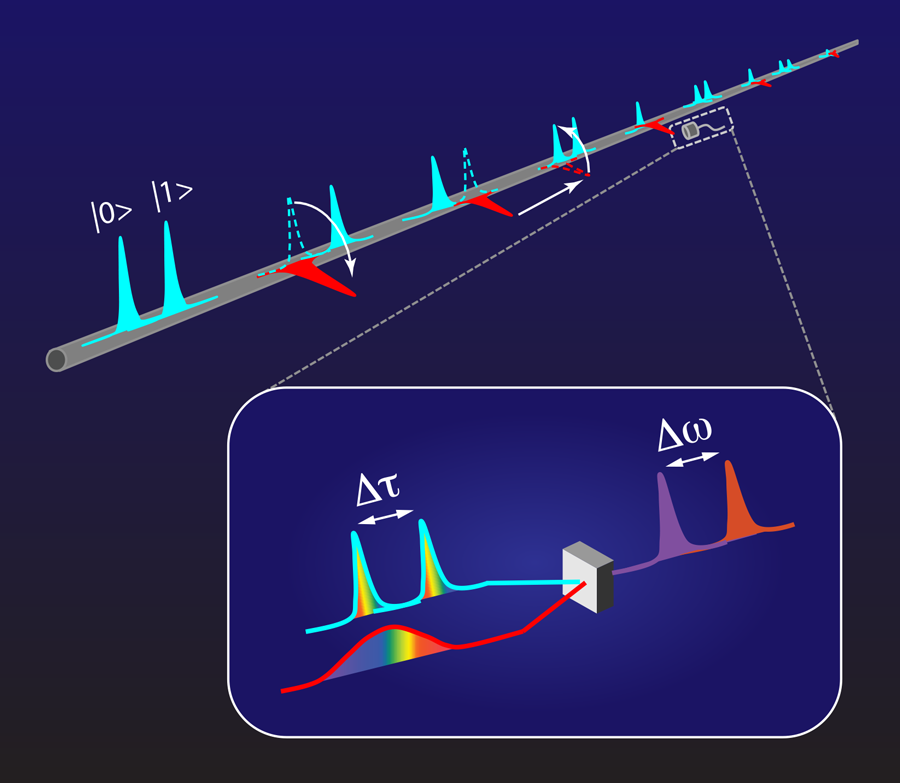
As shown in Fig. 1, their approach involves a large string of time-bin qubits propagating along a single waveguide (such as an optical fiber), with the available polarization degree of freedom used to define a “register” mode for propagation and storage, and a “processing” mode for qubit manipulations. As the qubits propagate along the waveguide, Humphreys et al. pull out various time bins from the register mode, process them with phase shifts, bit flips, and couplings, and then return them to the register mode in a coherent way. The authors used these ideas to propose the full suite of single-qubit operations and two-qubit entangling gates needed for universal quantum computation. The validity of their basic method was demonstrated in a very convincing experiment that used single-photon qubits and linear optical elements for time-bin creation and manipulation [1].
In any approach to quantum information processing, one of the key requirements is the ability to measure arbitrary qubit states. For the time-bin qubits discussed here, this turns out to mean that the separation between the “early” and “late” time bins has to be much greater than the resolution time of the photon detection system being used. With commercially available devices, this typically requires nanosecond-scale separation of the time bins and limits the effective “data rate” for sending time-bin qubits down a quantum channel. Using a radical departure from traditional time-bin qubit detection techniques, Donohue et al. have now pushed this number down to the picosecond scale, offering the potential for much higher information density [2].
The approach of Donohue et al. is essentially a clever method for coherently converting time bins into “frequency bins” that can be easily measured with slow detectors—even when the time bins are pushed arbitrarily close together. As illustrated in the inset to Fig. 1, this time-to-frequency conversion is based on qubit frequency conversion techniques that mix a single-photon qubit with an auxiliary strong laser pulse in a nonlinear medium [9]. By oppositely “chirping” the qubit and strong laser signals (i.e., stretching them so that their frequencies vary oppositely in time—like mirror-image rainbows), the authors were able to show that the time-bin information maps perfectly into corresponding frequency bins. The real power of the technique—the ability to make measurements of arbitrary time-bin qubits—arises when the auxiliary laser pulse is also put into a superposition of time bins. Using this approach, Donohue et al. were able to experimentally demonstrate ultrafast measurements on arbitrary time-bin states [2].
The next steps for moving these two new promising ideas from the research lab towards “practical quantum information processing devices” will be of a more technical nature. For Humphrey’s time-bin LOQC approach, this simply means an emphasis on improving the efficiency of the photonics technologies (switches, phase shifters, etc.) needed, while for Donohue’s ultrafast time-bin qubit detectors, it means improving the efficiency of the time-to-frequency conversion process. Combining these ideas with other recent advances in photonic quantum information processing is also an exciting prospect. For example, chip-based devices have recently demonstrated remarkable stability [10], and a hybrid scheme involving several spatial modes with Humphrey’s temporal methods [1] and Donohue’s ultrafast detection scheme [2] may enable near-term realizations of quantum circuits with more than “a few” single-photon qubits.
References
- P. C. Humphreys, B. J. Metcalf, J. B. Spring, M. Moore, X-M. Jin, M. Barbieri, W. S. Kolthammer, and I. A. Walmsley, “Linear Optical Quantum Computing in a Single Spatial Mode,” Phys. Rev. Lett. 111, 150501 (2013)
- J. M. Donohue, M. Agnew, J. Lavoie, and K. J. Resch, “Coherent Ultrafast Measurement of Time-Bin Encoded Photons,” Phys. Rev. Lett. 111, 153602 (2013)
- J. Brendel, N. Gisin, W. Tittel, and H. Zbinden, “Pulsed Energy-Time Entangled Twin-Photon Source for Quantum Communication,” Phys. Rev. Lett. 82, 2594 (1999)
- I. Marcikic, H. de Riedmatten, W. Tittel, H. Zbinden, M. Legré, and N. Gisin, “Distribution of Time-Bin Entangled Qubits over 50 km of Optical Fiber,” Phys. Rev. Lett. 93, 180502 (2004)
- J. D. Franson, “Bell Inequality for Position and Time,” Phys. Rev. Lett. 62, 2205 (1989)
- E. Knill, R. LaFlamme, and G. J. Milburn, “A Scheme for Efficient Quantum Computation with Linear Optics,” Nature (London) 409, 46 (2001)
- T. B. Pittman, M. J. Fitch, B. C. Jacobs, and J. D. Franson, “Experimental Controlled-NOT Logic Gate for Single Photons in the Coincidence Basis,” Phys. Rev. A 68,032316 (2003)
- J. L. O’Brien, G. J. Pryde, A. G. White, T. C. Ralph, and D. Branning, “Demonstration of an All-Optical Quantum Controlled-NOT Gate,” Nature (London) 426, 264 (2003)
- J. Huang and P. Kumar, “Observation of Quantum Frequency Conversion,” Phys. Rev. Lett. 68, 2153 (1992)
- A. Politi, M. J. Cryan, J. G. Rarity, S. Yu, and J. L. O’Brien, “Silica-on-Silicon Waveguide Quantum Circuits,” Science 320, 646 (2008)