Ion Pair Simulates Hybrid Excitations
Nature presents us with a tremendous variety of quantum-mechanical systems, and a great deal of current research aims at mapping their behavior. In many of these systems, the microscopic dynamics are experimentally inaccessible, so one must try to infer the underlying microscopic behavior by creating theoretical models that predict the complex macroscopic behavior. However, making these predictions requires great effort in itself. By contrast, certain quantum systems are well characterized both microscopically and macroscopically, and extensive research on them allows a high level of control over their behavior. With the development of these “tamed” quantum entities, one can now experimentally realize a wide variety of quantum models in a single system, a technique called quantum simulation. To date, quantum simulators made from ultracold atoms, ions, or photons have reproduced complex phenomena in many-body condensed matter and relativistic physics [1]. A new quantum simulation experiment [2] performed by Kenji Toyoda and colleagues of Osaka University in Japan uses trapped ions to simulate polaritons, which are hybrid quasiparticles that combine excitation of an electromagnetic polarization wave and a mechanical vibration wave. As described in Physical Review Letters, this is the first realization of a particular microscopic model for a superfluid-insulator phase transition common in condensed-matter physics.
Uniquely among current experimental implementations of quantum simulation, trapped ions can simulate the evolution of highly nonequilibrium systems and permit measurement of any desired observable or correlation function. Over the past 20 years, a complete toolbox for quantum manipulation of ions has been developed in efforts toward quantum computing [3]. These tools are readily repurposed to give the maximum flexibility in a quantum simulator. However, executing an ion-based simulation requires full and independent control of every relevant quantum degree of freedom, and many auxiliary ones, which is why these experiments have so far only incorporated 16 ions or fewer [4]. These advantages and disadvantages are almost exactly complementary to the other major quantum simulation platform, based on neutral atoms, which employs thousands of particles but is, so far, restricted in its dynamics and measurement capabilities.
The Bose-Hubbard model is perhaps the most thoroughly investigated target of quantum simulation experiments, as it is closely related to the tight-binding model underlying much of condensed-matter physics. In Bose-Hubbard, a lattice of sites is populated by many bosons. A repulsive potential deters bosons from occupying the same site, while a nearest-neighbor coupling permits tunneling of bosons between sites. Previous quantum simulations using neutral atoms have observed the major prediction of the model: a quantum phase transition between insulating and superfluid states induced by changes to the strength of the tunneling [5]. Such superfluid-insulator transitions are commonly observed in systems like liquid helium films and disordered superconductors.
The Bose-Hubbard model can be extended to give each site a fermionic “spin” mode as well as the bosonic mode. At each site, the boson and spin modes can exchange excitation according to the Jaynes-Cummings coupling, which may be most familiar as the textbook description of fully quantized absorption and emission of photons by matter. The coupled spin-boson system, referred to as the Jaynes-Cummings-Hubbard (JCH) model, naturally produces hybrid spin-boson modes, or polaritons, that are akin to polaritons found in semiconductor quantum wells and microcavities. The JCH model is also found to exhibit other exotic phenomena of condensed-matter physics, such as topological excitations and fractional quantum Hall physics [6].
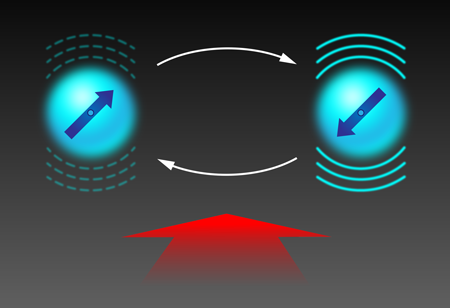
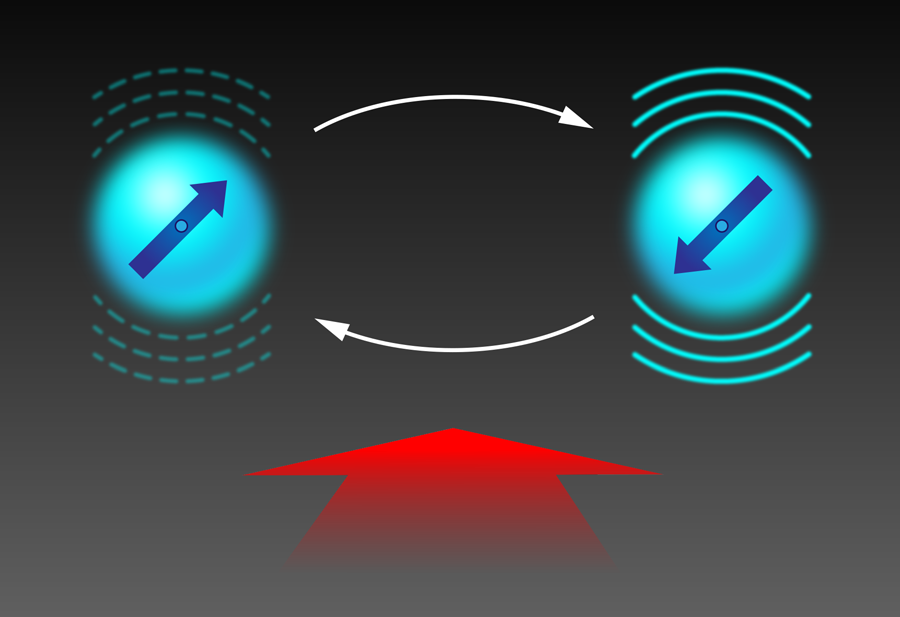
While the JCH model has provoked extensive theoretical discussion, it has not previously been realized in any experimental system. Now, the Osaka University group, led by Shinji Urabe, has simulated the JCH model using a “crystal” of trapped ions [2]. Using a combination of radiofrequency and static electric fields, the team confined two calcium ions within 20 micrometers of each other. Each ion represents a single lattice site, and the quantized vibration of an ion within the trapping potential represents the boson mode at the site. Each ion also possesses two long-lived electronic states, representing the spin mode at the site (see Fig. 1). The Jaynes-Cummings coupling between vibrational and electronic modes arises naturally from laser driving of the long-lived electronic transition, as is well known from quantum information experiments. Following a recent proposal [7], Toyoda et al. selected vibrational modes that can be regarded as well localized to individual ions, but which can be driven to tunnel between ions using the same laser interaction that produces the Jaynes-Cummings coupling. The relative simplicity of the laser interactions makes the simulator straightforward and robust.
In a first set of experiments, Toyoda et al. demonstrate that the physics of their simulator is best characterized in terms of polaritons, as expected from the theory of the JCH model. The researchers employ laser cooling to initialize the simulator in the ground state, for which both spin and boson excitations are absent. Then they make a slight tweak to the laser couplings to create a state with exactly two excitations: both spin modes are excited but the boson modes stay in their ground states. However, excitations can transfer from spin to boson modes and vice versa. The researchers observed this time-dependent energy exchange in periodic, high-contrast revivals of the spin excitation. The strong spin-boson coupling and conservation of total (spin + boson) excitation number indicate that the eigenstates of the system are actually spin-boson hybrid excitations, i.e., polaritons.
Toyoda et al. then press on to observe the fundamental phase transition of the JCH model, in which the polaritons transition from an insulating to a superfluid state. Using the same initialization procedure as before, they create a two-excitation state in the insulating part of the phase diagram, where the excitations are well localized. The strength of the Jaynes-Cummings coupling is kept low, so that the polaritons are almost exclusively spin excitations and the bosonic sector remains in the ground state. Now, tuning the drive laser frequency increases both the Jaynes-Cummings coupling and the bosonic hopping rate. The polaritons are converted to bosonic excitations, and at the same time, the insulating phase melts into a superfluid. The complete control afforded by the quantum simulator allows the team to map out the transition at several different points on the phase diagram. Toyoda et al. measure not only the mean excitation of the spin and boson modes during the phase transition, but also their variances, using techniques developed for quantum information processing. As expected, the variance in both modes is low in the insulating phase, but the boson variance increases at the superfluid transition, indicating delocalization of the polaritons.
The challenge ahead for these experiments, like most trapped-ion quantum simulators, is to increase the number of particles in the simulation. Toyoda et al. have made a promising first step: the techniques they use are scalable to tens or hundreds of ions with little modification. This increased simulator size should present a sharper insulator/superfluid phase transition with strongly correlated states arising near the transition. The flexible techniques of trapped-ion simulators can probe entanglement dynamics of these states as well as the evolution of the model under strong driving and dissipation. Observing the details of such a highly nonequilibrium, strongly correlated system will undoubtedly provoke new insights into its cousins in other realms of physics.
References
- Nature Physics Insight - Quantum Simulation 8, No. 4 (2012)
- K. Toyoda, Y. Matsuno, A. Noguchi, S. Haze, and S. Urabe, “Experimental Realization of a Quantum Phase Transition of Polaritonic Excitations,” Phys. Rev. Lett. 111, 160501 (2013)
- J. P. Home et al., “Complete Methods Set for Scalable Ion Trap Quantum Information Processing,” Science 325, 1227 (2009)
- B. Lanyon et al., “Universal Digital Quantum Simulation with Trapped Ions,” Science 334, 57 (2011); R. Islam et al., “Emergence and Frustration of Magnetism with Variable-Range Interactions in a Quantum Simulator,” 340, 583 (2013)
- D. Jaksch, C. Bruder, J. I. Cirac, C. W. Gardiner, and P. Zoller, “Cold Bosonic Atoms in Optical Lattices,” Phys. Rev. Lett. 81, 3108 (1998); M. Greiner, O. Mandel, T. Esslinger, T. W. Hänsch, and I. Bloch, “Quantum Phase Transition from a Superfluid to a Mott Insulator in a Gas of Ultracold Atoms,” Nature 415, 39 (2002)
- M. J. Hartmann, F. G. S. L. Brandão, and M. J. Plenio, “Strongly Interacting Polaritons in Coupled Arrays of Cavities,” Nature Phys. 2, 849 (2006); A. D. Greentree, C. Tahan, J. H. Cole, and L. C. L. Hollenberg, “Quantum Phase Transitions of Light,” 2, 856 (2006); A. L. C. Hayward, A. M. Martin, and A. D. Greentree, “Fractional Quantum Hall Physics in Jaynes-Cummings-Hubbard Lattices,” Phys. Rev. Lett. 108, 223602 (2012)
- P. A. Ivanov et al., “Simulation of a Quantum Phase Transition of Polaritons with Trapped Ions,” Phys. Rev. A 80, 060301 (2009)