How to Control Your Dragons
Every decision maker would rejoice if given the ability to predict and control extreme events—financial crises, environmental accidents, earthquakes, power outages, and the like. But the complex systems (natural or man-made) prone to such events still defy our understanding. The behavior of these systems—often described as networks of interconnected units—cannot be inferred from the properties of their parts. One of their common traits is that local events can have far-reaching consequences that are often difficult to anticipate. Carefully designed power grids, for example, may exhibit predictable behavior close to their normal modes of operation. But certain events can drive them away from such modes, leading to large-scale flow rearrangements and possibly to large power outages. A perturbed power grid often poses operational challenges for which no general solutions currently exist. A similar knowledge gap applies to virtually all complex systems. The difficulty has its origin in our inability to understand how seemingly ordinary events give rise to extreme ones. This lack of understanding has hampered progress and led to the tacit assumption that, once initiated, large-scale failures are unstoppable. As reported in Physical Review Letters, Hugo de S. Cavalcante at the Federal University of Paraíba, Brasil, and his collaborators built a model system made of coupled electrical oscillators to demonstrate that certain types of extreme events can be predicted early enough that they can be suppressed by means of gentle control interventions [1].
There are in principle two broad approaches to mitigate extreme events and large-scale failures in general. The first approach works by engineering and/or maintaining the system in such a way as to prevent the triggering of potentially harmful large-scale events. This should certainly be done, but it cannot realistically prevent all failures. The second approach is focused on developing tools to prevent the amplification and propagation of those events whose triggering could not be prevented, so that small events remain small. A priori network optimization (e.g., designing a resilient power grid) is an example of the first, while real-time cascade control (e.g., preventing the spread of a blackout) is an example of the second. The latter of these two approaches is gaining momentum with the recent development of techniques to control complex systems in the presence of an impeding extreme event [2] that might have been triggered by an external perturbation. Now, the work of Cavalcante et al. [1] illustrates that in a chaotic system large-scale events can be caused not only by external perturbations but also through a phenomenon known as bubbling [3] and, moreover, that bubbling events can be controlled individually as they start to emerge.
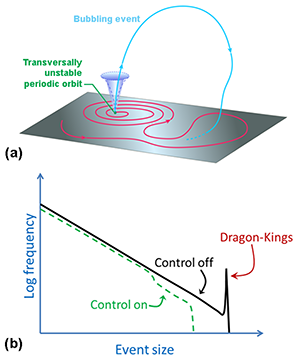
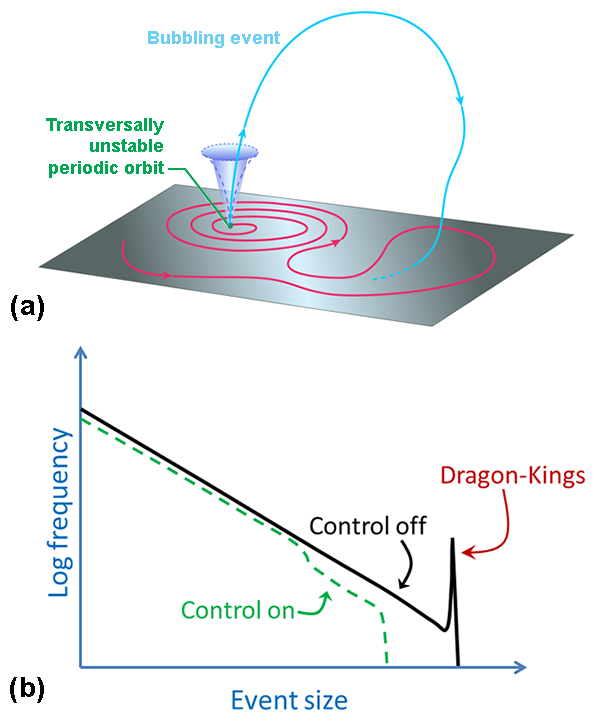
Bubbling can occur when trajectories close to a chaotic attractor undergo rare but pronounced excursions away from it. At first, this may seem surprising since attractors are, by definition, invariant sets of orbits representing the asymptotic behavior of the nearby trajectories they attract. For a large class of attractors, noise, which is unavoidable in realistic situations, will not change the qualitative properties of typical trajectories. But for other attractors, even low-intensity noise can have dramatic implications. This can occur when the attractor exists in a surface (a hyperplane, say) of the phase space and one or more of the periodic orbits embedded in the attractor are unstable in the direction transverse to the surface [Fig. 1(a)]. In the absence of noise, the trajectories of the attractor remain in the attractor forever. In the presence of noise, however, when they visit a neighborhood sufficiently close to one of these periodic orbits, they are ejected transversely to the attractor’s surface. Such visits (and hence bubbling events) are expected because of the ergodicity of chaotic attractors, according to which typical orbits of an attractor pass arbitrarily close to any of its points, including any transversely unstable ones.
The ejected trajectory may subsequently return to the attractor, after undergoing a brief but large excursion far away from it (thus bubbling can, in principle, occur even in a system with a single global attractor). This is the scenario considered in Ref. [1], where they studied experimentally an electric circuit formed by two coupled chaotic oscillators. The attractor corresponds to a state in which the two oscillators are synchronized. The bubbling events lead to periods of desynchronization and are the extreme events of interest. A first important observation in Ref. [1] is that the frequency distribution of event sizes follows an approximate power-law distribution for small and intermediate size events but exhibits a pronounced peak for large events associated with bubbling [Fig. 1(b), solid line]. The outliers in the curve’s peak are identified by the authors as “dragon kings,” following the definition of previous studies [4]: large-scale events (kings) that belong to a completely different species (dragons). Since they originate via distinct mechanisms, dragon kings can be predicted—at least in principle.
In their experiments, the authors were able to identify early signs of a bubbling event from changes in the dynamical variables (related to the measured electrical signals) that indicated the approach to a transversely unstable orbit. To mitigate the imminent extreme event they then implemented countermeasures through a feedback control method that redirected the trajectory toward the synchronization surface. The results show that this approach has marginal impact on the incidence of small events but strongly inhibits large ones [Fig. 1(b), dashed line]. Importantly, this selective mitigation of extreme events can be achieved with control perturbations that are both very small and of short duration. The challenge of identifying early signs of extreme events has much to do with our ability to model or observe the dynamics of the system [5]. In the case of bubbling, this is facilitated by the unique nature of the extreme events, which are statistically and mechanistically different from the power-law distributed nonbubbling events.
This is not to say that one cannot mitigate events with a power-law distribution of sizes. For example, Ref. [6] illustrates the potential of proactively triggering small cascades to prevent the building up of large ones in models of self-organized criticality. However, the lack of a distinct mechanistic origin can make it more challenging to anticipate the consequences of individual interventions and to identify the events that should be suppressed [7].
The control approach proposed by Cavalcante et al. is most immediately applicable to systems that are recurrent, where repeated extreme events can be observed (or accurately modeled). The concept has the potential to be broadly relevant as there has been evidence of dragon kings in diverse contexts, ranging from fluid dynamics to neuronal networks [8]. On the other hand, extreme events of massive proportions are often extremely rare and do not offer opportunity for repeated experimentation—for instance, potentially irreversible changes in the state of the Earth’s climate and biosphere. A significant effort to study such phenomena has focused on predicting regime shifts induced by bifurcations, in which qualitative changes in behavior are due to changes in the system itself (see, e.g., Ref. [9]). Developing approaches to expand the class of rare extreme events that can be predicted and controlled is an important challenge for future research. The recognition of bubbling as a scenario for extreme events—a possibility not yet widely appreciated—is thus one of the important contributions of Cavalcante et al.’s work.
References
- H. L. D. de S. Cavalcante, M. Oriá, D. Sornette, E. Ott, and D. J. Gauthier, “Predictability and Suppression of Extreme Events in a Chaotic System,” Phys. Rev. Lett. 111, 198701 (2013)
- S. P. Cornelius, W. L. Kath, and A. E. Motter, “Realistic Control of Network Dynamics,” Nat. Commun. 4, 1942 (2013)
- P. Ashwin, J. Buescu, and I. Stewart, “Bubbling of Attractors and Synchronisation of Chaotic Oscillators,” Phys. Lett. A 193, 126 (1994); J. F. Heagy, T. L. Carroll, and L. M. Pecora, “Desynchronization by Periodic Orbits,” Phys. Rev. E 52, R1253 (1995)
- D. Sornette, “Dragon-Kings, Black Swans and the Prediction of Crises,” Intl. J. Terraspace Sci. Eng. 2, 1 (2009); arXiv:0907.4290
- Y. Yang, J. Wang, and A. E. Motter, “Network Observability Transitions,” Phys. Rev. Lett. 109, 258701 (2012); Y.-Y. Liu, J.-J. Slotine, and A.-L. Barabási, “Observability of Complex Systems,” Proc. Natl. Acad. Sci. USA 110, 2460 (2013)
- D. O. Cajueiro and R. F. S. Andrade, “Controlling Self-Organized Criticality in Sandpile Models,” Phys. Rev. E 81, 015102 (2010)
- P.-A. Noël, C. D. Brummitt, and R. M. D’Souza, “Controlling Self-Organizing Dynamics on Networks Using Models that Self-Organize,” Phys. Rev. Lett. 111, 078701 (2013)
- D. Sornette and G. Ouillon, “Dragon-Kings: Mechanisms, Statistical Methods and Empirical Evidence,” Eur. Phys. J. Special Topics 205, 1 (2012)
- A. D. Barnosky et al., “Approaching a State Shift in Earth’s Biosphere,” Nature 486, 52 (2012)