Clearing Up the Mysteries of Glassy Dynamics

Giulio Biroli; Jean-Philippe  Bouchaud

Viewpoint

Clearing Up the Mysteries of Glassy Dynamics

Giulio Biroli

IPhT, CEA/DSM-CNRS/URA 2306, CEA Saclay, F-91191 Gif-sur-Yvette Cedex, France

Jean-Philippe Bouchaud

Capital Fund Management, 23 rue de l’Université, Paris, France

November 25, 2013• Physics 6, 128

Measurements of nonlinear dielectric responses reveal the cooperative nature of the dynamics in fragile glasses.

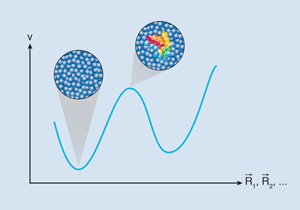
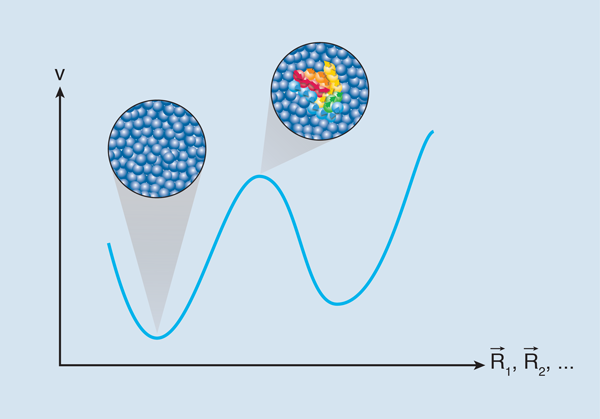
Figure caption — **Figure 1:** Sketch of a cooperative rearranging region in a glass and the part of the energy landscape related to it. The curve shows schematically the potential energy $V$ as a function of ${\vec{R}}_{1}$ , ${\vec{R}}_{2}, . . .,$ which are generalized coordinates indicating molecular positions. Blue indicates immobile molecules and red the most mobile ones. The arrows are in the direction of motion. The figure shows in a pictorial way that since more molecules have to move cooperatively approaching the glass transition, the associated effective energy barrier grows and the range of dynamic correlations increases. Bauer *et al.* [3] have measured these correlations as a function of temperature and have related them to the effective energy barriers, confirming this cooperative behavior for several different glass formers.

You might think all glasses are the same—that they are all viscous amorphous materials somewhere between solids and liquids. In fact, many glass-forming liquids fall into two categories: “strong” and “fragile.” As the temperature $T$ is reduced, the viscosity of strong glasses like ${SiO}_{2}$ increases as exp( $Δ / T$ ), where $Δ$ can be thought of as an energy barrier that particles have to overcome in order to move (Fig. 1). For fragile glasses, glucose for example, the increase of viscosity is even steeper, as if the effective energy barrier $Δ$ itself increases when the temperature is lowered.

Fifty years ago, Gerold Adam and Julian Gibbs [1] proposed an explanation of the growth of $Δ$ in terms of the increasingly cooperative nature of the molecular rearrangements needed for the liquid to flow. Since more molecules must unlock simultaneously at lower temperatures, the associated energy barrier should be larger. Although the Adam-Gibbs picture (or its more modern incarnation [2] ) accounts reasonably well for a host of experimental results on glass-forming liquids, a direct experimental proof of the relation between increased energy barriers and increased cooperativity has remained elusive. Establishing such a relation is crucial to give a firm basis to our current understanding of the physics of glasses and could help in imagining new, high-performance materials.

Now, the work of Thomas Bauer and colleagues at the University of Augsburg, Germany, reported in Physical Review Letters [3] could provide the missing link. Building upon earlier work by ourselves and our Saclay colleagues [4], Bauer et al. have estimated the temperature dependence of the number of dynamically correlated molecules in four glass-forming liquids: three fragile and one strong. They demonstrate that this number increases in much the same way as the effective energy barrier $Δ$ , precisely as Adam and Gibbs would predict. The trick—easier said than done—is to measure the frequency-dependent, nonlinear dielectric response of these liquids. It turns out that the deviations from linear behavior are directly proportional to the number of collectively rearranging molecules.

Bauer et al. achieve these results with a high-voltage frequency response analyzer: they place the samples between electrodes that subject the glasses to frequencies reaching $100$ kilohertz and voltages as high as $2000$ volts. From the impedance response at difference frequencies and temperatures, the researchers can map out the nonlinear susceptibility of the material. These measurements are very difficult because probing nonlinear responses requires such high electric fields, so high in fact that the experimental apparatus becomes unreliable. This adds a contribution that masks the signal produced by the sample, unless special care is devoted to remove it.

Why, then, should one go to the pain of measuring a nonlinear response function, rather than the much more congenial and well-studied linear dielectric response? This is where the very peculiar nature of fragile glasses, with which theorists are still wrestling, comes into play. A glass is, for all practical purposes, rigid, but with no apparent long-range order—glasses are just like liquids except they cannot flow. In the case of ordinary solids, we understand the appearance of rigidity: the liquid undergoes a first-order phase transition towards a state of broken symmetry characterized by a periodic arrangement of the particles.

In physical terms, long-range crystalline order means we can pull a solid at one end and make all the atoms move together. For strong glasses, rigidity is a mere question of time scales—it takes each atom a time of the order of exp( $Δ / T$ ) to escape its initial position, and this time becomes enormous at small temperatures. But for fragile glasses, the quandary is the additional growth of $Δ$ with temperature, suggesting that the system becomes locally rigid, in the sense that individual particles no longer move alone, as happens in ordinary solids. How can this be, since no symmetry appears to be broken?

The answer might come from our understanding of spin-glasses, i.e., disordered magnetic alloys that display a genuine phase transition between a paramagnetic, high-temperature phase, and a spatially ordered, but magnetically amorphous phase at low temperatures [5]. What is unusual about this transition is that a single snapshot of the orientation of the spins cannot reveal whether the system is above or below the transition temperature. In more technical terms, this means that the spin-spin correlation function does not reveal any singularity at the transition, because spins freeze in random directions. From this, we find that the usual response of the material to a magnetic field, called the linear magnetic susceptibility, is not singular either.

Despite all of this, some strange kind of amorphous order does set in below the transition, and the system indeed becomes magnetically rigid. What was understood more than 30 years ago is that the appearance of amorphous order is in fact accompanied by the divergence of the nonlinear magnetic susceptibility, which is sensitive to the existence of persistent spin-spin correlations, but not to their sign. This quantity therefore does not vanish upon averaging and turns out to be directly related to the length scale over which “amorphous magnetic order” is able to propagate.

The question is whether a similar scenario holds for glasses as well [2,6]. Amorphous order would set in over a certain length scale, corresponding to locally rigid, “well-packed” configurations of molecules that cannot move individually but only collectively. Still, these configurations look very much like those of the liquid, and higher-order correlation/response functions are again needed to elicit the presence of this “hidden” order, just as in spin-glasses [7]. The nonlinear dielectric susceptibility investigated in Saclay for glycerol [4] and in Augsburg for four different glasses [4], is but one of them, and these experiments do indeed confirm the growth of a cooperative length scale as glasses get more viscous (see also Refs. [8,9] for earlier, less direct hints).

However, whereas the spin-glass transition temperature is within experimental reach and indeed corresponds to a divergence of the nonlinear susceptibility, glasses fall out of equilibrium much before the putative “ideal glass” transition can be reached, precisely because the energy barriers themselves grow with temperature, leading to a spectacular slowing down as the system is cooled by only a few degrees. Instead of a true divergence, one rather expects the nonlinear dielectric constant to show a mildly growing peak at finite frequency (corresponding to the inverse relaxation time of the glass-forming liquid). This is precisely what is seen in the previous experiments [3] and in the new work by Bauer et al. [4]: the growth of the number of dynamically correlated molecules is by a factor of $2$ at most, but since the energy barrier $Δ$ is found to grow similarly, the relaxation time soon becomes much too large for the system to equilibrate.

In a sense, the prediction of Adam and Gibbs is self-defeating. It is inherently impossible to test in an asymptotic sense, since large cooperative lengths necessarily correspond to astronomical time scales. We might have to satisfy ourselves with the kind of comparative evidence provided by the Augsburg group [3], or else venture into nonequilibrium, aging phenomena, studied through the lens of nonlinear response functions [10], or we need to force the system towards the ideal glass transition by pinning some of the particles [11,6] (which is also some kind of very nonlinear response). Nonlinear responses still have much to reveal: the study of rejuvenation and memory in glassy systems, using nonlinear probes has not been attempted yet. This would allow one to interpret these fascinating effects in terms of a time-dependent cooperative length scale and possibly provide interesting new pieces of information about the existence of a spin-glass transition in a nonzero magnetic field [7], which is one of the remaining, hotly debated issue in condensed-matter physics.

References

G. Adam and J. H. Gibbs, “On the Temperature Dependence of Cooperative Relaxation Properties in Glass-Forming Liquids,” J. Chem. Phys. 43, 139 (1965)
T. Kirkpatrick, D. Thirumalai, and P. Wolynes, “Scaling Concepts for the Dynamics of Viscous Liquids near an Ideal Glassy State,” Phys. Rev. A 40, 1045 (1989)
T. Bauer, P. Lunkenheimer, and A. Loidl, “Cooperativity and the Freezing of Molecular Motion at the Glass Transition,” Phys. Rev. Lett. 111, 225702 (2013)
C. Crauste-Thibierge, C. Brun, F. Ladieu, D. L’Hôte, G. Biroli, and J.-P. Bouchaud, “Evidence of Growing Spatial Correlations at the Glass Transition from Nonlinear Response Experiments,” Phys. Rev. Lett. 104, 165703 (2010)
See, e.g., K. Binder, and A. P. Young, “Spin Glasses: Experimental Facts, Theoretical Concepts, and Open Questions,” Rev. Mod. Phys. 58, 801 (1986)
J.-P. Bouchaud and G. Biroli, “On the Adam-Gibbs-Kirkpatrick-Thirumalai-Wolynes Scenario for the Viscosity Increase in Glasses,” J. Chem. Phys. 121, 7347 (2004)
J.-P. Bouchaud and G. Biroli, “Nonlinear Susceptibility in Glassy Systems: A Probe for Cooperative Dynamical Length Scales,” Phys. Rev. B 72, 064204 (2005)
L. Berthier, G. Biroli, J.-P. Bouchaud, W. Kob, K. Miyazaki, and D. R. Reichman, “Spontaneous and Induced Dynamic Fluctuations in Glass Formers. I. General Results and Dependence on Ensemble and Dynamics,” J. Chem. Phys. 126, 184503 (2007); L. Berthier, G. Biroli, J.-P. Bouchaud, L. Cipelletti, D. El Masri, D. L’Hôte, F. Ladieu, and M. Pierno, “Direct Experimental Evidence of a Growing Length Scale Accompanying the Glass Transition,” Science 310, 1797 (2005)
M. Ediger, “Spatially Heterogeneous Dynamics in Supercolled Liquids,” Ann. Rev. Phys. Chem. 51, 99 (2000)
C. Brun, F. Ladieu, D. L’Hôte, G. Biroli, and J.-P. Bouchaud, “Evidence of Growing Spatial Correlations during the Aging of Glassy Glycerol,” Phys. Rev. Lett. 109, 175702 (2012)
C. Cammarota and G. Biroli, “Ideal Glass Transitions by Random Pinning,” Proc. Natl. Acad. Sci. U.S.A. 109, 8855 (2012)

About the Authors

Giulio Biroli earned his Ph.D. in physics in 2000 from the Ecole Normale Supérieure in Paris. After two years of postdoctoral research in the condensed-matter theory group at Rutgers University, he joined the Institute of Theoretical Physics at CEA-Saclay as a permanent member. He is a theoretical physicist working on soft and hard condensed matter and statistical physics. For his studies on the thermodynamics and dynamical properties of the glass transition and jamming phenomena, he received the Young Scientist award in Statistical Physics 2007 from the IUPAP. Since 2007 he has been director and organizer of the Beg Rohu summer school of physics.

Jean-Philippe Bouchaud graduated from the Ecole Normale Supérieure in Paris, where he also obtained his Ph.D. in physics in 1985. Until 1992, he held an appointment with the CNRS. After a year spent in the Cavendish Laboratory (Cambridge), he joined the Service de Physique de l’Etat Condensé (CEA-Saclay), where he worked on the dynamics of glassy systems and on granular media. Bouchaud became interested in economics and theoretical finance in 1991. His work in finance includes extreme risk models, agent based simulations, market microstructure, and price formation. He founded the company Science & Finance in 1994 that merged with Capital Fund Management (CFM) in 2000, and was appointed as a Statistical Physics Professor at ESPCI (Paris) in 2000, a position he held for 8 years. He is now the Chairman and Head of Research at CFM, and professor at Ecole Polytechnique where he teaches statistical mechanics and a course on “complex systems.” In 2009 he was recognized as an Outstanding Referee by the American Physical Society.