Tales of 1001 Atoms
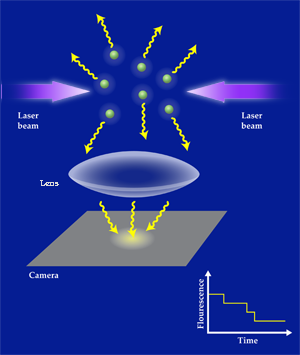
Imagine trying to count grains of rice in a cup that are shaking about, and then assume the grains are less than a nanometer long. This is akin to what David Hume and colleagues from the University of Heidelberg in Germany have recently done [1]. As reported in Physical Review Letters, by observing the light emitted from a collection of laser-cooled and trapped atoms, they can distinguish two ensembles differing by just one atom—one grain—and directly observe a small step in signal when one atom is lost from the trap (Fig. 1). You might also wonder why anybody would want to count atoms to one thousand instead of being satisfied with distinguishing, say, one atom from two. The answer is that one day such particle counting techniques could extend precision quantum measurements well beyond current limits, helping to improve the accuracy of atomic clocks [2,3], or allowing an increase in the capability of atomic magnetometers.
The most sensitive measurements of various quantities such as time, magnetic field, or motion, are quantum measurements based on interference of waves. Such interferometers, whether they use light or massive particles such as atoms, now almost routinely reach precisions that are not dominated by any technical noise source, but by fluctuations that are inherently quantum mechanical in character. These fluctuations arise directly from the “quantumness” of nature—the granularity associated with particle number or discrete atomic energy levels. A well-known example is shot noise: if a measurement of the average power associated with a stream of photons is repeated multiple times with high resolution, the results will differ because photons arrive randomly. A similar effect limits atomic clocks and other matter-wave interferometers. In atomic clocks, a quantum phase that measures time is estimated by detecting the population difference between two atomic states. Consider an ensemble of atoms in which each atom has equal probability of being in one of two states. In this case, there is quantum noise associated with the distribution of possible measurement outcomes. The corresponding measurement limit, where precision improves as the square root of atom number , is called the standard quantum limit. So even with atoms, the best error you could hope for is atoms.
In principle, the standard quantum limit is not an absolute limit, in that it assumes that the atoms are independent of one another; i.e., it ignores the possibility of correlations between different atoms. Achieving such quantum correlations (known as entanglement) in large ensembles is difficult, as it requires a highly controlled interaction between the atoms. Nevertheless, experiments have begun to establish ways to overcome the standard quantum limit. There are two notable methods: The first is to redistribute (“squeeze”) quantum noise in such a way that it is reduced in the quantity that is being measured [4], a method referred to as spin squeezing [5–8]. The second method involves what are popularly called Schrödinger cat states—a superposition of states that are macroscopically so different that Austrian physicist Erwin Schrödinger compared the situation to a cat being simultaneously dead and alive. Such many-atom states can be set up so that the quantum-mechanical phase, which measures the signal of interest, for instance, time in an atomic clock, is much more sensitive to the quantity of interest than in a regular interferometer, thereby boosting the precision of the measurement. The ultimate performance is reached at the Heisenberg limit where precision improves linearly with atom number. Both methods for overcoming the standard quantum limit require a final-state readout with high resolution, well below the projection noise limit. In particular, the Heisenberg limit requires a readout with single-particle resolution, or, equivalently, the ability to distinguish an even number of atoms from an odd one.
Thus the capacity to count atoms one by one represents an enabling technique for future Heisenberg-limited measurements such as atomic clocks, magnetometers, or gyroscopes. A previous experiment reached single-atom resolution up to an atom number of but did not directly reveal discrete steps associated with the signal from individual atoms because of a spatially varying coupling to the measurement light field [9]. The present experiment by Hume et al. boosts the single-atom resolution by an order of magnitude, and clear steps in the signal associated with individual atoms are observed with ensembles containing over two hundred atoms.
To detect the atoms, the Heidelberg group optically traps and continuously laser cools the atoms, and collects the light scattered in the cooling process for atom detection. In order to achieve the necessary sensitivity, the researchers use high beam intensity—such that the atoms scatter light at almost the maximum possible rate—and image the atomic cloud onto a low-noise camera while carefully eliminating any stray light. Single-atom resolution requires the detection of many photons per atom: The detected photon number per atom must exceed the atom number; otherwise the photon shot noise thwarts the atom signal. The resolution therefore first improves with photon number and detection time but eventually decreases again as atoms become more and more likely to be randomly lost from the trap. With optimized detection time, typically milliseconds, single-atom resolution is attained for up to atoms in the present experiment.
Actually, measurements beyond the standard quantum limit require not only counting of the total atom number but also the selective counting of atoms in a specific internal state. The latter is more difficult as atoms may change internal state as they scatter light in the detection process, reducing the available detection time. In the Heidelberg experiment state-specific detection is achieved by pushing away atoms in the other hyperfine state with a resonant laser beam. State-specific single-atom resolution is attained for up to atoms, times smaller than for the counting of total atom number but larger than a previous limit of atoms [9]. The state-dependent detection could possibly be further improved in the future by separating the internal states spatially, e.g., with a magnetic field gradient, prior to optical detection with the camera.
The main task, however, is to combine this detection method with a setup that allows one to perform atom interferometry using entangled states, prepared, e.g., via collisions in a Bose-Einstein condensate [7,8] or via interaction with a light field [5,6]. Nonetheless, the rapid progress in entangling large ensembles made in the last few years [5–8,10] suggests that we will have precision clocks and atom interferometers operating substantially below the standard quantum limit in the not too distant future. With the current improvements in atom detection, even Heisenberg-limited measurements on moderate-size atomic ensembles appear quite within experimental reach.
References
- D. B. Hume, I. Stroescu, M. Joos, W. Muessel, H. Strobel, and M. K. Oberthaler, “Accurate Atom Counting in Mesoscopic Ensembles,” Phys. Rev. Lett. 111, 253001 (2013)
- N. Hinkley, J. A. Sherman, N. B. Phillips, M. Schioppo, N. D. Lemke, K. Beloy, M. Pizzocaro, C. W. Oates, and A. D. Ludlow, “An Atomic Clock with Instability,” Science 341, 1215 (2013)
- B. J. Bloom, T. L. Nicholson, J. R. Williams, S. L. Campbell, M. Bishof, X. Zhang, W. Zhang, S. L. Bromley, and J. Ye, “An Optical Lattice Clock with Accuracy and Stability at the Level,” arXiv:1309.1137 (2013)
- D. J. Wineland, J. J. Bollinger, W. M. Itano, F. L. Moore, and D. J. Heinzen, “Spin Squeezing and Reduced Quantum Noise in Spectroscopy,” Phys. Rev. A 46, R6797 (1992)
- J. Appel, P. J. Windpassinger, D. Oblak, U. B. Hoff, N. Kjærgaard, and E. S. Polzik, “Mesoscopic Atomic Entanglement for Precision Measurements Beyond the Standard Quantum Limit,” Proc. Natl. Acad. Sci. U.S.A. 106, 10960 (2009)
- I. D. Leroux, M. H. Schleier-Smith, and V. Vuletic, “Implementation of Cavity Squeezing of a Collective Atomic Spin,” Phys. Rev. Lett. 104, 073602 (2010)
- C. Gross, T. Zibold, E. Nicklas, J. Esteve, and M. K. Oberthaler, “Nonlinear Atom Interferometer Surpasses Classical Precision Limit,” Nature (London) 464, 1165 (2010)
- M. F. Riedel, P. Böhi, Y. Li, T. W. Hänsch, A. Sinatra, and P. Treutlein, “Atom-Chip-Based Generation of Entanglement for Quantum Metrology,” Nature (London) 464, 1170 (2010)
- H. Zhang, R. McConnell, S. Cuk, M. H. Schleier-Smith, I. D. Leroux, and V. Vuletic, “Collective State Measurement of Mesoscopic Ensembles with Single-Atom Resolution,” Phys. Rev. Lett. 109, 133603 (2012)
- J. Bohnet, K. C. Cox, M. A. Norcia, J. M. Weiner, Z. Chen, and J. K. Thompson, “Reduced Back-Action for Phase Sensitivity 10 Times Beyond the Standard Quantum Limit,” arXiv:1310.3177 (2013)