Little Earthquakes in the Lab
The 1970s heyday of earthquake research was characterized by a high degree of optimism, as leading scientists expressed hope that some method of predicting earthquakes might be around the corner. This was partly based on the assumption of a close similarity between seismic events and controlled indoor laboratory tests on the fracture of rock samples [1]. Such expectations led to the belief that diagnostic earthquake precursors (such as electromagnetic or acoustic phenomena, radon gas emissions, and the like) may be identified. This early optimism faltered as reliable precursors failed to materialize when subjected to rigorous statistical testing [2], and as results from theories of complexity [3] provided a possible physical explanation for their absence [4]: even fully deterministic systems of interacting elements can exhibit chaotic behavior, associated with an extreme sensitivity to initial conditions that makes accurate prediction impossible.
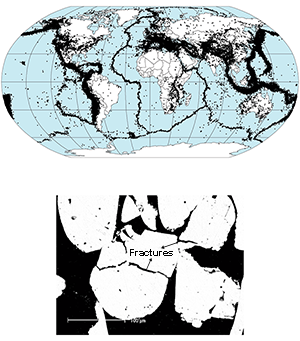
While the deterministic prediction of individual earthquakes with sufficient accuracy to justify an evacuation before an event is still considered to be beyond reach—and may not even be a realistic scientific goal [5]—probabilistic earthquake forecasting (i.e., the quantification of earthquake hazards in a given area and period of time) is instead enabled by the fact that earthquakes are not completely random events: they are localized, predominantly on plate boundaries (see Fig. 1), and tend to cluster in time [6].
Earthquake statistics obey a range of empirical scaling laws that help carry out seismic hazard analysis, set building design codes, or identify periods of elevated risk due to clustering. Such scaling laws may also provide strong constraints on the physics underlying the occurrence of earthquakes. Earthquake models are often built by scaling up constitutive rules derived from fracture and friction experiments in the laboratory, but an accurate statistical comparison between such lab tests and real earthquakes was lacking. Now, writing in Physical Review Letters, Jordi Barò at the University of Barcelona, Spain, and colleagues provide perhaps the most comprehensive statistical comparison to date between seismic events in the laboratory and in nature [7]. Their results show that, within an impressive range of several orders of magnitude, data collected from their laboratory-scale experiments and from earthquake databases collapse on the same distribution curves, revealing very similar scaling laws.
Ultimately, the clustering of earthquake probability distributions in space and time is due to a sensitive response to small fluctuations in local stress, consistent with a physical system that is close to criticality (e.g., at a first- or second-order phase transition), in which the failure of an element of the system can trigger that of another element that is close in space or time. This is analogous to the spread of a contagious disease in a population by local transmission of infection between a carrier and a healthy but susceptible individual. Based on this idea, statisticians have developed a purely stochastic earthquake model, called epidemic-type aftershock sequence (ETAS) that combines epidemic-type models for disease transmission with empirical scaling laws observed more or less ubiquitously in earthquake occurrence.
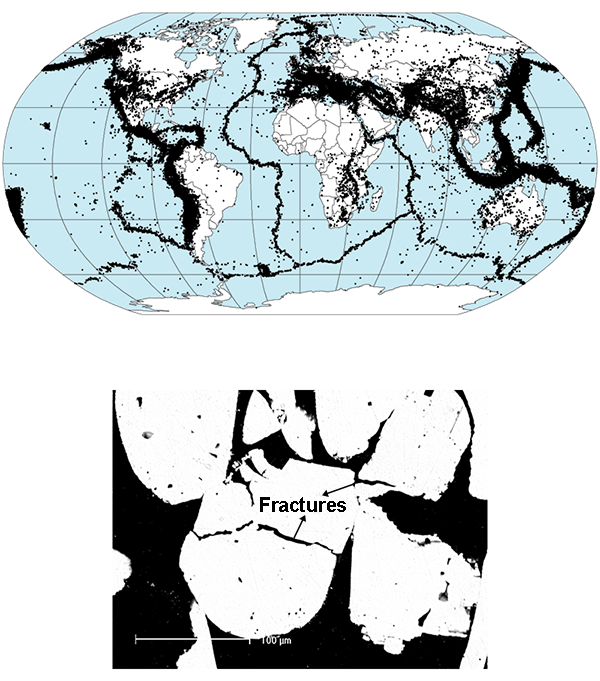
Three scaling laws have proven to be of very general validity. First, the Gutenberg-Richter law captures the fact that small earthquakes are more frequent than large earthquakes, providing a relationship between the magnitude and number of earthquakes in a given region. Second, the Omori law describes how the probability of aftershocks decreases with time: it is approximately inversely proportional to the time elapsed from the main shock (the largest in a sequence). Finally, the so-called “aftershock productivity” law relates the rate of aftershocks triggered by a mainshock to its magnitude: larger-magnitude earthquakes produce on average more aftershocks at a rate that depends on the local susceptibility to triggering [8]. All of these fundamental observations take the form of power-law distributions. The ETAS model combines these three laws with a random population of independent “background” events that trigger sequences of correlated events (whereby the correlation is caused by stress transfer—the equivalent of contagion in the spread of a disease). One of the key signatures of epidemic-type aftershock sequences is “crackling noise”: the kind of noise, arising from a combination of random cracking events and clusters of consequent events, that can be heard when sitting by a fire or crunching a piece of paper. Crackling noise has been shown to accompany both earthquakes and the formation of microcracks in laboratory tests on the fracture of granular or composite media (see Fig. 1).
Within the ETAS stochastic modeling framework, Barò et al. compare new experimental work on compaction tests in a granular medium with the analysis of an earthquake catalog (a table of time, magnitude, and location of earthquake events). The experiments involved subjecting a high-porosity silica ceramic (a simple synthetic sedimentary “rock”) to a uniaxial compression that increases linearly until the sample fragments into pieces. Simultaneously, the mechanical response of the sample was monitored by detecting high-frequency elastic waves resulting from internal microcracks and analyzing them in exactly the same way as real earthquake data. The results show that the Gutenberg-Richter law holds over – orders of magnitude, which, in itself, is an impressive achievement in terms of experimental sensitivity. At the same time, when properly normalized, data obtained under different compression rates collapse onto a single curve, signaling universal scaling laws that follow both the Omori law and the related aftershock productivity law. Despite the great differences in spatial and temporal scales, the external boundary conditions, and the significantly different material properties of the media involved, the authors find that the three scaling laws of seismicity hold their validity in the laboratory experiments, with only a slight difference in the precise scaling exponents with respect to the earthquake case.
The authors further deepen the comparison by analyzing the distribution of waiting times between consecutive events. The analysis confirms a remarkable similarity in the scaling behavior of waiting time probabilities previously attributed to the ETAS behavior [9,10], but it also shows something fundamentally new, which will have to be considered in future earthquake modeling. Rather than a single power law with an exponential tail (gamma-type distribution), the distributions are best fitted by the combination of two power laws. In a double-logarithmic plot, this appears as a “dog-leg” distribution: a curve made of two segments with different slope, resembling the hind leg of a dog. Under stationary conditions, the ETAS model produces a gamma distribution resulting from a mixing of random background events and correlated aftershocks [9,10]. Barò et al. demonstrate that the dog-leg law is instead due to nonstationarity in the rate of background events. They argue that the origin of nonstationarity is different in the two cases: in space (for earthquakes) and in time (for the lab experiment). In the lab experiment this is attributed to a nonlinear acceleration in background rate as the stress is increased in time. For earthquakes, nonstationarity is most likely due to variability in background rate associated with spatial clustering.
Future experiments will need to address some outstanding issues, in particular, realizing conditions that are closer to those relevant for earthquakes. The seismogenic part of the Earth’s lithosphere deforms under triaxial, rather than uniaxial, compression, doesn’t have well-defined boundaries, and is much more heterogeneous and less porous than the simple synthetic rock investigated. As a consequence, in Barò et al.’s lab experiments, a large amount of strain is likely to be accommodated by nonseismic mechanisms associated with the slow closing of pores. It will also be interesting to carry out spatially resolved experiments to locate the sources of the acoustic emission events, in order to disentangle the relative contributions of spatial and temporal variability to the nonstationarity highlighted by the authors’ experiments.
The results of Barò et al. certainly boost the confidence that the ETAS model can tackle seismology problems at all scales, from earthquakes to the deformation of porous granular media, and may help develop better probabilistic forecasting models for earthquakes and other natural hazards such as landslides and forest fires. However, only extensive testing with future observations will reveal the true forecasting power of this approach and the extent to which it could provide guidance for policies and operational decisions [11].
References
- C. H. Scholz, L. R. Sykes, and Y. P. Aggarwal, “Earthquake Prediction: A Physical Basis,” Science 181, 803 (1973)
- S. Hough, Predicting the Unpredictable: The Tumultuous Science of Earthquake Prediction (Princeton University Press, Princeton, 2009)[Amazon][WorldCat]
- P. Bak, How Nature Works: The Science of Self-Organised Criticality (Oxford University Press, Oxford, 1997)[Amazon][WorldCat]
- I. Main, “Statistical Physics, Seismogenesis, and Seismic Hazard,” Rev. Geophys. 34, 433 (1996)
- http://www.nature.com/nature/debates/earthquake/equake_frameset.html
- M. Huc and I. G. Main, “Anomalous Stress Diffusion in Earthquake Triggering: Correlation Length, Time Dependence, and Directionality,” J. Geophys. Res. 108, 2324 (2003)
- J. Baró, Á. Corral, X. Illa, A. Planes, E. K. H. Salje, W. Schranz, D. E. Soto-Parra, and E. Vives, “Statistical Similarity between the Compression of a Porous Material and Earthquakes,” Phys. Rev. Lett. 110, 088702 (2013)
- Y. Ogata, “Statistical Models for Earthquake Occurrences and Residual Analysis for Point Processes,” J. Am. Stat. Assoc. 83, 9 (1988)
- A. Saichev and D. Sornette, “Theory of Earthquake Recurrence Times,” J. Geophys. Res. 112, B04313 (2007)
- S. Touati, M. Naylor, and I. G. Main, “The Origin and Non-Universality of the Earthquake Inter-Event Time Distribution,” Phys. Rev. Lett. 102, 168501 (2009)
- T. Jordan, Y. Chen, P. Gasparini, R. Madariaga, I. Main, W. Marzocchi, G. Papadopoulos, G. Sobolev, K. Yamaoka, and J. Zschau, “Operational Earthquake Forecasting: State of Knowledge and Guidelines for Utilization,” Ann. Geophys. 54, 361 (2011)